浅谈不定积分运算中的灵活性

蒋志荣

（肇庆科技职业技术学院，广东 肇庆 526020）

浅谈不定积分运算中的灵活性

蒋志荣

（肇庆科技职业技术学院，广东 肇庆 526020）

求不定积分的过程比较复杂，没有一个统一的法则可以遵循。本文就不定积分运算中的一些灵活技巧给予了诠释。

不定积分；换元法；分部积分法；凑微分法

下面仅就不定积分运算中的一些灵活技巧给予诠释。

例1

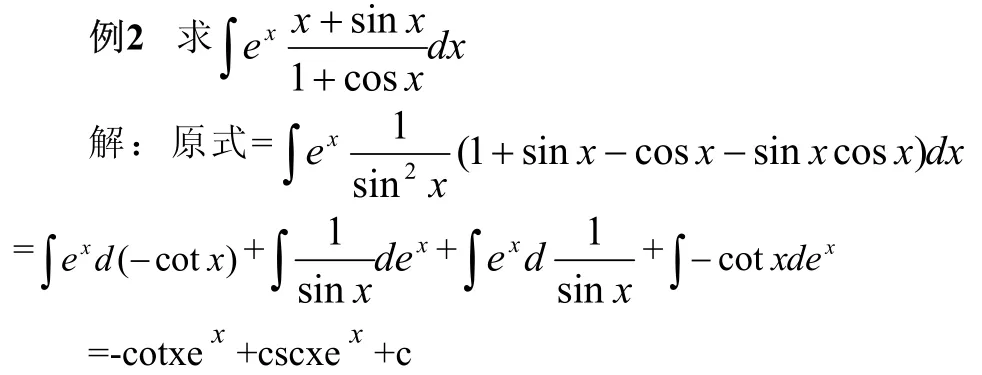
本题不仅利用了公式duvudv∫∫+= uv+c，同时在三角函数有理式处先使分母出现平方项，再化简，这也是种有效的方法。

在此例中利用了使分母出现平方项再化简的方法，从而使问题得以简化，当然有些问题直接利用第一，二换元法也可。

本例关键利用第二换元法 tx sin= 同时将 tcos用代换，从而使问题迎刃而解。可见代换也是求不定积分比较常用的一种方法。

本例采用分子，分母同乘以 ex，从而可凑微一般情况下，当被积函数含有 ex时，上述凑微分法也是比较常见的。

在不定积分运算中，不仅方法是多样的，而且灵活性也较强。那么在实际运算中究竟采用哪种方法，还要因题而宜。通过多做习题来不断积累经验，以求在掌握各种方法同时，灵活地运用它们。

[1] 李晓主编. 高等数学[M]. 浙江大学出版社.

[2] 李心灿主编. 高等数学[M]. 高等教育出版社.

O174

A

1008-7427（2011）03-0160-01

2010-12-24