基于神经网络的高校教师课堂教学质量评价

左国平 谢红艳 邱小平 于 涛 宋碧英

南华大学 湖南衡阳 421001

基于神经网络的高校教师课堂教学质量评价

左国平 谢红艳 邱小平 于 涛 宋碧英

南华大学 湖南衡阳 421001

在分析了高校教师教学质量评价特点的基础上，构建了一种基于模糊理论与神经网络的高校教师教学质量评价体系。该模型将教学评价指标概念量化成确定的数据作为网络的输入，模糊综合评价结果作为输出。该方法既克服了评价主体在评价过程中的主观因素，又得到了满意的评价结果，具有广泛的适用性。

模糊理论；神经网络；教学质量；评价

教学质量是教育的生命线，是高等院校能否持续健康发展的关键所在。长期以来教学质量的评估多是采用直接建立评价系统的数学模型，如：层次分析法、模糊综合评判法、灰色系统、聚类分析等。这些方法能充分考虑各种评估因素并体现专家经验知识，但这些方法在评估过程中难以排除各种随机性和主观性，忽视了各评价指标和教学效果之间的非线性关系，其结果带有很大的主观性，难以真实反映教学质量状况。

人工神经网络是信息科学与技术研究领域中一门新兴学科，它是基于模仿人类大脑的结构和功能而构成的一种信息处理系统，神经网络以其自有的模拟人的思维、非线性变换和自学习等功能，充分克服了上述缺陷，是进行教学质量评估的有效方法。

1 教学质量评估指标体系的建立

影响教师课堂教学质量的因素有很多，建立科学合理的评价指标体系是进行科学评价的前提，评价指标的建立必须遵循一定的原则，使建立的指标体系更加合理、更具有说服力。一般来说，指标设置应遵循5项原则：

(1)科学性原则。指标设置要客观地反映分析对象本身的性质、特点、内在关系和变动过程。对于课堂教学评价，指标体系反映的应该是课堂教学质量的内涵要求。

(2)全面性原则。应尽可能从各个角度反映对象的全貌，防止以偏概全。同时，抓住重点，防止因小失大。要从全局出发，建立完整的评价指标体系，以利于评价结果的公正性和权威性。建立的指标体系应能综合反映对象各方面的特性。

(3)独立性原则。同一层次的各指标应能各自说明被评价对象的某一方面，指标间不互相重叠，不存在因果关系。

(4)可行性原则。应尽可能利用统计系统公开的统计数据，保证评价的可操作性和公开性，提高指标体系在实际工作中执行和应用的可行性。

(5)以人为本原则。高校要提高教学质量，就要充分利用人力资源，使他们在教学中发挥出尽可能大的作用。因此，课堂教学质量评价应体现重视人、尊重人、爱护人、激励人的思想，在指标体系的设计上也应体现这一思想。

根据上述原则结合笔者所在高校的具体情况，课堂教学水平质量评价可以通过教学素质、教学态度、教学内容、教学效果和教学方法手段等一级指标进行。为了使评价指标更具有可操作性，可以将这些一级指标细化为更具体的二级指标(见表1)。

表1 教学质量评价指标体系

根据以上分析，制成调查表，通过教学质量调查活动，对笔者所在学院2007级、2008级学生开展调查活动，得到482份有效调查结果，将调查结果进行预处理，得到训练样本（见表2）。将样本数据的2/3用于训练网络，1/3的数据用于网络检测，期望输出可采用专家组对该课程的评价结果。

表2 教学质量调查评估结果

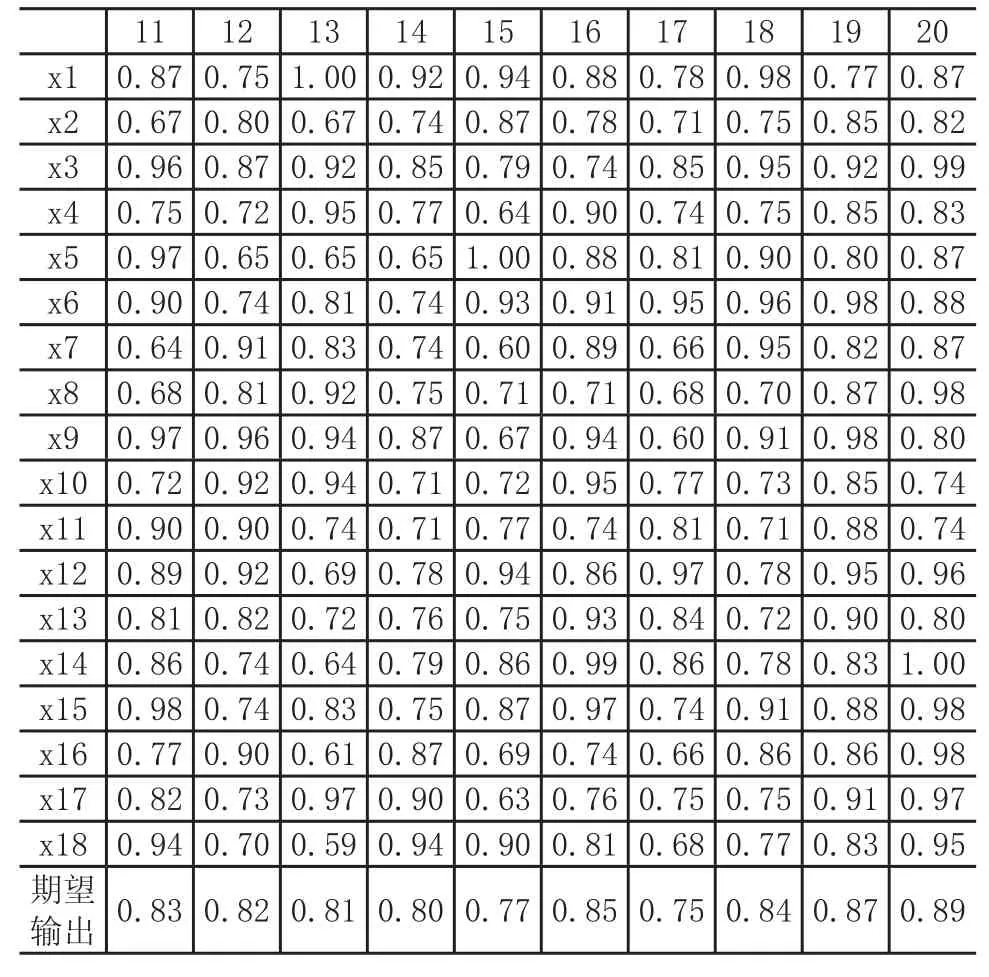
续表2

2 基于BP神经网络的教学质量评估模型

BP算法是为了解决多层前馈神经网络的权系数优化而提出来的，是目前应用最广泛的神经网络学习算法之一。BP网络学习过程由信号的正向传播与误差的反向传播两个过程组成。

BP网络的学习过程可分成4个步骤，即模式顺传播→误差逆传播→记忆训练→学习收敛。此过程一直训练到网络输出的误差减少到可以接受的程度，或进行到预先设定的学习次数为止，最终以系统的输出作为评价的目标。为了使模型具有理论价值又有可操作性，根据实际情况我们构建如下的神经网络模型：

(1)输入层神经元个数的确定。根据指标体系，影响教学质量的主要指标有18项，因此取输入层神经元个数n=18，由于输入数据是离散型的数值量，把它们归一化后作为输入量。

(2)输出层神经元个数的确定。评价结果作网络的输出，因此取输出层个数m=1，并把输出数据归一化后作为输出量。

(3)网络隐含层数的确定。隐含层数越多，神经网络学习速度就越慢，根据Kosmogorov定理，在合理的结构和恰当的权值条件下，3层BP网络可以逼近任意的连续函数，因此，我们选取结构相对简单的3层BP网络。

(4)隐含层神经元个数的确定。隐含层神经元数的选取关系到整个BP网络的精确度和学习效率，最佳隐节点数可参考公式计算：

n为输入节点数，m为输出节点数，α为介于1～10的常数。本文的输入神经元为18个，输出为1个，所以隐含层神经元为5～14个。经过反复试验，得到最佳隐层节点数为10个。

(5)转换函数的确定。BP神经网络神经元转换函数，可采用S型函数，函数形式为：

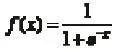
通过以上分析得到如图1所示的BP网络拓扑结构。

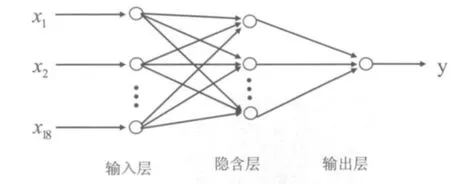
图1 教学质量评价的模糊神经网络模型结构

3 网络模型的实现

根据模型，利用Matlab对其进行仿真，可得网络建立过程的误差曲线，如图2所示。

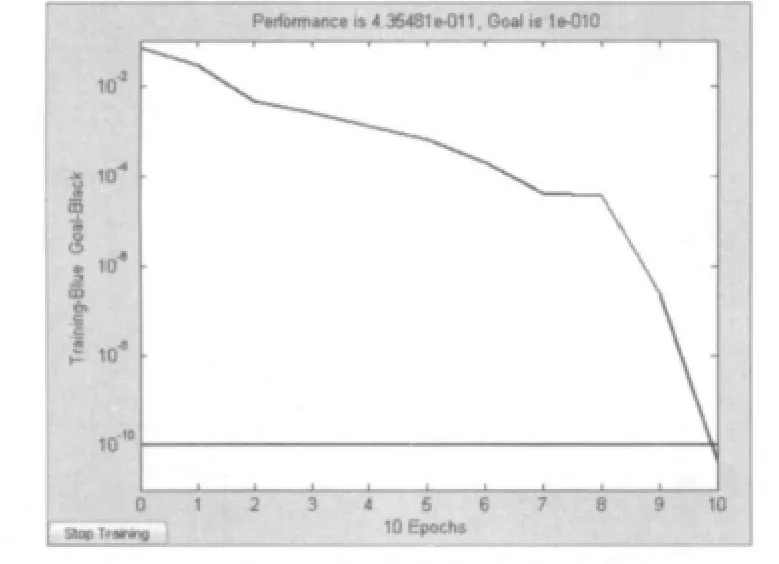
图2 训练误差曲线

可以看出，神经网络经过10步迭代即达到精度要求，训练时间很短。训练后的结果如图3所示，训练值与目标值符合得很好。

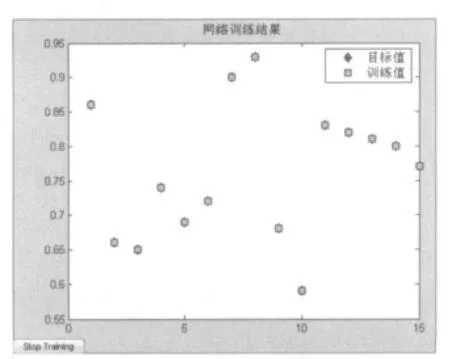
图3 网络训练结果

为了检测网络的泛化能力，对后5个样本数据进行了预测，预测结果及相对误差见表3。

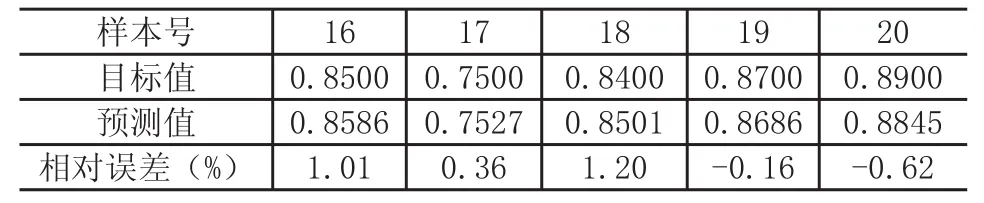
表3 检测样本的预测结果

通过Matlab的运行结果，对照表2可知该网络组的状态分类器可以有效准确地识别该教学质量评估的情况。这与实际情况是相符合的，说明设计的教学质量评估分类器是合理的，可以投入实际使用。

[1]汤小凝.模糊理论在高校教学质量评估中的应用[J].中国教育技术装备，2008，8：6～8

[2]仁善强，雷鸣.数学模型[M].重庆：重庆大学出版社，1998

[3]刘敏慧.层次分析法在高职院校教师教学质量评价中的应用[J].天津职业大学学报，2008，17(6)：26～28

[4]闻新，周露.Matlab神经网络应用设计[M].北京：科学出版社，2000

[5]刘杰.构建研究型大学课程教学质量评价指标体系的探讨与实践[J].高等理科教育，2003，6：1～6，11

[6]黄关扬.教育测量与评价[M].上海：华东师范大学出版社，2002

Abstract: Based on the analysis of features of teaching quality appraisal of teacher sin colleges and universities, an evaluation model of university teachers’ teaching quality based on fuzzy theory and BP neural network is introduced. The model transforms teaching evaluation indicators into qualified data as BP network input and takes fuzzy synthetic evaluation results as output. the method can both overcome the subjective factors of evaluation main body in evaluation process and bring the satisfactory evaluating results，and it has the widespread serviceability.

Key words: fuzzy theory; neural network; teaching quality; evaluation

Using neural network to evaluate university teachers' teaching quality

Zuo Guoping, Xie Hongyan, Qiu Xiaoping, Yu Tao, Song Biying
University of south China, Hengyang, 421001, China

2010-09-10

左国平，硕士，讲师。通讯作者：谢红艳，硕士，讲师。

湖南省普通高等学校教学改革项目，南华大学高等教育与改革课题（编号：2009ZZ061），南华大学高等教育与改革课题（编号：2009PP027）。