基于EKF的两台五相PMSM串联系统研究

苗正戈，刘学忠，刘陵顺，张海洋

（1.海军航空工程学院 控制工程系，山东 烟台 264001；2.国核电力规划设计研究院 北京 100094）

单逆变器驱动定子串联联接的两台五相PMSM新型多电机驱动系统，因而这种新型多电机驱动系统可以节省控制装置器件数量，降低系统成本，其新颖之处是采用一套DSP平台同时控制多台串联联接的多台电机，在同一逆变器供电条件下，实现多台电机的解耦控制。在对两台串联PMSM进行控制时，需要知道转子转速及位置，传统方式是采用高精度、高分辨率的速度和位置传感器（例如光电编码器等），这些传感器大都价格昂贵，不仅提高了系统的成本，还限制了设备在恶劣环境下的应用。运用无速度传感器控制技术，可以在线估计电机的速度和位置，从而省去了传感器。目前的估计方法分两类：一类是基于电机非理想特性的方法，应用较多的有高频信号注入法等，这类方法在低速和零速附近具有一定的优势，但是高频信号注入法会产生转矩脉动和附加损耗、噪音等问题。另外一类是基于电机理想电压方程的方法，如反电势计算法、模型参考自适应法、Romberg状态观测器、扩展Kalman滤波器（EKF）等，在这类方法中，相对于反电势计算法等开环估计方法，Romberg观测器和EKF由于有闭环校正环节，其观测精度和稳定性都相对较高。由于永磁同步电机方程为非线性方程，而EKF是基于最优化理论的针对非线性模型的观测器实现方法，因此在永磁同步电机中具有很大的优势。本文在转子磁链定向的同步旋转坐标系下采用基于EKF的状态观测器来观测两台串联电机的转子位置和转速，并实现了两台串联电机无机械传感器解耦矢量控制[1]。

1 两电机串联驱动系统

1.1 两台五相PMSM串联联接定子绕组连接关系

两电机定子绕组串联关系见图1，两台五相PMSM各相绕组间的夹角为α1=α2=2π/5，通过这种联接，电机2的磁通和力矩电流分量（αβ电流分量）将不在电机1中产生磁通和力矩（作为电机1的xy电流分量），而电机1的磁通和力矩电流分量在与电机2的联结点位置相加为零值，因此，这就实现了两台电机在同一逆变器下的独立解耦控制。

1.2 两台五相PMSM原理及数学模型

根据多相电路坐标变换的一般理论，在对两台五相PMSM串联研究分析时需要用到矢量空间变换矩阵

图1 两台PMSM串联图Fig.1 Two motor connection diagram

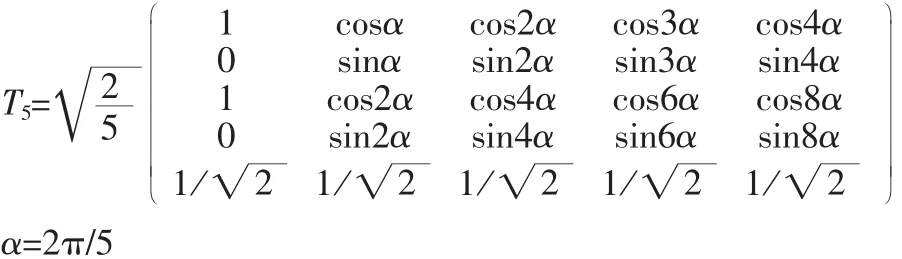
通过变换将控制五相PMSM需要的电流或电压等实际物理量变换到V1平面，将控制第二台五相PMSM需要的实际物理量变换到V2平面。文献[2]中已经证明V1、V2相互正交，所以可以实现两台五相PMSM解耦控制。

两电机串联模型如下：

五相PMSM数学模型

第二台五相PMSM数学模型：

2 两台五相PMSM无速度传感器控制系统

两台五相PMSM无速度传感器结构图如图2所示。

扩展卡尔曼滤波算法则是线性卡尔曼滤波器在非线性系统中的推广与应用。卡尔曼滤波的基本思想是把不可观测的待估计的状态变量x看做随机变量，它与观测得到输入输出变量是密切相关的，卡尔曼滤波正是基于这些可观测的输入输出变量去推断那些不可观测的状态变量。

一般的非线性系统状态方程为：

图2 两电机串联系统无速度传感器控制系统结构图Fig.2 Control system of two motor connect in series based on EKF

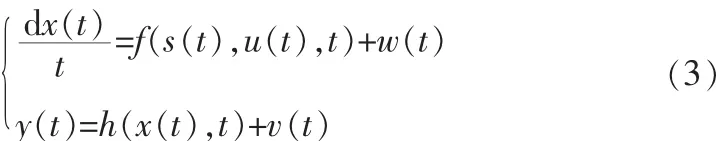
式中，x （t）是系统状态变量，u （t）是系统输入量，y （t）是系统输出量，在估计的过程中，w（t）设为系统随机噪声，它包含输入扰动和系统模型偏差；m（t）为测量随机噪声。假设w（t）、m（t）均为正态噪声，且均值为零互不相关。w（t）和 m（t）的协方差矩阵分别为Q和R，并且Q和R是对角矩阵，其余元素为零。

从两台五相PMSM驱动控制系统模型得出，单台多相电机的无速度传感器控制技术能够很好地拓展到两台五相PMSM串联驱动控制系统中，对于单台多相电机而言，建立基于EKF的电机模型，需要逆变器输出电压和电流的d-q分量；而对于两台五相PMSM，则需要用x-y分量控制第二台电机。

图2中，逆变器电压和电流的d-q分量作为电机1的EKF估计器输入，与之类似逆变器电压和电流的x-y分量则作为电机2的EKF估计器输入。

选取状态变量：

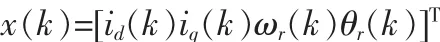
对于第一台电机系统状态方程可以表示为：

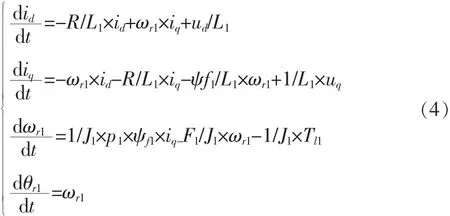
输出方程：

对系统进行离散化得：

状态方程：

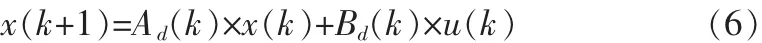
输出方程：

其中，

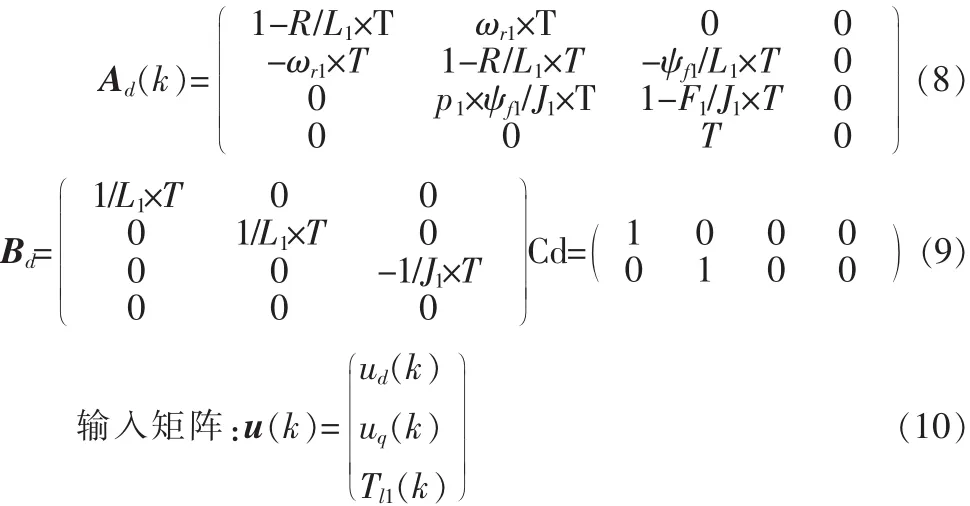
由于两台五相串联电机方程在形式上类似，所以只需要对电机1的无速度传感器模型中的相应变量作下修改即可，不再赘述。通过迭代并选取两电机的初始值如下[4-6]：

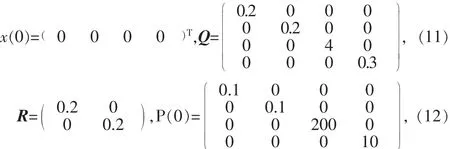
电机参数设置如下：

第一台电机，L1=8.5 mH，p1=6，R=2.875 Ω，J1=0.089，F1=0.005，ψf1=0.175 Wb，Tl1=0。

第 二 台 电 机 ，L2=9.2 mH，p2=6，J2=0.1，F2=0.01，ψf2=0.2 Wb，Tl2=0。

在Matlab/simulink中对s-function模块编程，将仿真条件设为，电机1在整个仿真过程中保持转速为300 r/min不变，电机2的初始速度设为200 r/min，在t=0.6 s时，电机反转，速度为100 r/min。在这种工作情况下，系统工作状况如图3、4所示。

通过图3和图4可以看出，在电机串联系统中应用基于EKF的无速度传感器技术能很好地估计相应的状态量，在系统转速发生变化时，采用无传感器控制算法后控制过程的上升时间较有传感器控制稍长一些，但仍能满足控制系统的性能指标要求。所以无论在稳态还是瞬时条件下估计转速和估计角位置对实测转速和实测角位置跟踪特性都很好。同样，旋转坐标系下q轴电流估计值能很好地跟踪其实际值。

通过图5，可以看出，电机2转速的变化，对电机1的转矩没有任何影响，从而说明基于EKF的无速度传感器技术可以应用于该串联系统的解耦控制中。

图3 两电机串联系统中第一台五相PMSM EKF仿真波形Fig.3 First five-phase PMSM EKF simulation waveforms

图4 两电机串联系统中第二台五相PMSM EKF仿真波形Fig.4 The Second five-phase PMSM EKF simulation waveforms

3 结 论

文中提出的将扩展卡尔曼滤波算法有效地应用于两台五相PMSM串联驱动系统中，具有估计精度较高、恶劣环境下可靠性高、成本低廉等优点，克服了应用传感器带来的困难，这种方法计算过程简单、直接，并且有迭代运算的特点，因此适合电子计算机在线估计。同时通过仿真实验可以得出把扩展卡尔曼滤波器应用于两台PMSM串联系统是可行的。

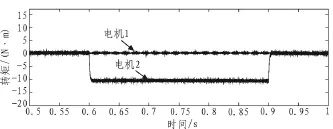
图5 两串联电机转矩波形Fig.5 Two series motor torque waveform

[1]郑泽东，李永东，Maurice FADEL.基于EKF的PMSM无机械传感器矢量控制[J]，清华大学学报：自然科学版，2009，49（10）:1585-1588.

ZHENG Ze-dong， LIYong-dong， FADEL M.PMSM mechanical sensor-less vector control based on extented Kalman filter[J].J Tsinghua Univ：Sci&Tec，2009， 49 （10）:1585-1588.

[2]陈菊明，刘锋，梅生伟，等.多相电路坐标变换的一般理论[J].电工电能新技术，2006， 25（1）：44-48.

CHEN Ju-ming， LIU Feng， MEISheng-wei， etal.Generalized coordinates transformation theory of multiphase system[J].Advanced Technology of Electrical Engineering and Energy， 2006， 25（1）:44-48.

[3]Martin J， Slobodan N V， Emil L.A novel aix-phase seriesconnected two-motor drive with decoupled dynamic control[C]//IEEE Ind.Appl.Soc.Annual Meeting IAS， Seattle，WA，2004:639-646.

[4]Khan MR，Iqbal A.Extended Kalman filter based speeds estimation of series-connected five-phase two-motor drive system[J].Simulation Modelling Practice and Theory，2009，17:1346-1360.

[5]Soltani J， Abjadi N R， ArabMarka-deh G R.Adaptive sliding-mode control of a two five-phase series-connected induction motors drive[C]//Proceeding.International Conference on Electrical Machines and Systems， Seoul， 2007，1496-1501.

[6]Djahbar A， Mazari B，Mansour N.A novel concept for multimachine drive aystems qith rotor time constant estimation[C]//International Multi-Conference on Systems，Signals and Devices，2008:1081-1085.