应用回归正交试验优化水杨酸异戊酯香料合成工艺条件

刘 峥，刘宝玉，陈世亮，王国瑞，莫秋生

（桂林理工大学 化学与生物工程学院，广西 桂林 541004）

应用回归正交试验优化水杨酸异戊酯香料合成工艺条件

刘 峥*，刘宝玉，陈世亮，王国瑞，莫秋生

（桂林理工大学 化学与生物工程学院，广西 桂林 541004）

利用一次回归正交试验分析法，对固体超强酸SO42-/TiO2-Nd2O3催化水杨酸异戊酯的工艺条件进行了优化建模，找出了主次影响因素，得到了酯化率与影响因素的回归方程，并对其进行验证。同时用其指导工艺的改进，结果表明采用一次回归正交试验分析法得到回归方程可以较好的预测该工艺体系中的酯化率，指导工艺改进。

水杨酸异戊酯；固体超强酸；回归正交试验；工艺优化

近二三十年来回归正交设计方法在有机合成反应研究中得到了广泛应用[1],它摆脱了古典回归分析的被动局面,把试验的安排、数据的处理和回归方程的精度统一起来考虑，使在每个试验点上获得的数据含有最大的信息，从而减少试验次数，而且使数据的统计分析具有一些好的性质[2]。实践表明回归正交设计方法在优化反应条件和产品配方优点显著[3-7]。

固体超强酸催化剂是近年来迅速发展的具有工业重大应用价值的新型催化剂,在酯化反应中显示出良好的催化活性, 因此,不断优化固体超强酸催化酯化反应的工艺条件成为重要的研究课题。对固体超强酸催化剂合成水杨酸异戊酯前人已经做了大量的工作，大多数研究的重点是固体超强酸催化剂的制备方法，对酯化工艺条件的研究大多建立在单因素方法的基础上，未见有SO42-/TiO2-Nd2O3催化剂催化合成水杨酸异戊酯及回归正交设计方法优化其工艺条件的报道。本文制备固体超强酸催化剂SO42-/TiO2-Nd2O3，着重利用回归正交设计方法[8]研究固体超强酸催化剂催化合成水杨酸异戊酯的数学建模及回归方程，利用回归方程找到最佳工艺条件[9]。

1 实验部分

1.1 主要试剂和仪器

异戊醇（ AR）广东汕头市西陇化工厂；氧化钕（AR）国药集团化学试剂有限公司；GS28-B型电子调速搅拌器 上海安亭电子仪器厂；DF-101S集热恒温加热磁力搅拌器 郑州长城科工贸有限公司； DZF-6020型真空干燥箱 上海一恒科技有限公司；SHB-Ⅲ型循环水式多用真空泵 郑州长城科工贸有限公司；SX2 5-1型马弗炉 上海沪越实验仪器有限公司；WZS-1 790099型阿贝折光仪 上海赤天公司。

1.2 实验方法

1.2.1 稀土复合固体超强酸 S O42-/TiO2-Nd2O3催化剂的制备

用2.0 mol/L稀H2SO4溶液将0.21 g Nd2O3刚好溶解, 再加入硫酸钛，并加水充分溶解。在搅拌下缓慢滴入28%氨水，直至溶液pH达到9.0～10.0之间，再搅拌10 min左右，静止陈化24 h，抽滤，所得沉淀依次用蒸馏水、乙醇充分洗涤，然后在105～110℃烘箱中干燥24 h。沉淀磨细后，从中称取10 g，用0.5 mol/L的H2SO4溶液浸泡15 min，抽滤，红外灯下干燥、研磨成粉体，最后在马弗炉中于600 ℃焙烧 3 h，即可制得稀土复合固体超强酸SO42-/TiO2-Nd2O3催化剂，放入干燥器中备用[10]。

1.2.2 水杨酸异戊酯合成方法

用电子天平准确称取 6.9 g水杨酸和 0.98 g SO42-/TiO2-Nd2O3催化剂，倒入50 mL的三口烧瓶中，量取2.8 mL异戊醇，倒入三口烧瓶，插好温度计和分水器（分水器中装满异戊醇），接好回流冷凝管，加热分水回流，至再没有水分出为止，自然冷却至室温。将反应液倒入分液漏斗中，加入足量的碳酸氢钠饱和溶液中和未反应的酸，静置,分层后将有机层转入25 mL烧瓶中，先常温下加热，蒸出未反应的异戊醇，再减压蒸馏，收集160～200 ℃/100 kPa的馏分，即得到水杨酸异戊酯产品。按下式计算酯化率[11]：

酯化率= (1-反应某时刻酸值/反应初始酸值)×100%= (1-Vt/V0) ×100%

式中：V0、Vt分别表示反应初始时和反应t时刻取样滴定所消耗标准0.1 mol/L NaOH乙醇溶液的体积。

2 结果与讨论

2.1 一次回归正交试验方案和试验结果

影响酯化反应的因素很多，但最主要的因素是反应时间、催化剂用量、酸醇摩尔比。因此，本文采作三因素二水平回归正交设计方法进行优化，以酯化率为指标，建立指标与各因素的回归方程（模型）。在探索性试验的基础上，确定了三因素的取值范围，因x1= 1～4 h，所以其上水平x12= 4,下水平x11= 1,零水平 x10= (x11+x12)/2 = (1+4)/2 = 2.5，变化间距△1= x12- x10= 4 - 2.5 = 1.5，z11= (x11-x10)/△1=(1-2.5)/1.5= -1。z2、z3的编码与z1类似，其结果见表1。

表1 因素水平编码表Table 1 Factor level coding table

按1次回归正交表L8（27）设计实验，将 z1、z2、z3分别安排在1，2，4列，第3列、5列和第6列分别为交互作用z1z2、z1z3和z2z3列。不进行零水平试验，故零水平试验次数m0= 0,总试验次数n = mc=8,试验方案和试验结果见表2。

表2 一次回归正交试验方案和试验结果Table 2 One regression orthogonal experiment and the experimental results

2.2 数据处理

2.2.1 回归方程的建立

将表2试验数据输入计算机用Microsoft Excel软件处理，得出回归方程为：

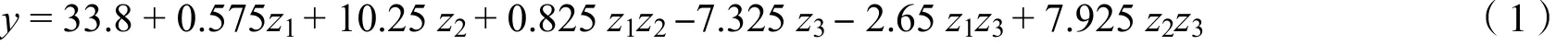
即回归系数：a = 33.8, b1= 0.575, b2= 10.25, b3= -7.325, b12= 0.825, b13= -2.65, b23= 7.925

根据回归方程中回归系数绝对值的大小，可以得到各因数和交互作用对指标影响的主次顺序为：

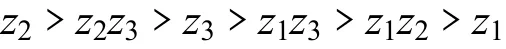
2.2.2 回归方程F检验

线性回归方差分析结果见表3。

由表3可以看出，式（1）回归方程线性显著，即酯化率与所讨论的3个因数之间有显著的线性关系。

表3 线性回归方差分析Table 3 Linear regression variance analysis

2.2.3 回归方程的复相关系数检验

由于SST= 1 903.74，SSR= 1 836.46，所以：

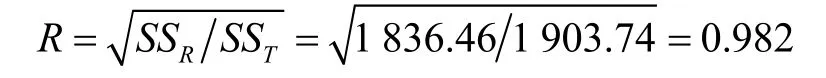
对于给定的显著性水平α = 0.05，自变量个数m = 3，试验次数n = 8时，查相关系数r与R的临界值表得对应的临界值Rmin= 0.912，故（1）式回归方程与试验数据拟合的很好，这与F检验的结论是一致的。

2.2.4 回归方程的偏回归系数的显著性检验

将表2实验数据进行方差分析，得表4。查得临界值F0.05(1,4) = 7.71，所以对于给定的显著性水平α=0.05，因数B，C和交互作用B×C对试验结果都有显著的影响。从表4中的F值的大小可以看出因素的主次顺序为B，B×C，C，这与表2中的极差分析结果是一致的。

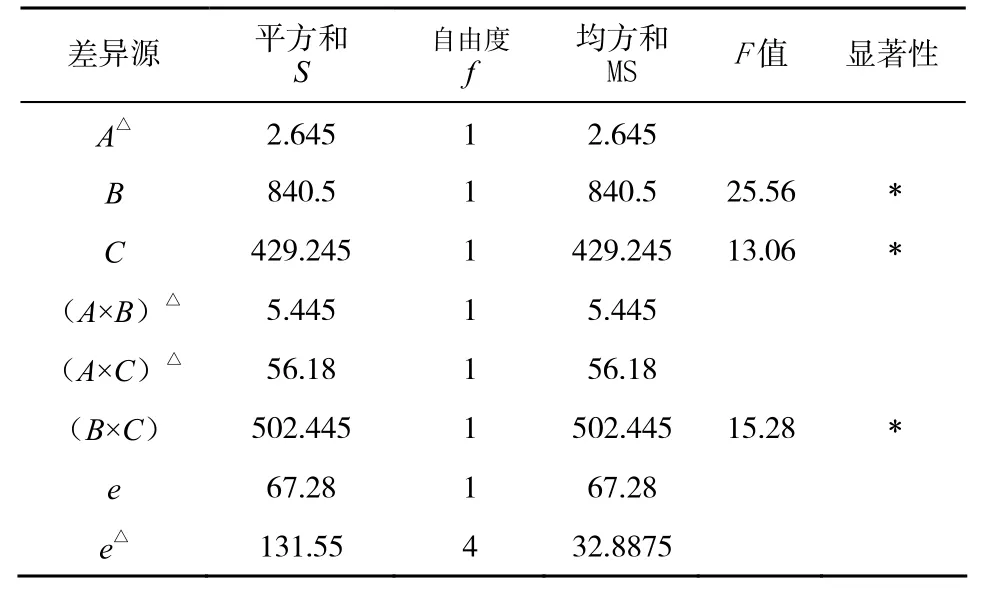
差异源 平方和S自由度f均方和MS F值 显著性A△ 2.645 1 2.645 B 840.5 1 840.5 25.56 ﹡C 429.245 1 429.245 13.06 ﹡（A×B）△ 5.445 1 5.445（A×C）△ 56.18 1 56.18（B×C） 502.445 1 502.445 15.28 ﹡e 67.28 1 67.28 e△ 131.55 4 32.8875

2.2.5 回归方程的回代

根据编码公式 z1=(x1-x10)/△1、z2= (x2-x20)/△2、z3= (x3-x30)/△3,将编码公式代入回归方程(1)式为：

方程简化为：

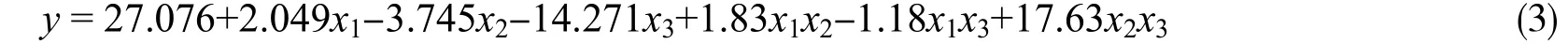
2.2.6 最优工艺条件的确定

酯化反应的最优工艺条件可由下列 2种方法确定。

方法1：在本试验中所讨论的指标酯化率越大越好，B、C、B×C的影响都是显著的，应选择[bc]ij([bc]ij表示Bi与Cj的水平组合对试验结果的联合效应，也称总效应，它等于Bi与Cj搭配条件下的酯化率的均值与总均值之差)中最大者对应的因数B、C的水平为优水平组合，根据表2中的数据列出了因数B、C的二元表（表5）。

由公式[ab]ij= Dijr2/n - T/n[12]，选[ab]ij中最大者只需选表5中BiCj中最大者，它所对应的因素B、C的最优水平搭配为B1C-1。由于A不是显著因素，故比较 A-1B1C-1，A1B1C-1，知最优水平组合为A-1B1C-1，即是表2中的第3号试验方案。

表5 因素B、C的二元表Table 5 Factors B, C of the binary table

方法2：所需酯化率在反应时间不超过4 h,催化剂用量不超过1.5 g, 醇酸摩尔比不超过4的条件下对方程（3）进行规划求解[13]。当x1= 4, x2= 1.5, x3=4时，y取最大值70.5%。根据模型条件，做3组平行实验。实验条件为：水杨酸10.6 g，异戊醇4.3 mL，催化剂1.5 g，反应时间4 h。实验结果见表6。

表6 模型的验证实验数据Table 6 Model validation of experimental data

从表6可以看到实验重现性很好，方法2条件下的工艺稳定性很高，且方法2比方法1得到的最优组合 A-1B1C-1的酯化率高，故最后确定最佳工艺条件为反应时间4 h，催化剂用量1.5 g(水杨酸质量的14.16%)，醇酸摩尔比为4。

3 结 论

将回归分析与最优化方法应用于正交试验，不仅可以根据正交试验结果得到指标与试验参数之间定性的关系，也可以得到两者之间连续的定量关系，使得试验次数减少。本文采用三因素二水平一次回归正交设计方法，以酯化率为指标，建立指标与因素的回归方程（模型）。

确定了最佳反应条件为：反应时间4 h，催化剂用量1.5 g (水杨酸质量的14.16%)、醇酸摩尔比为4；主次影响因素为催化剂用量>催化剂与醇酸摩尔比的交互作用>醇酸摩尔比。这为工业化生产提供了便捷的工艺优化模型。

[1] 杨林.键参数拓扑指数与湘系元素物性的多元分析[J].计算机与应用化学，2002，19(4):4615-463.．

[2] 徐淑红，马春燕，张静文，奚旦立 .正交设计与回归分析在河道底泥陶粒制备中的应用[J]. 中国陶瓷.2008,44(9)：63-65.．

[3] 刘严.多元线性回归的数学模型[J].沈阳工程学院学报（自然科学版），2005，1(2，3)：128-129.

[4] 李军, 黄海宽, 曹琦 .基于支持向量机的中药工艺参数优化研究[J].计算机工程与应用，2007，36(43)：205-207.

[5] 李洪涛, 周文宗, 高红莉, 张硌.运用均匀设计法检验盐度和碱度对泥鳅的联合毒性作用[J].水产科学，2006，25(11)：565-568.

[6] 童金华,林启训 .均匀设计法优化枇杷果核棕色素提取工艺[J].特产研究，2006，(1)：9-13

[7] 晋玉秀,杨秀培,刘建军,蔡铎昌.均匀设计法阴极还原处理含铜废水的研究[J] .河北冶金，2005，(6)：31-33.

[8] 李云雁. 试验设计与数据处理[M].北京：化学工业出版社，2008.

[9] 刘俊先，王汝敏，孙曼灵. 回归正交设计在一增韧酚醛树脂研究中的应用[J].工程塑料应用，2003，31（10）：29-31.

[10] 邓斌,陈六平,俞秋.稀土复合固体超强酸SO42-/ZrO2-Nd2O3催化合成乳酸正丁酯[J].中国调味品，2008，8：48-51.

[11] 徐景士,陈慧宗,彭爱青,黄园英.固体超强酸催化合成水杨酸异戊酯的研究[J] .江西师范大学学报，1998，22(2)：150-152.

[12] 庄楚强，吴亚森.应用数理统计基础[M].广州：华南理工大学出版社，2002.

[13] Micosoft.Micmsoft Excel 5工作表函数手册[M]. 方中,译.北京：清华大学出版社，1995.

Optimization of Synthesis Conditions of Isoamyl Salicylate by Regression Orthogonal Experiment

LIU Zheng，LIU Bao-yu，CHENG Shi-liang，WANG Guo-rui，MO Qiu-sheng
(College of Chemical and Biological Engineering , Guilin University of Technology, Guangxi Guilin 541004, China)

Synthesis conditions of isoamyl salicylate over the solid superacid SO42-/TiO2-Nd2O3catalyst were optimized and modeled by linear regression orthogonal experiment，order of influencing factors was determined. Then regression equation of esterification rate and influence factors was obtained, and the regression equation was verified ,at last it was used to guide to improve the technology. The results show that the regression equation can predict esterification rate of the process system very well, and guide to improve the technology conditions.

Isoamyl salicylate;Solid superacid;Regression orthogonal design;Technology optimization

TQ 651

A

1671-0460（2011）01-0014-04

广西高校优秀人才资助计划项目(NO.RC2007021)、广西研究生科研创新项目、广西研究生教育创新人才联合培养基地项目。

2010-08-20

刘 峥（1962-），女，江西兴国人，教授，博士，研究方向：应用有机合成。E-mail：lisa4.6@163.com，电话：0773-5896859。