基于分数阶傅里叶变换的脉内信号调制方式识别

宁 辉,陈 超

(1.北京航空工程技术研究中心特设研究室,北京100076;2.空军航空大学航空电子工程系,长春130022)

1 引 言

目前,大带宽和复杂波形的雷达信号在军事领域中得到了广泛应用,常规的雷达脉冲描述字已很难准确描述这种雷达信号的特征。为了更加有效地检测雷达信号,对雷达进行脉内特征的识别已经成为一项紧迫而严峻的任务。近年来,在雷达信号脉内调制识别技术的研究领域,出现了许多较为新颖的识别算法和相关技术,主要包括瞬时自相关算法、瞬时频率法、短时傅里叶分析、小波分析等[1-3]。上述这些方法在对线性调频、相位编码等信号进行脉内调制分析时,都取得了一定的效果,但都存在着缺陷[4,5]。

在目前的工程实践当中,最为常用的脉内调制识别方法是瞬时自相关算法。该算法的原理简单,易于工程实现。在简单的信号环境下[6,7],该算法可以比较准确地识别出线性调频信号、频率编码信号和相位编码信号,在信噪比优于10 dB的条件下,3种调制类型的识别率分别可以达到 97%、92%和91%。但是该算法的抗噪性能较差,随着信噪比的降低,识别性能急剧下降;当信噪比降低至0 dB时,会产生严重的误判,对线性调频信号的识别率降为46%,而且无法对其它调制方式进行识别。

基于以上问题,本文通过分析不同调制方式在调频斜率上的区别和特点,提出一种基于分数阶傅里叶变换(Fractional Fourier Transform,FRFT)的脉内信号调制方式的识别算法。该算法可以在低信噪比下完成线性调频信号、频率编码信号和相位编码信号的识别,为日后的工程改进提供了一种新思路。

2 雷达信号的脉内特征

雷达信号的脉内特征可分为人为调制和附带调制,本文研究的对象是人为调制。人为脉内调制包括频率调制和相位编码[2]。

2.1 频率调制信号

为了提高距离分辨能力,常利用各种频率调制方式来增大雷达信号的带宽。频率调制的方式较多,本文主要考虑在雷达信号中经常使用到的线性调频信号和频率编码信号。

线性调频脉冲信号是一种脉内频率调制信号。设初始频率为f0,脉宽为 tp,带宽为B,调频斜率为k,幅度为A,线性调频脉冲信号s(t)可以表示为

线性调频信号的时域波形及其频谱如图1所示。

图1 线性调频信号的时域波形及频谱Fig.1 Time domainwaveform and spectrum of LFM

频率编码信号可以看作是脉内离散频率调制信号,频率编码信号的解析表达式如下:

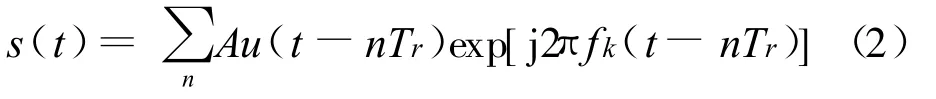
式中,fk为频率码组,子码宽度为 Tr,幅度为 A。图2为频率编码信号的时域波形及其频谱。

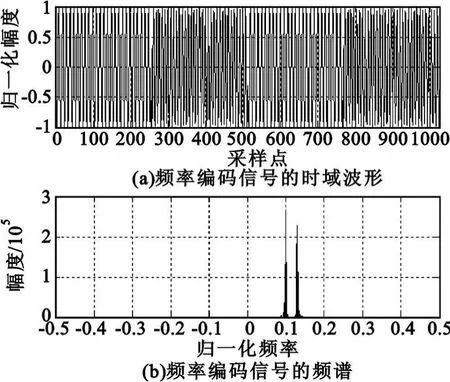
图2 频率编码信号的时域波形及频谱Fig.2 Time domain waveform and spectrum of frequency code signal

2.2 相位编码信号

相位编码信号由许多子脉冲构成,各个子脉冲的宽度相等,相位由一个编码序列决定。如果子脉冲之间的移相值取0和π,即构成二相编码信号;如果子脉冲之间的移相取两个以上的移相值时,则构成多相编码信号。相位编码信号可以表示为

式中,f0为载频,φ(t)为相位调制函数。图3为二相编码信号的时域波形图及其编码序列图,其二进制编码序列为[0101000011011]。

图3 二相编码信号时域波形及其相位编码序列Fig.3 Time domainwaveform and phase-code sequence of two-phase-code signal

3 基于FRFT的脉内调制类型识别

3.1 FRFT的基本原理

设信号为s(t),其FRFT的定义为[8]

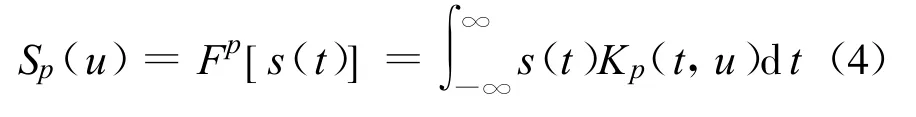
式中,p为 FRFT的阶数,Fp[]为 FRFT的算子,Kp(t,u)为FRFT的变换核,如式(6)所示:

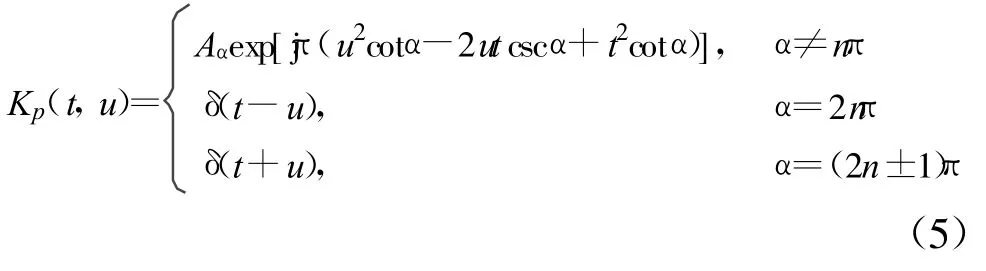
近年来,人们对FRFT的快速数值运算进行了积极的研究,提出了很多FRFT的快速实现算法,其中H.M.Ozaktas[9]提出了分解型快速算法,该算法将FRFT分解为信号的卷积形式,其运算量小,在工程中得到了广泛的应用。将分数阶傅里叶变换的定义重写如下:

由上式可以看出,分解型快速算法将分数阶傅里叶变换分为信号与线性调频函数相乘、进行傅里叶变换、再与线性调频函数相乘、乘以复数因子4个运算。利用以上过程,可以实现对FRFT的快速运算。若用FFT来实现,则在信号长度为N时,计算复杂度仅为O(NlbN),这将大大提高运算速度[10]。

信号s(t)的分数阶傅里叶变换Sp(u)可以看作是s(t)在以逆变核K-p(t,u)为基的函数空间上的展开,而该核是u域上的一组正交的chirp基[11]。线性调频信号在适当的分数阶域中,将表现为一个冲激函数,即分数阶傅里叶变换的某个分数阶域对给定的线性调频信号具有很好的能量聚集特性,因此,FRFT多用于线性调频信号的检测。基于这个特性,本文将从线性调频信号入手,逐步实现脉内调制类型的识别。

3.2 线性调频信号的识别

通过观察图1～3发现:线性调频信号在其脉冲内部频率发生了改变,变化的快慢由调频斜率k决定;而频率编码信号和相位编码信号在其码元内部频率不发生改变,可以认为它们是定频信号,调频斜率k为零。

信号经FRFT后得到的模值为信号的时频分布函数在与时间轴夹角成 α角度的轴线上的投影。若信号的调频斜率与α满足关系k=-cot α,即旋转角度与信号调频斜率匹配时,信号的时频分布在 u轴的投影将出现一个尖峰,当旋转角度与信号的调频斜率不匹配时,信号变换为广义的线性调频信号,投影尖峰将不存在。因此,频率编码信号和相位编码信号经FRFT后,模值会在 α=π/2时(对应分数阶次为1)出现尖峰,而线性调频信号经FRFT后得到的模值尖峰将不会出现在 α=π/2处[12]。

对线性调频信号、频率编码信号以及相位编码信号进行FRFT,取出每个分数阶次中FRFT模最大值,这些最大值随分数阶次p的变化曲线如图4～6所示。

图4 线性调频信号的FR FT模值随分数阶的变化曲线Fig.4 Curve of phase-code signal′s FRFT modular

图5 频率编码信号的FR FT模值随分数阶的变化曲线Fig.5 Curve of phase-code signal′s FRFT modular

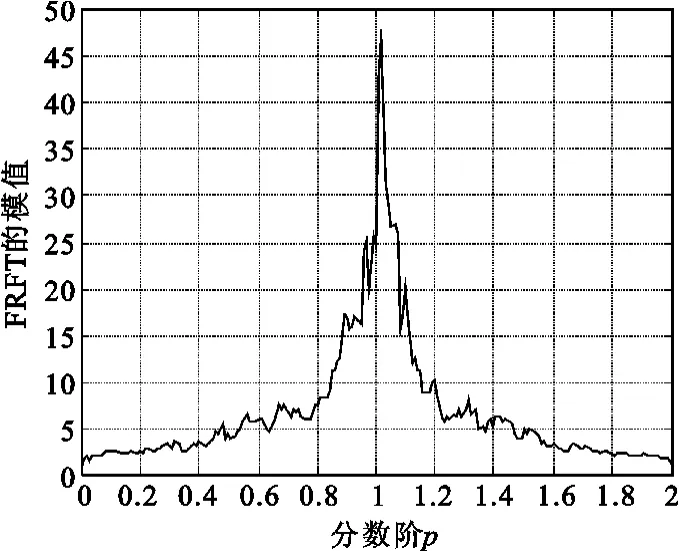
图6 相位编码信号的FRFT模值随分数阶的变化曲线Fig.6 Curve of phase-code signal′s FRFT modular

从图中可以看出,曲线尖峰出现在不同的位置,这些位置反映了信号的调制类型。频率编码信号和相位编码信号的FRFT模最大值在p=1处出现尖峰,且随着p值偏离峰值点,幅度下降相对缓慢。而线性调频信号的FRFT模最大值在与调频斜率匹配的分数阶次处出现尖峰,该峰值仅在对应的p值附近很窄的范围内比较大,偏离峰值点后,幅值急剧下降。

此处,将频率编码信号和相位编码信号统称为编码信号。从图4～6中可以看出,线性调频信号在p=1处的FRFT模最大值非常低,而编码信号的FRFT模最大值在p=1处是明显的尖峰,两者幅度差距明显。因此,依据信号在p=1附近FRFT模最大值的大小,可以实现线性调频信号和编码信号的区分。设信号在p=1附近的FRFT模最大值为S,设定门限St,当S>St时,将信号识别为编码信号;当S≤St时,将信号识别为线性调频信号。

3.3 编码信号的识别

由于频率编码信号和相位编码信号经FRFT得到的模最大值在 p=1处同样存在峰值,因此本文对上述两种信号在分数阶次p=1处进行FRFT。图7和图8为在信噪比为0 dB时,频率编码信号、相位编码信号在 p=1处FRFT的波形图。从图中可以看出,相位编码信号的FRFT仅存在一个峰值,频率编码信号的FRFT存在多个峰值,且峰值个数等于信号分布的频率点数。根据峰值个数的不同,我们可以识别出这两种编码信号。当信号在p=1处的FRFT波形存在有两个以上的峰值时,信号被识别为频率编码信号;当仅存在一个峰值时,信号被识别为相位编码信号。

图7 频率编码信号在 p=1处的FRFT波形Fig.7 Waveform of frequency code signal′s FRFT modular with p=1

图8 相位编码信号在 p=1处的FRFT波形Fig.8 Waveform of phase code signal′s FRFT modular with p=1

4 算法性能分析

为了验证算法的有效性,本文在信噪比为-4～10 dB的条件下,对随机生成的线性调频信号、频率编码信号和相位编码信号进行FRFT,并依据本文设计的方法进行调制方式识别。每个信噪比整数值点进行Monte-Carlo实验500次,绘制识别概率曲线,如图9所示。

图9 识别概率曲线Fig.9 Curve of recognition probability

观察图9中的曲线可以发现,在信噪比降为-2 dB时,FRFT仍可以较好地完成脉内信号调制方式的识别。该条件下,频率编码信号的识别率最高,接近90%;线性调频信号次之,达到了85%;而相位编码信号的识别率最低,为77%。产生错误的原因是由于噪声的影响,随着信噪比的降低,信号在p=1附近的FRFT模值不能正确反映出信号的频率调制特征,造成识别错误。由于相位编码信号在其相位突变处存在频率的变化,在噪声的影响下,信号在p=1处的FRFT波形出现多个峰值,因此被识别为频率编码信号。而频率编码信号可以看作是多个常规信号的组合,因而在识别过程中受噪声影响较小,识别率较高。

将基于FRFT的调制方式识别结果与瞬时自相关算法的识别结果作比较,表1列出了信噪比为0 dB时两种算法的识别结果,从另一个角度验证了本文算法的有效性。通过本文的识别方法,可以大幅度提高低信噪比下线性调频信号的识别概率(在0 dB时,从46%提高到了88%),并完成了低信噪比下频率编码信号和相位编码信号的识别。

表1 信噪比为0 dB时脉内信号调制方式的识别概率Table 1 Recognition probability of radar intra-pulse signals modulation when SNR=0 dB

综上,本文设计的基于FRFT的脉内信号调制方式识别方法能够完成对3种常用脉内调制方式的识别,在信噪比优于-2 dB的条件下,达到了较好的识别效果,具有一定的抗噪性能。识别过程中,所采用的FRFT仅是在分数阶数p=1上进行的,省去了对所有分数阶域的搜索,节省了识别时间和存储空间,提高了效率。

5 结束语

雷达信号的脉内调制方式识别是参数估计的前期工作,其意义重大。现代雷达信号的脉内调制方式趋于复杂化、多样化,本文所针对的3种调制方式属于初级的脉内调制方式特征,它们还可以进一步划分为二相编码信号、四相编码信号、V型调频信号等细微的脉内调制方式[1]。从这个角度来讲,本文设计的识别方法是一种初级的识别模型,在此基础上如何进一步识别脉内信号的细微特征,构建一个完整的脉内调制特征识别系统,将是本文后续工作的研究重点。

[1]Mark A Richards.雷达信号处理基础[M].北京:电子工业出版社,2008.Mark A Richards.Fundamentals of Radar Signal Processing[M].Beijing:Publishing House of ElectronicsIndustry,2008.(in Chinese)

[2]Richard G Wiley.ELINT:The Interception and Analysis of Radar Signals[M].Norwood,MA:Anech House,2006.

[3]Kawalec A,Owczarek R.Radar emitter recognition using intrapulse data[C]//Proceedings of the 15th International Conference on Microwaves,Radar andWireless Communications.Warsaw,Poland:IEEE,2000:435-438.

[4]姜勤波,马红光,杨利锋.一种新的雷达脉冲信号的非匹配检测算法[J].现代雷达,2006,28(11):36-40.JIANG Qin-bo,MA Hong-guang,YANG Li-feng.A Novel Nonmatched DetectionAlgorithm of Radar Pulse Signal[J].Modem Radar,2006,28(11):36-40.(in Chinese)

[5]李振兴,张国毅.基于调制域的雷达信号脉内特征提取新方法[J].电讯技术,2010,50(12):69-74.LI Zhen-xing,ZHANG Guo-yi.A New Intra-pulse Feature Extraction Approach for Radar Signals Based onModulation Domain[J].Telecommunication Engineering,2010,50(12):69-74.(in Chinese)

[6]邹顺.雷达信号分选与细微特征分析[D].西安:西北工业大学,2006:46-50.ZOU Shun.Analysis of Fine—feature for Radar Signal[D].Xi′an:Northwestern Polytechnical University,2006:46-50.(in Chinese)

[7]ZHANG Ge-xiang,HU Lai-zhao,JIN Wei-dong.Resemblance coefficient based intra pulse feature extraction approach for radar emitter signals[J].Chinese Journal of Electronics,2005,14(2):337-341.

[8]唐向宏,李齐良.时频分析与小波变换[M].北京:科学出版社,2008.TANG Xiang-hong,LI Qi-liang.Time-frequency Analysis and Wavelet Transform[M].Beijing:Science Press,2008.(in Chinese)

[9]HaldunM Ozatkas,OrhanArikan,Alper M Kutay.Digital Computation of the Fractional Fourier Transform[J].IEEE Transactions on Signal Processing,1996,44(9):2141-2150.

[10]赵兴浩,陶然,邓兵,等.分数阶傅里叶变换的快速计算新方法[J].电子学报,2007,35(6):1089-1093.ZHAO Xing-hao,T AO Ran,DENG Bing,et al.Ne w Methods for Fast Computation of Fractional Fourier Transform[J].Acta Electronica Sinica,2007,35(6):1089-1093.(inChinese)

[11]LIU Feng,HUANG Yu,TAO Ran,et al.Chirp-Rate Resolution of Fractional Fourier Transform inMulti-component LFM Signal[J].Journal of Beijing Institute of Technology,2009,8(1):74-78.

[12]QI Lin,TAO Ran,ZHOU Si-yong.Rejectionof Linear FM Interference in DSSS System Based on Fractional Fourier Transform[J].Journal of Beijing Institute of Technology,2005,14(2):158-161.