基于TDC的GPS驯服恒温晶振系统设计

陆加海,张同双,陶小红,陈浩谦,李春海

(1.上海交通大学,上海200030;2.中国卫星海上测控部,江苏江阴 214431)

1 引 言

测控系统要求有高精度的时间频率系统。为了保持站点间时间同步,一般采用铷原子钟或恒温晶振(Oven-Controlled Crystal Oscillator,OCXO)来提供时间频率信号。前者的成本较高,后者频率准确度较差,不能满足测控系统的指标要求。

为解决上述问题,本文采用GPS对恒温晶振进行驯服,综合了GPS时间信号长稳指标高的优点和恒温晶振短稳指标高的优点,从而获得了高稳定度和高准确度的频率信号。

为了计算恒温晶振相对于GPS的频率偏差,需要长时间测量GPS秒信号与恒温晶振分频信号之间的时差,通过时差计算得到频率偏差,再根据频率偏差来校准恒温晶振,所以时差测量的精度直接影响到频率驯服的精度。文献[1]采用FGPA延迟线内插法测时差,测量精度达到121 ps,但测量线性化较差、成本高。文献[2]介绍了模拟内插法测时差,测量精度达到400 ps,但易受噪声干扰、实现困难;

本文采用时间数字转换器(Time to Digital Converter,TDC)测量时差,精度达到250 ps,极大减小了测量误差,且设计简单、成本低,有效实现了GPS驯服恒温晶振系统的设计。

2 系统设计

2.1 系统硬件组成

系统组成框图如图1所示,主要由GPS模块、TDC时间数字转换器、分频模块、数据处理单元、D/A转换模块和恒温晶振等组成。GPS模块用于输出标准的GPS秒脉冲信号,分频模块将恒温晶振频率信号分频成1 PPS信号送TDC模块,TDC模块用于测量恒温晶振分频1 PPS信号与GPS秒信号之间的时差,数据处理单元对时差数据进行处理后得到恒温晶振相对于GPS的频率偏差,并控制D/A转换模块对恒温晶振进行频率修正。

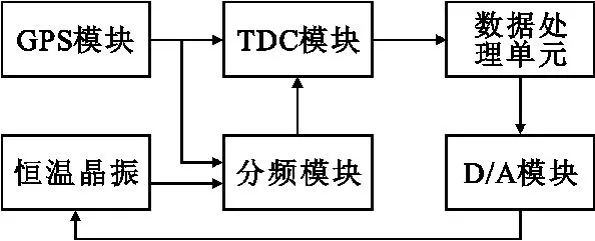
图1 系统组成框图Fig.1 Block diagram of the system

2.2 时差测量电路设计

TDC是时间数字转换器的英文缩写。这类芯片把时差直接转化为高精度的数字值。它们被描述为与ADC(模拟数字转换器)功能相似的器件。通常TDC是用在分辨率小于1 ns的测量场合。本设计使用TDC-GP1芯片进行测量,其测量电路框图如图2所示。将待测的GPS秒信号和晶振1 PPS信号送TDC模块;START信号由分频模块产生并送TDC模块,用于控制测量时序。TDC模块将时差转化为数字值送数据处理单元。

图2 时差测量电路框图Fig.2 Block diagram of time difference measurement circuit

时差在TDC模块的测量时序如图 3所示,将GPS秒信号与恒温晶振分频得到的1 PPS信号进行比对,得到的时间间隔即是待测的时差。

图3 时差测量时序图Fig.3 Time difference measurement timing diagram

图3中START信号为测试开始信号,GPS秒信号与晶振1 PPS信号之间的时间间隔T为待测的时差。信号脉冲宽度要求大于2.5 ns,开始信号与被测信号之间时间间隔要求大于3 ns、小于7.6 μ s。

为了保证每次被测信号落在允许的测量范围内。测量开始之前应进行初步的时间同步,确保GPS秒与晶振1 PPS之间的时差小于3 μ s。START信号通过将GPS秒延时约999 996 μ s后产生,确保START信号与GPS秒信号之间的时差保持在4 μ s左右。

2.3 分频模块的设计

分频模块采用CPLD设计实现,通过CPLD分频计数将恒温晶振的10 MHz频率信号分频为1 PPS信号,同时将 GPS秒延时999 996 μ s后生成 START信号,确保START信号超前GPS秒信号4 μ s。当晶振1 PPS与GPS秒之间的时差大于3 μ s时通过计数器清零的方法进行同步,确保两者之间的时差小于3 μ s。其时序如图4所示。

图4 分频模块时序图Fig.4 Timing diagram of frequency division module

3 数据处理

根据频率和周期互为倒数的关系,可采用测时差的方法[4](以GPS的秒信号为参考)来测量本地频率源的频率准确度(Δf/f),作为校频的依据。计算公式如下:

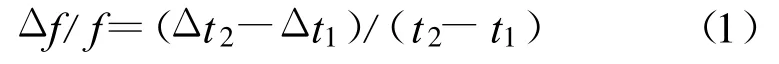
按照公式(1)可以计算出恒温晶振相对于GPS的频率偏差[5],其中 Δt2、Δt1分别为 t2、t1时刻测得的晶振1 PPS与GPS秒之间的时差值。根据频率偏差的大小,将需要调整的频率偏差量转换为模拟电压施加在压控恒温晶振的电压控制端,便可以实现对恒温晶振进行频率修正。

但GPS信号在传输过程中存在各种干扰[3],这些干扰造成GPS输出的秒信号存在一定的抖动,其短稳较差。通过对时差值进行递推平均滤波可以有效消除GPS秒信号抖动的影响[6]。取测量得到的时差数据 Δt1,Δt2,Δt3,…,Δtn,…,以 n 作为窗口长度对其中的n个测量值取平均,通过移动窗口得到新的时差数据序列[1]ΔT1,ΔT2,ΔT3,…,ΔTn,…,如公式(2)所示:

为了使频率准确度 Δf/f测量更准确,对递推平均滤波算法进行优化,取 ΔTj,ΔTn+j,ΔT2n+j,ΔT3n+j,…,ΔTmn+j,…,作为实际测量序列进行计算,如公式(3)所示:

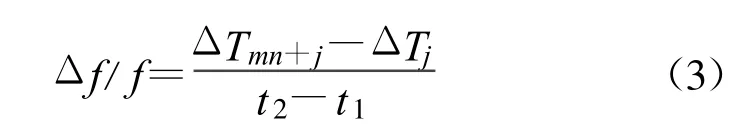
将式(2)代入式(3)得到

图5是使用本系统测量得到的恒温晶振相对于GPS系统的时差曲线,该曲线由于GPS秒信号抖动而存在一定的波动,使用这些数据计算得到的频率偏差也会受到影响而发生波动,所以不能直接使用。图6是添加递推平均滤波处理后得到的时差数据,其滤波窗口n设置为120。滤波后时差数据的抖动减小约两个数量级。

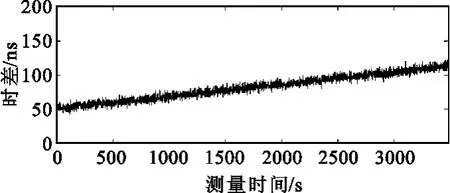
图5 时差数据滤波前曲线Fig.5 Curve before time difference data filtering

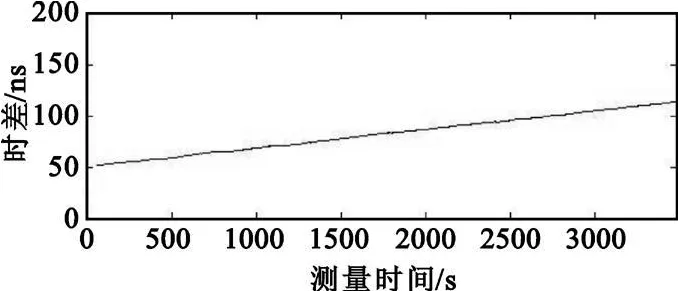
图6 时差数据滤波后曲线Fig.6 Curve after time difference data filtering

频率调节通过16位DAC(数字模拟转换器)实现,将需要调整的频率偏差值转换为模拟电压,施加在恒温晶振的控制电压输入端,实现对恒温晶振频率的调控。

4 试 验

本设计中采用MV180 OCXO双层恒温晶振,其频率牵引范围为±3×10-7,外部控制电压范围为0～+5 V。GPS模块采用Motolora M12+,在位置保持模式下,输出秒信号的抖动方差 σ<20 ns。时间数字转换器使用TDC-GP1芯片,其测量精度达到250 ps,测量误差远小于GPS秒信号抖动引入的误差。16位数模转换芯片采用DAC8571,其输出电压对恒温晶振的理论频率调谐灵敏度优于1×10-11。图7所示为根据滤波后的时差数据计算得到的频率准确度曲线。不采用滤波算法频率驯服时间为数个小时,采用滤波算法后频率驯服时间缩短为约1 200 s。实验表明,驯服后恒温晶振的频率准确度优于3×10-11。

图7 驯服后频率准确度曲线Fig.7 Tamed frequency accuracy curve

5 小 结

本文通过采用时间数字转换器测量时差,简化了GPS驯服恒温晶振系统的硬件设计,测量精度达到250 ps,极大减小了测量误差。设计了优化的递推平均滤波算法对时差数据进行滤波处理,消除了GPS秒信号抖动引入的干扰,缩短了频率驯服时间。频率驯服时间约为1 200 s,与国内同类应用相比,缩短约一个数量级;频率驯服精度优于3×10-11。

[1]卢祥弘,陈儒军,何展翔.基于FPGA的恒温晶振频率校准系统的设计[J].电子技术应用,2010(7):104-107.LU Xiang-hong,CHEN Ru-jun,HE Zhan-xiang.The designof frequency calibrationsystem for OCXO based onFPGA[J].Measurement Control Technology and Instruments,2010(7):104-107.(in Chinese)

[2]孙杰,潘继飞.高精度时间间隔测量方法综述[J].计算机测量与控制,2007,15(2):145-148.SUN Jie,PAN Ji-fei.Methods of High Precision Time-Interval Measurement[J].Computer Measurement&Control,2007,15(2):145-148.(in Chinese)

[3]单庆晓,杨俊.卫星驯服时钟系统的新进展[J].测试技术学报,2009,23(5):396-401.SHAN Qing-xiao,YANG Jun.Review of Satellite Disciplined Clock System[J].Journal of Test and Measurement Technology,2009,23(5):396-401.(in Chinese)

[4]杨旭海,翟惠生,胡永辉,等.基于新校频算法的GPS可驯铷钟系统研究[J].仪器仪表学报,2005,26(1):41-44.YANG Xu-hai,ZHAI Hui-sheng,HU Yong-hui,et al.Study on GPS Disciplined Rb Clock Based on New Frequency Accuracy Measurement Algorithm[J].Chinese Journal of Scientific Instrument,2005,26(1):41-44.(in Chinese)

[5]ValdesM D,Villares IFarina J,Moure M J.A FPGA-based frequency measurement system for high—accuracy QCM sensors[J].Industrial Electronics,2008,34(11):1707-1712.

[6]Cadenas O,Megson G.Pipelining considerations for an FPGA case[C]//Proceedings of 2001IEEE International Symposium on Digital Systems Design.Warsaw,Poland:IEEE,2001:276-283.