基于物理层网络编码的非对称中继系统性能分析
2011-09-28王江洪
王江洪,谢 红
(哈尔滨工程大学信息与通信工程学院,哈尔滨150001)
1 引 言
网络编码(Network Coding,NC)由香港中文大学的R.Ahlswede、N.Cai、S.-Y.R.Li以及 R.W.Yeung于2000年首次提出[1],因其广播特性适于应用在无线网络中进行信息传输,从而吸引了众多学者进行相关研究,并有了大量的研究成果。典型的网络编码对已知信息采用简单的“异或”操作进行处理。网络编码的优势在于可以使网络以理论上界容量(根据最大流-最小割原理确定)进行数据传输。
N.Cai等在文献[2]中提出了线性网络编码的概念,详细论述了线性范围内达到系统理论容量界的问题,即仅在节点处进行线性网络编码,就可以达到网络的理论上限。Wu Y等在文献[3]中研究了双向中继网络中基于XOR运算的信息交换方法。
物理层网络编码(Physical-layer Network Coding,PNC)[4-6]通过在节点处采用恰当的调制解调技术,使得无线电磁波信号的叠加与数据比特流间建立起映射关系,将由于无线链路广播特性引起的信号间干扰转换为网络编码操作的一部分,从而改善系统性能并有效提升系统的吞吐量。
Louie等在文献[7]中详细论述了物理层网络编码在双向中继网络中的性能,从传输速率和误比特率方面进行了比较和分析。
分层调制(Hierarchical Modulation,HM)[8-10]技术将广播通信信号分为两种不同类型,根据数据不同的优先级给予不同的保护,即将高优先级的数据调制到高保护的比特位,低优先级的数据调制到低保护的比特位。该技术已经应用于数字广播通信系统DVB-T标准中。
在现有基于网络编码的中继网络研究中,均假设网络是对称的,而对于中继位置不对称造成的系统性能下降关注较少。本文针对这一情况,提出了基于物理层网络编码的分层调制(HMPNC)技术,分别在加性高斯白噪声信道和瑞利信道条件下进行了性能仿真,并给出了仿真结果和分析。
2 网络编码在中继网络的应用
本文研究基于三节点中继网络,该网络包括一个源节点S、一个中继节点R和一个目的节点D。源节点和目的节点通过中继节点进行信息交换。
在三节点中继网络中,源节点和目的节点需要经过4个时隙才能完成信息交换。而采用物理层网络编码后,只需要两个时隙就可以完成,如图1所示。
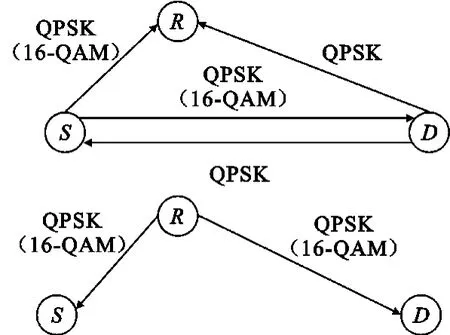
图1 基于PNC的非对称三节点中继网络Fig.1 Three-node asymmetric relay network based on PNC
第一时隙:源节点和目的节点同时向中继节点和对方发送数据;
第二时隙:中继节点将第一时隙接收到的数据进行物理层网络编码后,广播给源节点和目的节点。源节点和目的节点接收到中继节点广播的数据后,经过相应处理,就可以得到所需的信息。
假设S-R间信道条件优于D-R间信道条件,且任意两节点间的信道条件是相互的,即S-R与R-S链路拥有相同的信道条件。
本文共考虑3种方案进行性能比较。
方案一:各节点均采用QPSK调制,称作常规调制(Conventional Modulation,CM)方案;
方案二:源节点S采用16-QAM调制,中继节点R和目的节点D采用QPSK调制,称作非对称调制(Asymmetric Modulation,AM)方案;
方案三:源节点S采用分层调制4/16-QAM,中继节点R和目的节点D仍采用QPSK调制,称作物理层网络编码分层调制(HMPNC)方案。
HMPNC方案如图2所示,源节点S采用4/16-QAM分层调制方法,将数据分成高优先级SH和低优先级SL两部分进行传输。中继节点R和目的节点D仍采用QPSK调制。

图2 HMPNC方案Fig.2 HMPNC scheme
图3显示了源节点S采用4/16-QAM调制时的星座图,定义d、d1和d2:2d1表示黑色QPSK星座点间距离;2d2表示一个象限内灰色QPSK星座点间的距离;2d表示相邻象限间灰色QPSK星座点间的距离。定义星座优先级参数以此来判定两个数据流的优先级。当0<λ<1时,SH数据具有高优先级,反之当λ>1时,SH数据具有低优先级。

图3 4/16-QAM调制Fig.3 4/16-QAM modulation
3 误比特率和系统容量分析
定义 γi,j表示i与j间链路的平均信噪比,例如R表示源节点S和中继节点R间平均信噪比,且
3.1 CM方案端对端误比特率分析
源节点S和目的节点D的误比特率(BER)[11]:

式中,i∈(S,D)。
同理,中继节点R的误比特率:

假设SR和RD链路无误时,来自DR链路的错误比特信息在中继节点处经过网络编码操作,生成新的比特信息进行广播后,将导致最终的译码错误。同理,任意两条链路同时出错,则不会影响最终的译码结果。根据以上原理,可以得到公式:

源节点S的端对端误比特率可表示为
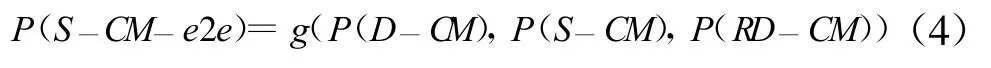
目的节点D的端对端误比特率可表示为
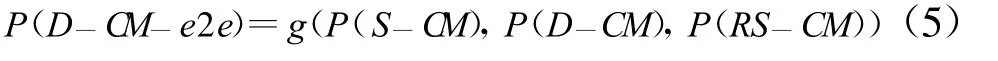
3.2 AM方案端对端误比特率分析
在AM方案中,源节点S和中继节点采用16-QAM调制,目的节点D采用QPSK调制。
当中继节点在第二时隙进行网络编码操作时,需要将目的节点发送的数据进行加冗余处理(如加零等操作),并在RD链路传输经16-QAM调制的数据(即S D′)。由于RD 链路信道条件较差,仅能保证QPSK信号的传输,而高阶调制信号(16-QAM)将会遭受严重的衰落影响,进而引起整个系统性能的下降,具体性能曲线将在仿真结果中给出。
3.3 HMPNC方案端对端误比特率分析
由文献[12]可知,当源节点 S采用分层调制时,高优先级数据流SH和低优先级数据流SL的误比特率分别为

其中:

式中,λ和M分别表示星座优先级参数及调制级数。
同样,可以得到目的节点D和中继节点R处的误比特率公式:
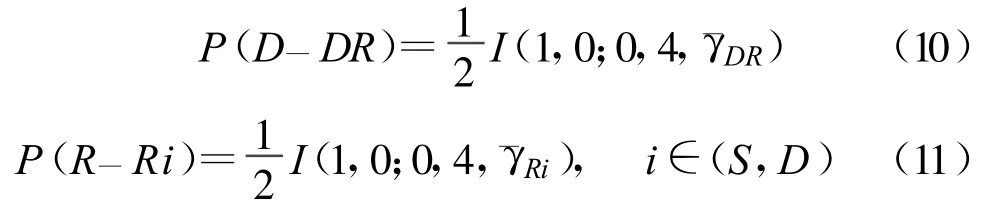
根据公式(6)~(11)可以得到系统端对端误比特率:

3.4 系统遍历容量分析
设源节点S生成信号形式为

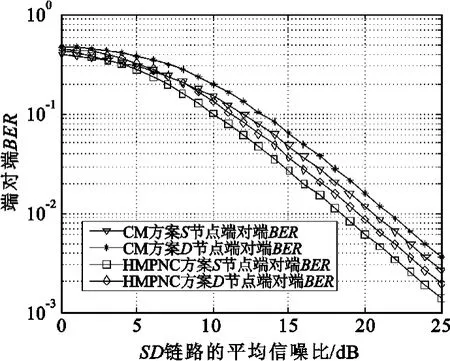
其中,0 其中,信道参数 hSR和hSD间相互独立同分布,噪声nj为零均值、方差为 Ψ的复高斯随机变量。可得到第一时隙中继节点和目的节点接收数据SH和SL时的瞬时信噪比为 同理,第二时隙,源节点和目的节点接收到中继节点广播的、经网络编码操作后的数据时的瞬时信噪比为 由于数据SH可理解为通过直接链路(SD链路)进行传输,则其传输速率仅与SD链路的信道状态有关。而数据SL需经过SR链路和RD链路,其传输速率取决于两条链路的信道状态。利用香农公式: 可以推出数据SH和SL的最大传输速率为 其中,E[·]表示求统计平均,ti表示单位时隙所需时间。 为了能显著展现中继节点位置对系统遍历容量的影响,引入路径距离参数δ和路径损耗参数β,则可得各链路平均信噪比与两参数间关系: 直接传输方案(Direct Transmission,DT)的系统遍历容量公式如下: 首先比较各方案的端对端误比特率,假设 γDR 通过图4、图5和图6的性能曲线对比可以看出,HMPNC方案的抗噪性能要优于CM方案和AM方案。 图4是在AWGN信道下CM方案与HMPNC方案性能仿真。仿真结果显示,在AWGN信道高信噪比条件下,源节点S处的端对端误比特率为10-4时有大约1.5 dB的性能增益。 图4 AWGN信道下CM方案与HMPNC方案性能对比Fig.4 Performance comparison between CM scheme and HMPNC scheme under AWGN channel 图5是在AWGN信道下AM方案与HMPNC方案端对端误比特率性能仿真。仿真结果显示,在AWGN信道高信噪比条件下,源节点S与目的节点D的端对端误比特率性能均得到一定提升。 图5 AWGN信道下AM方案与HMPNC方案端对端误比特率性能Fig.5 End-to-end BER performance of AM scheme and HMPNC scheme under AWGN channel 图6和图7分别是在Rayleigh信道下CM方案与HMPNC方案、AM方案与HMPNC方案端对端误比特率性能。仿真结果显示,虽然HMPNC方案抗噪性能仍为最优,但是系统性能较AWGN信道条件时有大幅下降,说明在较差信道条件下,如要获得更好的抗噪性能,仅靠改变调制方法不足以达到目的,需要与其它技术相结合,这也是下一步的研究方向。 图6 Rayleigh信道下CM方案与HMPNC方案端对端误比特率性能Fig.6 End-to-end BER performance of CM scheme and HMPNC scheme under Rayleigh channel 图7 Rayleigh信道下AM方案与HMPNC方案端对端误比特率性能Fig.7 End-to-end BER performance of AM scheme and HMPNC scheme under Rayleigh channel 同时,为了讨论不同的 λ值对系统性能的影响,采用不同的 λ值对系统进行仿真。图8显示了在AWGN信道条件下,HMPNC方案采用不同 λ值对系统性能的影响。 图8 AWGN信道下HMPNC方案不同 λ值性能对比Fig.8 Performance comparison of HMPNC scheme with different λunder Rayleigh channel 可以看出,随着 λ值的增大,源节点S的性能逐渐下降,这与λ值的定义是相符合的。λ值变化导致分层调制的星座点间距离变化,影响了数据流的优先级,因此,根据系统需求合理设置星座图,可以得到满意的系统性能。 假设链路SD间的平均信噪比为 γSD=5 dB,路径损耗参数β=4。 由图9可以看出,当中继节点到源节点和目的节点距离相等时,系统遍历容量达到峰值。 图9 系统遍历容量对比Fig.9 Ergodic capacity comparison of four schemes HMPNC方案由于采用了物理层网络编码,减少了传输时隙,较传统双向中继方案(四时隙传输)和传统网络编码方案(三时隙传输)分别提高了50%和33%的系统容量。 本文提出了一种应用于非对称双向中继网络的基于物理层网络编码的分层调制方案,进行了端对端误比特率和系统遍历容量的性能仿真及分析。仿真结果显示提出的方案可以有效提高系统的抗噪性能,并且较以往的中继传输方案较大幅度提升了系统遍历容量。同时,对 λ值的仿真显示,根据不同的通信要求,改变星座点间距离,以此影响数据流的优先级,改变系统的性能。 但该方案在信道条件较差时(如Rayleigh信道)抗噪性能有一定的下降,下一步将研究该方案与其它抗噪技术结合的方案,来进一步提升系统的抗噪能力。 [1]Ahlswede R,Cai N,Li S Y R,et al.Network information flow[J].IEEE Transactions on Information Theory,2000,46(4):1204-1216. [2]Li S Y R,Yeung R W,Cai N.Linear NetworkCoding[J].IEEE Transactions on Information Theory,2003,49(2):371-381. [3]Wu Y,Chou P A,Kung S Y.Information exchange inwireless networks with network coding and physical-layer broadcast[C]//Proceedings of the 2005 Conference on Information Sciences and Systems.Baltimore,MD,USA:IEEE,2005:1-4. [4]Zhang S,Liew S-C,Lam P.Physical-layer network coding[C]//Proceedings of the 12th Annual International Conference on Mobile Computing and Networking.Los Angeles,CA,USA:IEEE,2006:358-365. [5]Zhang S,Liew S-C,Lam P.On the Synchronization of Physical-layer Network Coding[C]//Proceedings of the 2006 IEEE Information Theory Workshop.Chengdu:IEEE,2006:404-408. [6]Chen Y D,Kishore S,Li J T.Wireless Diversity through Network Coding[C]//Proceedigns of Wireless Communications and Networking Conference.San Francisco,CA:IEEE,2006:1681-1686. [7]Louie RH Y,Yonghui Li,Vucetic B.Practical physical layer network coding for two-way relay channels:performance analysis and comparison[J].IEEE Transactions on Wireless Communications,2010,19(2):764-777. [8]Jiang H,Wilford P A.A hierarchical modulation for upgrading digital broadcast systems[J].IEEE Transactions on Broadcasting,2005,51(2):223-229. [9]HauslC,Hagenauer J.Relay communicationwith hierarchical modulation[J].IEEE Communication Letters,2007,11(1):64-66. [10]Jung Min Park,Seong-Lyun Kim,Jinho Choi.Hierarchically Modulated Network Coding for Asymmetric Two-Way Relay Systems[J].IEEE Transactions on Vehicular Technology,2010,59(5):2179-2184. [11]Proakis J G.Digital Communications[M].5th ed.Singapore:McGraw-Hill Book Co.,2007. [12]Vitthaladevuni P K,Alouini M-S.BER computation of 4/M-QAM hierarchical constellations[J].IEEE Transactions on Broadcast,2001,47(3):228-238.



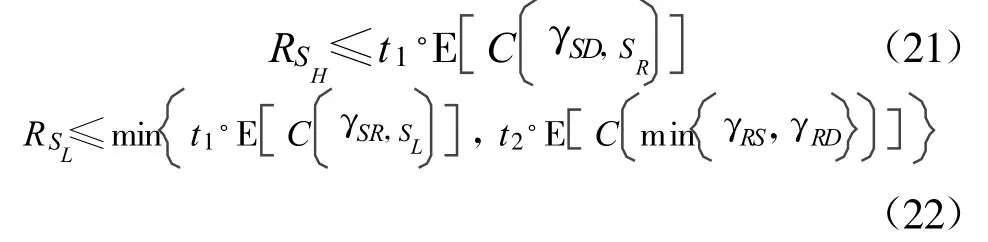
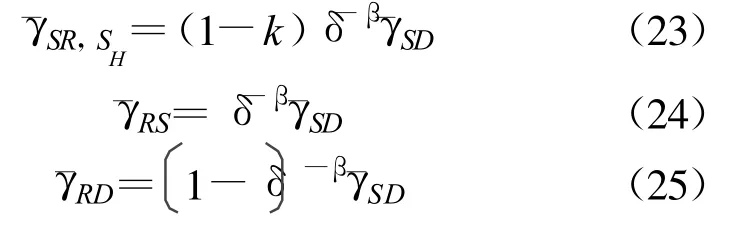

4 系统仿真及结果分析
4.1 端对端误比特率性能仿真结果





4.2 系统遍历容量仿真结果

5 结 论
