功率因数校正Boost变换器中快时标不稳定的形成与参数动态共振*

程为彬 康思民 汪跃龙 汤 楠 郭颖娜 霍爱清

(西安石油大学电子工程学院，西安 710065)

功率因数校正Boost变换器中快时标不稳定的形成与参数动态共振*

程为彬康思民 汪跃龙 汤 楠 郭颖娜 霍爱清

(西安石油大学电子工程学院，西安 710065)

(2010年5月5日收到;2010年6月3日收到修改稿)

以动态调整过程中的动态特征系数积和动态镇定能力为基础，研究连续峰值电流模式功率因数校正(PFC) Boost变换器中的快时标不稳定及其不对称混沌现象的形成机理.基于提高功率因数和降低谐波失真的要求，提出输入电流正弦化的补偿思路，应用参数共振优化补偿策略，推导优化补偿的表达式，采用最强参数共振进行全局优化.数值仿真表明这种全局优化补偿策略具有最强的动态镇定能力，保证每个频闪周期内的快速稳定，控制了快时标不稳定混沌现象，获得理想的补偿效果和单位功率因数，可提高变换器的转换效率.

Boost变换器，功率因数校正，快时标不稳定，参数共振

PACS:05.45.-a，05.45.Gg，05.45.Pq

1.引 言

功率因数校正(PFC)Boost(power factor correction boost)变换器的输入电压正弦变化，其中的非线性混沌现象比直流-直流(DC-DC)Boost变换器要复杂得多，采用频闪映射法对峰值电流型 PFC Boost变换器进行研究时，出现了快时标不稳定(fast-scale instability)现象［1—11］.由于大部分研究是在 DC-DC Boost变换器的研究成果基础上开展的，主要集中在对其中混沌分岔现象的分析，对其产生原因尚未能做出合理的解释，同时一些概念和研究思路也需要完善:如采用了DC-DC Boost变换器中的静态分析法，忽略了动态调整过程，采用了不严格的稳定性判据，无法合理地解释快时标不稳定及其不对称现象的形成机理;沿用了DC-DC Boost变换器的研究思路和研究方法，都是对给定的控制方案进行参数优化，无法达到每个工频周期内的全局优化目标，总电流谐波失真大;采用参数微扰来进行混沌控制，镇定能力不足和调整过程较长，无法保证 PFC Boost变换器快速稳定，难以获得全工频周期内的最佳稳定性，这些都制约了对 PFC Boost变换器中混沌行为的正确认识和稳定性控制策略的深入研究.

本文以峰值电流型 PFC Boost变换器为基础，从电路的动态调整过程分析入手，在前人研究的基础上拓展一些概念的定义，讨论快时标混沌不稳定及其不对称现象的产生机理.以高功率因数和低总谐波失真度为优化目标，基于动态镇定能力控制需求，采用逆向思维，提出一种全局优化补偿的思路、策略和技术方法，并进行数值研究，为PFC Boost变换器的稳定性控制以及集成控制芯片的设计提供基础依据.

2.快时标不稳定的形成机理

2.1.电路模型

为对比研究，采用文献［8］中的连续峰值电流控制模式PFC Boost变换器，基本电路如图1(a)所示.由于负载电压端接入较大容量的电解电容，输出电压的纹波与其幅值相比可以忽略，认为输出电压恒定为Vo，电路简化为一阶系统，可得到每个频闪周期内相应的一阶微分方程

其中iL为电感电流，Vi(t)为输入交流电压瞬时值，Vi为输入交流电压有效值，To为工频周期，T为频闪采样周期，Dn为第 n个频闪周期内的控制占空比，Dn∈［0，1］.

图1 PFC Boost变换器的连续峰值电流工作模式 (a)原理电路，(b)无共振时的电流调整过程，(c)斜坡共振的电流调整过程

与以往的研究不同，本文从电路的接通时刻开始研究;实际电路或电路仿真中，变换器需要经历起动和调整过程，再到达稳定或不稳定状态.从图1(a)电路可知:起动开始开关接通，电感充电，电感电流上升，一段时间内电感电流一直小于参考电流，触发器的输出保持为高，Dn为1.充电过程完成后，变换器电路进入调整过程，无参数共振补偿时，PFC Boost变换器的电感电流调整过程如图1(b)所示.

定义in为未采用参数共振时调整过程中频闪周期内电感电流的初值，即第n次频闪采样时刻的电感电流值;Iref(t)为电感参考电流时域曲线;irn为未采用参数斜坡共振时第n个频闪周期内的电感参考电流曲线与电感电流曲线的交点，此时电路中的触发器复位，也称为复位时刻的电感电流值;根据工作原理可得调整过程中PFC Boost变换器的电路离散方程

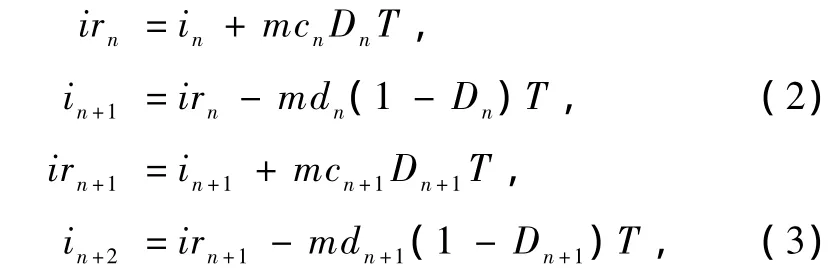
2.2.动态特征系数和可稳定性

相邻频闪周期内的mcn和mdn的取值各自非常接近，简化讨论时认为各自相等，则整理得

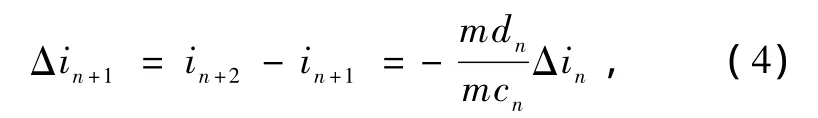
可知相邻的频闪采样时刻的电感电流差值以系数-mdn/mcn变化，定义该系数为PFC Boost变换器的动态特征系数λn，它反映了电路调整过程中的动态镇定能力.当通过控制或者依靠自身能力达到稳定时，λn就成为稳态特征系数 λ，那么在动态调整过程中存在关系式

在通过外界控制或依靠自身能力可以达到稳定的电路(简称可稳定电路)调整过程的各开关周期内取样时刻，电感电流是逐步稳定的，则 Δin+k应趋近于零，即保证 PFC Boost变换器不进入混沌和分岔状态的可稳定条件为-1<λn<1.当输入电压为直流时，即在DC-DC Boost变换器中，其定义也是表示调整过程中的动态镇定能力;当到达稳态时，才存在稳态特征系数λs=Ds/(1-Ds)，表示对参数扰动所产生的混沌现象的固定镇定能力，这在诸多文献中已有较多研究，不再赘述.

动态镇定能力只是表示电路在每个开关周期内具有一定的稳定控制能力，当输入电压保持不变时可以经过一定的调整时间使得电路稳定，并不能说明在后续有限的调整时间中一定能使 PFC Boost变换器稳定下来.

2.3.快时标不稳定的形成过程

输入电压正弦变化的PFC Boost变换器会跨越稳定工作区和不稳定工作区，其动态调整过程中的镇定能力也是动态变化的，而镇定能力决定了PFC Boost变换器是否可以在调整过程中达到稳定以及到达稳定状态的时间长短［12］.以下结合调整过程及其镇定能力，通过仿真来分析 PFC Boost变换器中快时标不稳定及其不对称现象的产生机理，研究采用文献［8］的电路参数:Vi=100 V，Vo=220 V，R= 120 Ω，T=20 μs，L=2 mH，仿真曲线如图2所示.

可以看出，PFC Boost变换器出现快时标不稳定现象与众多文献研究结果是相同的，在输入电压上升段和下降段均出现了快时标不稳定现象，且左右不对称，首先将输入电压上升段的频闪采样电流和控制占空比曲线放大，如图3所示.

图2 PFC Boost变换器的快时标不稳定现象 (a)电感电流和参考电流时域曲线，(b)频闪采样的占空比，(c)频闪采样的电感电流

图3 输入电压上升段的快时标不稳定现象 (a)控制占空比，(b)频闪采样的电感电流值

为定量分析动态调整能力，定义动态特征系数积为一段时间内各开关周期的动态特征系数的乘积若调整过程结束电路达到稳态，则称为可稳定的动态特征系数积;若调整过程结束电路失去稳定，则称为失稳的动态特征系数积.对于PFC Boost变换器的输入电压上升段，可定义从理论上的二分岔开始处(=0.5Vo)到调整过程结束处的动态特征系数积为可稳定的动态特征系数积;由于可稳定电路的动态特征系数是逐步正负振荡衰减的，最后可为零;可令该系数积的绝对值小于某一个数值ε为电路进入稳态的判定依据.在DC-DC Boost电路中，可令ε=0.由于PFC Boost变换器的输入电压一直变化，即使可稳定的动态特征系数积很小，下一个频闪周期内的稳定也是一个输入电压相对扰动的调整过程，即取ε=0是不切实际的.如令ε=0.01，则需要经历31个频闪周期就可以达到基本稳定状态，此时

将输入电压下降段的频闪采样电流和控制占空比曲线放大，如图4所示.在t=7.160 ms开始的频闪周期内，存在，动态特征系数λ=-1，即由稳定状态进入二分岔状态;在下一个频闪周期内动态特征系数，PFC Boost变换器就开始进入发散过程.在经历了一定的频闪周期调整后，PFC Boost变换器由发散的二分岔状态进入混沌状态，电路彻底失稳.

在PFC Boost变换器的输入电压下降段，可定义从理论上的二分岔开始处(=0.5Vo)到调整过程结束电路失稳处的动态特征系数积为失稳的动态特征系数积;由于此时可稳定电路的动态特征系数是逐步振荡增大的，进入混沌时会出现边界碰撞，即出现饱和现象［13］，此时占空比的值为0或1，观察图 4，可见 t=7.820ms开始的频闪周期内D=1，一共经历了38个频闪周期，则失稳的动态特征系数积

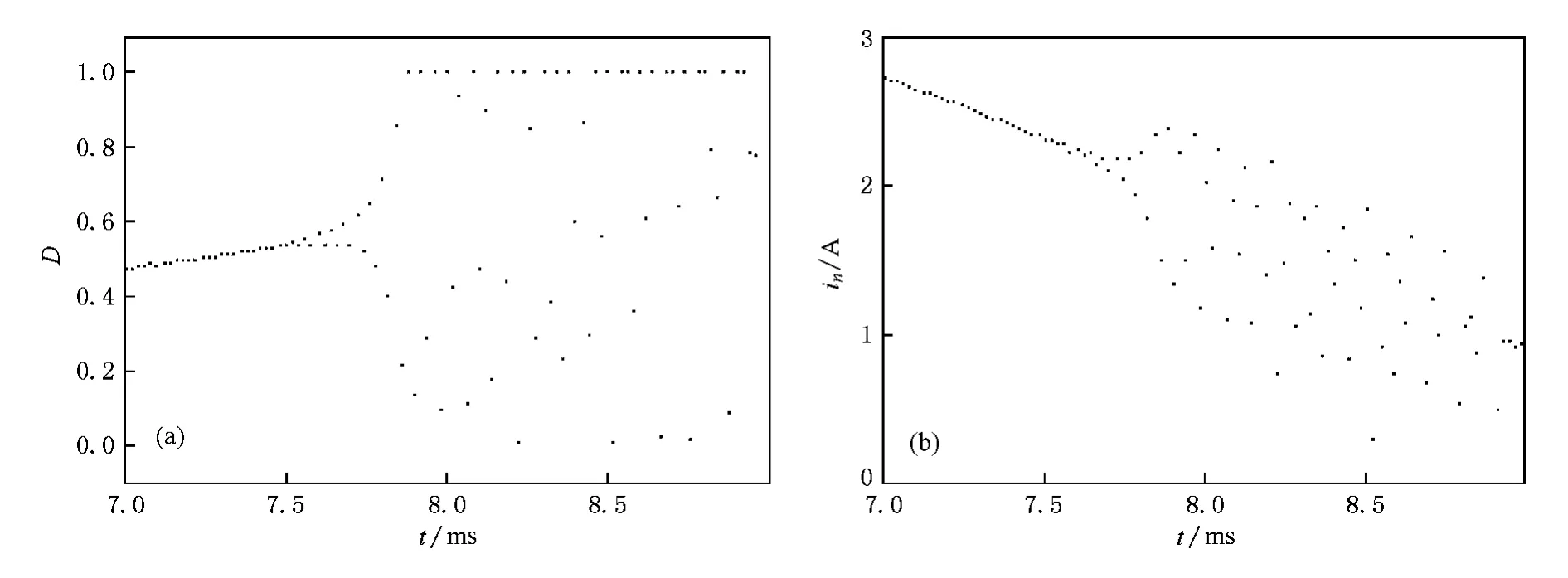
图4 输入电压下降段的快时标不稳定现象 (a)频闪采样占空比，(b)频闪采样时刻的电感电流

综上分析，PFC Boost变换器所出现的快时标不稳定及其不对称现象是由于动态调整过程中的动态镇定能力和调整时间所决定的，输入电压上升段由不稳定区域进入稳定区域的调整过程中，自身较弱的镇定能力通过较长时间的累积才使变换器进入稳定状态;输入电压下降段由稳定区域进入不稳定区域的调整过程中，自身已失去稳定的镇定能力，而具有较微弱的发散能力，也通过较长时间的累积使变换器先进入二分岔发散状态，再进入混沌不稳定状态.动态特征系数在临界分岔点左右的取值不对称，离临界分岔点相同频闪周期距离的点所得的动态特征系数也不互为倒数;等频闪周期距离的点，比较而言，输入电压下降段的动态特征系数绝对值要比上升段的绝对值的倒数略大，说明下降段的发散能力比上升段的收敛能力略强.

3.快时标不稳定的参数共振与正弦化补偿

3.1.参数共振

补偿目的是稳定电路，优化目的是获得较高的功率因数，而功率因数与导通角和 THD(total harmonic distortion)有关.结合 PFC Boost变换器的电路特点，提出一种全局镇定优化的补偿思路，基本思想是通过补偿，在每一个频闪周期内使变换器均具有一定的镇定能力，既存在-1<λn<1，又同时具有正弦化的输入电流.

但是，张恨水先生的文学功底确实为我们敬佩的。从头到尾，文中一直贯穿着的古诗、古情，让我在读的时候不是想尽快知道结果，而是慢慢享受这种韵味儿。这就是所谓的“大家”吧。

参数共振作为一种无反馈的混沌控制，在Boost变换器应用研究较多，可以保证变换器稳定［11，12，14］.由于 Boost电路的混沌和分岔行为对各种电路参数具有很强的敏感性［15］，可选择易于控制的电感电流参考值作为共振参数，共振补偿的动态调整和镇定过程如图1(c)所示，并对部分定义进行改进:定义IRn为第n次频闪采样时刻的电感参考电流值;irn为采用参数斜坡共振的第n个频闪周期内，以IRn为起点的电感参考电流斜坡共振曲线与电感电流曲线的交点，此时电路中的触发器复位;则可得PFC Boost变换器共振调整过程的离散方程

则整理以上等式，可得

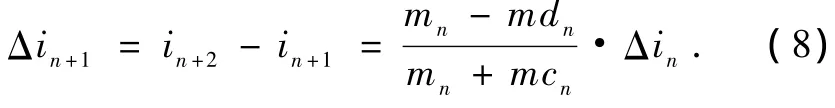
可知相邻两次频闪取样时刻的电感电流差值以系数(mn-mdn)/(mn+mcn)变化，定义参数共振可稳定的PFC Boost变换器的动态特征系数 λn= (mn-mdn)/(mn+mcn)，可得

在可镇定稳定的各频闪周期内取样时刻，电感电流是逐步稳定的，则应趋近于零，则电路稳定条件为 -1<λn<1，则一定的动态特征系数所要求的共振电压为

3.2.正弦化电流补偿

稳定状态下，根据输入输出功率平衡法则，在各个频闪周期内PFC Boost变换器的稳定平衡等式成立［12］，即稳定占空比为

则该频闪周期的电感电流采样值为

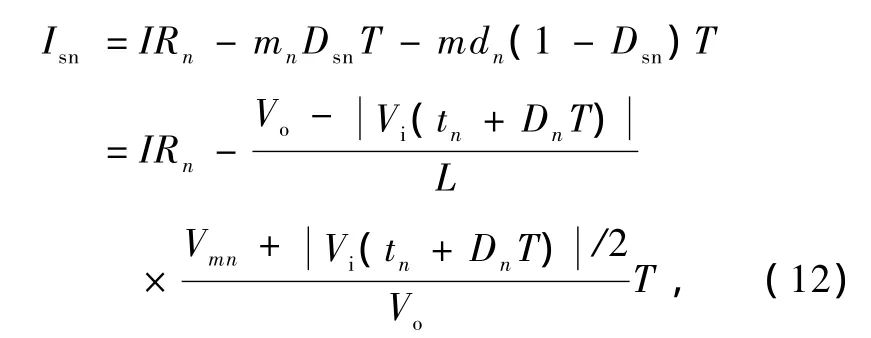
当电感平均电流跟随输入电压正弦波形时，可获得最小的谐波失真，则参考电流为其中IL为PFC Boost变换器的输入电流有效值.

3.3.最强动态补偿

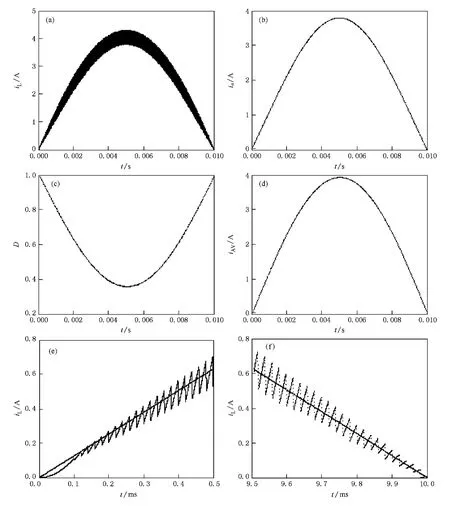
图5 补偿优化后PFC Boost变换器调整过程曲线 (a)优化补偿的电感电流时域曲线，(b)频闪采样时刻的电感电流，(c)频闪采样时刻的控制占空比，(d)电感平均电流，(e)工频周期开始处的电感电流时域曲线，(f)工频周期结束处的电感电流时域曲线

由前面分析可知，没有采用补偿时，电路从每个工频周期开始处经历起动过程，再进入调整过程，必然存在混沌不稳定;若在调整过程中采取补偿技术，使电路具有一定的镇定能力，即动态特征系数，但有限的镇定能力需要经过一段时间才能使电路立即进入稳定，则混沌不稳定现象也必然存在，达不到全工频周期内全局稳定的目的.研究表明［12］，当电感电流斜坡共振电压 Vmn=Vo-时，每个工频周期内的动态特征系数 λ=0时，电路的动态镇定能力最强，共振补偿的斜率和电感电流下降段的斜率相同，电路在当前频闪周期内即可达到稳定，这对于输入电压不断变化的PFC Boost变换器无疑是最理想的控制方法.以动态特征系数λ=0进行补偿优化的结果如图5所示.

通过对仿真结果对比分析可知:采用最优化共振补偿技术不仅消除了快时标不稳定及其不对称现象，还使得电感平均电流呈正弦波形，获得了正弦化的输入电流曲线，总谐波失真度大为降低.与DC-DC Boost变换器的参数微扰不同，正弦化优化补偿策略采用了参数最强共振，可以使 PFC Boost变换器最快速达到稳定，除开始的前6个频闪周期内一直充电以外(如图5(e)所示)，全工频周期内的镇定能力一直保持最强，且在每一个频闪周期内都是稳定的.工频周期内的频闪采样电感电流和控制占空比均稳定，并满足稳态平衡等式，随输入电压的正弦变化而变化.

4.结 论

1)通过定义动态特征系数和动态特征系数积，可以清晰地分析动态调整过程中的动态镇定能力和动态镇定过程，说明电路镇定是动态镇定能力和调整时段联合作用的结果.

2)通过分析输入电压上升段和输入电压下降段的动态特征系数积，说明动态镇定能力是分别从临界分岔点逐渐增强和逐渐减弱的，导致了电路逐步趋稳和逐步失稳，出现了快时标不稳定的左右不对称现象.

3)采用逆向思维，提出电感电流正弦化补偿策略，按照动态调整过程的任意频闪周期内都能稳定的控制要求，采用有最强镇定能力的参数动态共振技术，仿真表明该策略获得了理想的混沌控制结果和补偿效果，可以获得近单位功率因数，提高电路转换效率.

［1］Dranga O，Tse C K，IU H C H 2003 Int.J.Bifurcat.Chaos 13 3107

［2］Orabi M，Ninomiya T 2003 IEEE Transactions on Industrial Electronics 50 1116

［3］Tse C K 2003 Int.J.Circuit Theor.Appl.31 157

［4］IU H C H，Zhou Y F，Tse C K 2003 Int.J.Circuit Theor. Appl.31 611

［5］Tse C K，Dranga O，IU H C H 2003 Proceedings of IEEE International Symposium on Circuits and Systems 3 312

［6］Wu X Q，Tse C K，Dranga O 2005 Proceedings of IEEE International Symposium on Circuits and Systems 2477

［7］Ren H P，Liu D 2005 Chin.Phys.14 1352

［8］Ma X K，Liu W Z，Zhang H 2005 Proceeding of the CSEE 25 619(in Chinese)［马西奎、刘伟增、张 浩2005中国电机工程学报25 619］

［9］Wu X Q，Tse C K，Dranga O 2006 IEEE Transactions on Circuits and Systems 53 204

［10］Zhou J L，Ma X K 2008 Proceeding of the CSEE 28 38(in Chinese)［邹建龙、马西奎2008中国电机工程学报28 38］

［11］Zhou Y F，Huang J C，Wang S B，Jiang W，Chen J N 2009 Sci.Chin.(Ser F)39 1217(in Chinese)［周宇飞、黄家成、王诗兵、江 伟、陈军宁2009中国科学-F辑39 1217］

［12］Cheng W B，Guo Y N，Tang N，Huo A Q，Wang Y L，Kang S M 2010 Acta Phys.Sin.59 3035(in Chinese)［程为彬、郭颖娜、汤 楠、霍爱清、汪跃龙、康思民2010物理学报59 3035］

［13］Zou J L，Ma X K 2008 Acta Phys.Sin.57 720(in Chinese)［邹建龙、马西奎2008物理学报57 720］

［14］Cheng W B，Guo Y N，Kang S M，Wang Y L，Huo A Q，Tang N 2009 Acta Phys.Sin.58 4439(in Chinese)［程为彬、郭颖娜、康思民、汪跃龙、霍爱清、汤 楠2009物理学报58 4439］

［15］Cheng W B，Fu Z W，Zhong Y R 2008 Chin.J.Mech.Eng. 44 246(in Chinese)［程为彬、傅钟炜、钟彦儒2008机械工程学报44 246］

PACS:05.45.-a，05.45.Gg，05.45.Pq

Fast-scale instability and dynamic parameter resonance of power factor correction Boost converter*

Cheng Wei-BinKang Si-Min Wang Yue-Long Tang Nan Guo Ying-Na Huo Ai-Qing
(School of Electronic Engineering，Xi'an Shiyou University，Xi'an 710065，China)

5 May 2010;revised manuscript

3 June 2010)

Based on the multiplication of dynamic eigenvalue coefficient and its dynamic stabilizing capability，fast-scale instability and its asymmetry in power factor correction(PFC)Boost converter with continuous peak current control mode are investigated.To realize higher power factor and less harmonic distortion，a kind of compensation strategy is proposed to make the input current a sinusoidal wave，and it is optimized with parameter resonance.The formulas are deduced，and the overall optimization is carried out.The results of digital simulation shows that the overall compensating strategy has the most powerful dynamic ability to ensure the quick stabilization during every stroboscopic period，and the fast-scale instability is controlled，and the approximate unit power factor and the best compensating effects are obtained finally，resulting in the increase of the conversion efficiency of PFC Boost converter.

Boost converter，power factor correction，fast-scale instability，parameter resonance

*国家高技术研究发展计划(批准号:2003AA602013)，陕西省自然科学基础研究计划(批准号:SJ08E216)和陕西省教育厅科研专项基金(批准号:08JK410，09JK687)资助的课题.

*Project supported by National High Technology Research and Development Program of China(Grant No.2003AA602013)，the Natural Science Foundation of Shaanxi Province，China(Grant No.SJ08E216)，and the Specialized Research Fund for Shaanxi Province Education Department，China(Grant Nos.08JK410，09JK687).