井底压差对岩石破碎的影响机制

郑德帅,高德利,张 辉

(中国石油大学石油工程教育部重点实验室,北京102249)

井底压差对岩石破碎的影响机制

郑德帅,高德利,张 辉

(中国石油大学石油工程教育部重点实验室,北京102249)

综合地层应力、井底压力、孔隙压力以及牙齿吃入地层引起的应力,建立牙齿吃入深度的表达式,依据摩尔-库伦准则建立钻头牙齿吃入地层的岩石破碎模型。将综合地层和钻井参数因素的误差函数β与深度x的比值作为欠平衡钻井的应用参考参数,计算各种压差和β/x条件下的吃入深度,并分析其变化规律。结果表明:在压差的作用下,具有渗透率和孔隙度的待破碎薄地层内的孔隙压力并非原始地层孔隙压力,而是随时间和位置的变化而变化,其分布规律可以用一维不稳定渗流来表示和计算;牙齿吃入深度的表达式可以将压力、流体等因素对岩石破碎的作用清楚地表达出来;所建模型可以解释欠平衡钻井提高钻速的力学机制,以及定量描述随钻地层压力监测dc指数法的适用范围。

压差;岩石破碎;地层压力;欠平衡钻井;dc指数法

钻井液或气体(统称钻井流体)在井底的压力与地层孔隙压力往往不等,两种压力之间的差值对于井底岩石的破碎效率有着重要的影响。dc指数法就是据此利用钻时资料随钻监测地层压力,但其应用范围和精度往往受到岩性及钻井参数的限制[1-2]。因此,有必要要对井底压差和钻时之间的关系进行机制探讨,以便对其应用范围进行科学界定。欠平衡钻井产生的负压差可以大幅度提高钻速,但某些井段的提速效果却并不明显[3],这也是对井底压差的影响机制不清楚所致。对于井底压差与钻时的关系,杨进等[4]通过现场所得数据进行拟合分析,得到了一个函数关系模型;李洪乾等[5]认为压差的增大使得岩石的抗破碎强度增加,并且导致岩石塑性增大,降低了钻头的破碎效率;黄建林等[6]指出在高密度钻井流体条件下,破碎体积仅为正常密度条件下的1/2～1/3。目前压差与钻时关系的研究大多以试验结果描述或现场数据拟合为主[7-9],对于井底压力与地层压力影响岩石破碎效率的力学机制并不清楚。由于岩石本身的多孔介质渗透性以及受到压差的作用,待破碎岩石内部的孔隙压力并非原始地层压力,而是会随着时间和距离的变化而变化[10-11]。对钻速产生影响的压差与岩性和钻井参数有关。笔者假设井底水力充足,只研究岩石在压差作用下的破岩机制,暂不考虑压差导致的岩屑重复破碎(压持效应)等因素。采用一维不稳定渗流模型来描述实际地层孔隙压力随时间与距离变化的规律,并综合井底各种应力建立岩石破碎模型。

1 地层孔隙压力的分布

井底待破碎岩石中的孔隙压力是影响岩石破碎的重要因素,当钻开井眼以钻井流体柱代替原有的岩石柱后,地层孔隙压力pp0与钻井流体压力pm一般并不相等,这样就会出现名义压差Δp,即

在远离井底平面的地层中,孔隙压力几乎不受压差的影响,但是对于钻头破碎而言,其破碎的对象只是井底较薄的一层岩石,每次破碎的厚度只有几个毫米。在具有一定渗透率的近井底薄层中,压差作用使钻井流体与地层孔隙流体之间发生相互流动,井底待破碎薄层中的孔隙压力随之出现变化,实际压差并不等于名义压差,这种变化与离井底平面的距离x和时间t这两个因素有关,x如图1所示。根据渗流力学原理,上述作用可以用一维不稳定渗流的基本微分方程[8]表示为

式中,x为深度位置坐标,m;t为时间,s;pp为井底地层压力,是一个随x和t变化的函数,MPa;k为岩石渗透率,m2;μ为井流体黏度,Pa·s;φ为地层孔隙度;C为岩石和流体总的可压缩系数。

图1 井底受力图Fig.1 Forces on bottom hole

根据边界条件及偏微分方程可以求出地层孔隙压力随时间与位置的变化,表达式如下:

其中

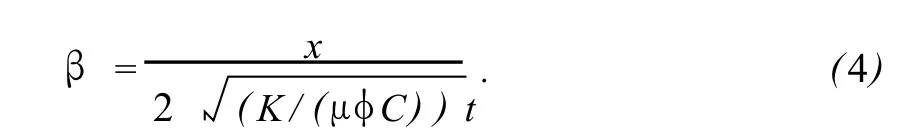
公式(3)中包含β的积分部分在数学上称之为误差函数,难以积分出解析的表达式,这是一种专门的数学函数,可以通过数学手册查找不同β对应的值。其中的β表达式(4)可以容易地计算出来,由于β与深度x成正比,而深度往往为自变量或待求值,与β相互影响。所以,引入与x无关的β/x,并将其定义为地层、流体以及时间等参数对井底压差作用范围的影响因子。

假设钻井流体黏度μ=0.01 Pa·s,岩石孔隙度φ=0.2,总压缩系数C=4.34×10-10,时间t=0.5 s,原始地层压力pp0=20 MPa,井底钻井流体压力pm=25.5 MPa。计算出的不同岩石渗透率1.2×10-16、1.2×10-17、1.2×10-18m2,对应的β/x取值分别为59、189、598条件下不同深度的地层压力见图2。

图2 地层因素对于地层压力分布的影响Fig.2 Effect of formation on pore pressure distribution

图2表明,在离井底一定距离内地层流体压力并非原始地层孔隙压力,而是随着x的变化而变化,当x增大到一定值后,实际的地层流体压力才逐渐趋向于原始地层孔隙压力。较低的地层渗透率或黏度较大的流体会阻碍流体交换,压差对地层的影响范围较小,待破碎地层中的实际地层流体压力由井底钻井流体压力很快趋向于原始地层孔隙压力;随着地层渗透率的增大,压差可以影响到离井底较远的区域。

2 井底受力

井底处于地层的围压pf、钻井流体压力pm及地层孔隙压力pp等诸种压力作用之下,钻头牙齿吃入地层后在局部又会形成应力分布,故井底岩石破碎应考虑这些因素的影响。

假设岩石剪切破坏面与井底平面夹角为θ(如图1),则在此破坏面上,各种压力产生的剪切力和法向力可表达为

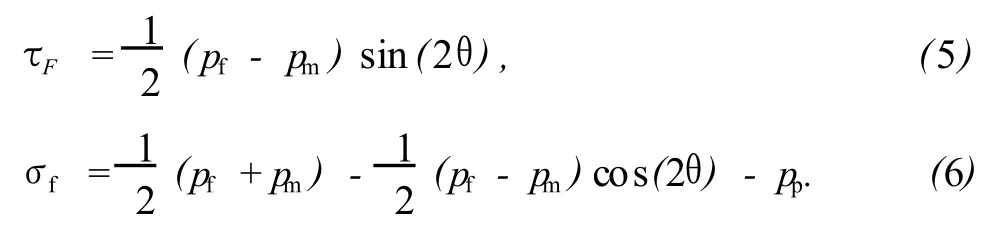
当pm很小时,就可以计算空气钻井时的情况。由于破碎面是从井底某一深度到井底平面,pp是一个随破坏面位置变化的函数,为简单起见,可取破坏面两端地层压力的平均值

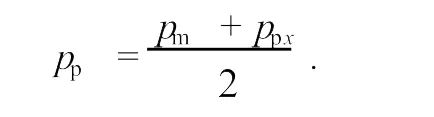
式中,ppx为深度为x处的流体压力。破坏面另一端就是井底表面,其流体压力应等于井底钻井流体压力pm。

假设每个牙齿承受的力为F,牙齿本身的尖角为2α,吃入深度为h,剪切破坏面的长度L和牙齿表面上的力R可表达为

牙齿表面上的力R在破坏面上产生的剪应力及法向应力为

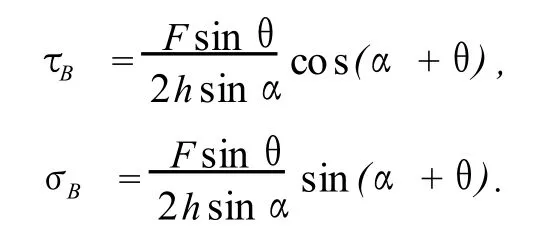
显然,卸载相关条件下的剪切破坏面的剪力和法向应力可分别表达为

可采用摩尔-库伦准则作为井底岩石的破坏判据,即有

将公式(7)、(8)代入(9),整理后可得

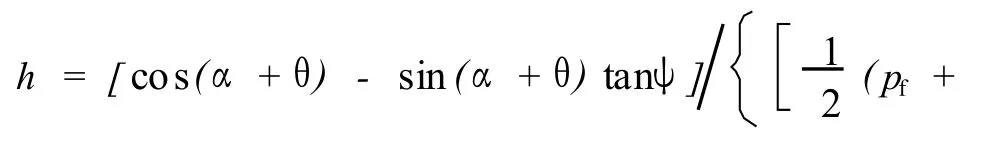
牙齿吃入深度与机械钻速的关系最为密切,各因素对吃入深度的影响可以反映出对机械钻速的影响。式(10)为牙齿吃入地层深度的表达式,综合考虑了牙齿受力、牙齿形状、地层孔隙压力、地应力、井底钻井流体压力、岩石强度、地层渗透率、钻井流体黏度及可压缩系数诸多等因素的影响。

式(10)中显示地层孔隙压力影响吃入深度,而式(3)表明牙齿吃入深度会影响待破碎岩石的流体压力分布,可见两者相互影响。考虑到式(10)的复杂性及式(3)涉及非基本函数,本文中采用计算机编程来计算最终的吃入深度。计算步骤如下:

(1)先假设实际地层流体压力为原始地层孔隙压力pp0,利用式(10)计算h1;

(2)利用h1及式(3)计算待钻地层流体压力pp1(h1,t);

(3)取地层流体压力pp1(h1,t),再利用式(10)计算h2;

(4)计算Δh=h1-h2,如果Δh小于某一预设值,则认为h2为最终吃入深度,否则,返回到计算步骤(2),并让h取值h2循环计算,直至满足计算精度。

3 应用分析

假设岩石的内聚力cθ=25 MPa和内摩擦角为25°,地层围压为40 MPa,地层孔隙压力为20 MPa,牙齿受力50 kN,θ=30°,α=5°,β/x取值与图2相同。根据以上数据和式(10),就可以计算不同Δp及β/x条件下的牙齿吃入深度,结果见图3和图4。

图3 名义压差与吃入深度的关系Fig.3 Relation of differential pressure and invasion depth

由图3可见,随着压差的增大,吃入深度减小,这就说明在转速一定的条件下,机械钻速将下降,而在欠平衡负压差条件下,吃入深度大幅度增加。这就解释了欠平衡钻井尤其是气体钻井(负压差更大)可以大幅度提高钻速的原因。

图4 影响因子β/x与吃入深度的关系Fig.4 Relation of influence factorβ/x and invasion depth

但也要注意到,在不同β/x的条件下,吃入深度随压差的变化幅度是不同的。这就意味着,在实施包括充气钻井这类只能产生较小负压差的欠平衡钻井技术的时候,要考虑到地层因素的影响,当β/x值很小的时候,主要由于高渗透率的作用,实际压差要小于名义压差,提速的效果就会减弱,这也解释了有些充气钻井提速并不明显的原因,因此低渗地层更有利于实施欠平衡钻井。

影响实际压差的因素除了地层渗透率之外,距离井底的长度也是重要的因素。从图2可以看出,距离井底越远,实际的压差就越大,而增大钻压可以使牙齿吃入到更深的位置,从而使实际压差增大,相当于起到了低渗地层的作用,因此增大钻压可以加强欠平衡钻井提速的效果。

由图4看以看出,当β/x小于一定值(大约300)时,吃入深度是不稳定的,随着β/x的变化而变化,而当β/x大于一定值时,吃入深度固定下来,与β/x的变化关系很小,而只与压差有关。这就说明,当使用dc指数法随钻检测地层孔隙压力时,最好选取β/x大于300,这时钻速的变化受压差影响最大,反演地层孔隙压力的结果也最为准确。当β/x较小时,影响钻速的因素可能不只是压差,还包括岩性变化,如果用这种情况下钻速的变化反演地层孔隙压力,结果将不甚准确。

dc指数法的使用经验表明,在渗透率较低的泥页岩效果较好,而在轻压吊打条件下则不宜使用dc指数法,根据公式(4),渗透率降低会增大β/x,根据上面的分析,小的机械钻速相当于降低了β/x值,因此,理论的分析与经验是一致的,而且提供了明确的指标。

4 结 论

(1)在压差的作用下,具有渗透率和孔隙度的待破碎薄地层内的孔隙压力并非原始地层孔隙压力,而是随时间和位置的变化而变化,其分布规律可以用一维不稳定渗流来表示。

(2)综合地层应力、井底压力、孔隙压力以及牙齿吃入地层引起的应力建立的牙齿吃入深度的表达式,较好的解释了欠平衡、气体钻井提高钻速的原因。综合地层和钻井参数因素的β/x值可以作为欠平衡钻井应用的参考参数。

(3)通过分析各种压差条件下吃入深度随β/x的变化规律,为随钻检测地层压力的dc指数法提供了明确的适宜应用范围,从而提高了dc指数法的准确性。

[1] 杨进,高德利.地层压力随钻检测新方法及其应用[J].石油钻探技术,1998,26(2):16-19.YANG Jin,GAO De-li.A new method of formation pore pressure detection while drilling and its application[J].Petroleum Drilling Techniques,1998,26(2):16-19.

[2] 冯顺利,王东.直线平移dc指数法计算地层压力在S84井中应用[J].西部探矿工程,2006,125(9):85-88.FENG Shun-li,WANG Dong.Applications of offset dc method in S84 well for pore pressure calculation[J].West-China Exploration Engineering,2006,125(9):85-88.

[3] 艾贵成,穆辉亮,王卫国,等.充气钻井液技术在清西油田的应用[J].吐哈油气,2008,13(2):170-173.A I Gui-cheng,MU Hui-liang,WANG Wei-guo,et al.Application of aerated drilling fluid technique in Qingxi Oilfield[J].Tuha Oil&Gas,2008,13(2):170-173.

[4] 杨进.岩石抗钻强度与地层压力关系模型及其应用[J].石油大学学报:自然科学版,2001,25(2):1-5.YANG Jin.Correlation model of rock strength and formation pore pressure and its application[J].Journal of the University of Petroleum,China(Edition of Natural Science),2001,25(2):1-5.

[5] 李洪乾,杲传良,任耀秀.压差对机械钻速的影响规律[J].钻采工艺,1995,18(2):10-15.L I Hong-qian,GAO Chuan-liang,REN Yao-xiu.Rules of effects of differential pressure on ROP[J].Drilling&Production Technology,1995,18(2):10-15.

[6] 黄建林,马飞,刘伟,等.川西深层须家河组气藏提高钻速对策及实践[J].钻采工艺,2006,29(6):16-18.HUANG Jian-lin,MA Fei,L IU Wei,et al.Strategy and practice for improving drilling speed in the deep gas reservoir of Xu-jiahe group in west Sichuan basin[J].Drilling&Production Technology,2006,29(6):16-18.

[7] 楼一珊,陈勉,史明义,等.岩石Ⅰ、Ⅱ型断裂韧性的测试及其影响因素分析[J].中国石油大学学报:自然科学版,2007,34(4):85-89.LOU Yi-shan,CHEN Mian,SH IMing-yi,et al.Measurement of type-Ⅰand type-Ⅱfracture toughness for rocks and its influence factors analysis[J].Journal of China U-niversity of Petroleum(Edition of Natural Science),2007,34(4):85-89.

[8] 徐依吉,赵红香,孙伟良,等.钢粒冲击岩石破岩效果数值分析[J].中国石油大学学报:自然科学版,2009,33(5):68-72.XU Yi-ji,ZHAO Hong-xiang,SUN Wei-liang,et al.Numerical analysis on rock breaking effect of steel particles impact rock[J].Journal of China University of Petroleum(Edition of Natural Science),2009,33(5):68-72.

[9] 陈德春,孟红霞,黄新春,等.岩石动态损伤模拟实验装置的研制[J].中国石油大学学报:自然科学版,2007,31(3):77-81.CHEN De-chun,MENG Hong-xia,HUANG Xin-chun,et al.Development of experimental apparatus of simulation for rocks dynam it damage[J].Journal of China University of Petroleum(Edition of Natural Science),2007,31(3):77-81.

[10] 尹兆娟,杨继峰,崔超.井底岩石压差的扩散特点及提高钻速研究[J].石油化工和设备,2009(7):14-19.Y IN Zhao-juan,YANG Ji-feng,CU I Chao.Diffusion characters for differential pressure and drilling performance enhancement[J].Petroleum Chemistry and Equipment,2009(7):14-19.

[11] DETOURNAY E,ATK INSON C.Influence of pore pressure on the drilling response in low-per meability shear-dilatants rocks[J].International Journal of Rock Mechanics&Mining Sciences,2000(37):1091-1101.

(编辑 修荣荣)

Mechanism for effect of down hole differential pressure on rock failure

ZHENG De-shuai,GAO De-li,ZHANG Hui

(MOE Key Lab of Petroleum Engineering in China University of Petroleum,Beijing102249,China)

Based on the stresses in formation including drilling fluid pressure at down hole,pore pressure and stress caused by teeth invasion,the expression of teeth invasion depth was developed,and rock failure model for teeth invasion was established according to Morh-Coulomb principle.Using the ratio of error function and depthxas the reference parameters for under balanced drilling application,invasion depths under all kinds of differential pressures andβ/xwere calculated,and the variation law was analyzed.The calculation results show that the real pore pressure of formation near down hole is not the original pore pressure because rock has permeability and porosity.The real pore pressure is related with time and location,and its distribution law can be expressed by one dimension unstable filtration theory.The expression of teeth invasion depth can clearly demonstrate respective effect of pressures and fluid on rock failure.This model can explain the mechanism of enhanced rate of penetration in under balanced drilling,and it can depict the scope of application for dc index method correctly.

differential pressure;rock failure;formation pressure;under balanced drilling;dc index method

TE 21

A

10.3969/j.issn.1673-5005.2011.02.012

2010-06-10

国家“973”研究课题(2010CB226703)

郑德帅(1983-),男(汉族),山东五莲人,博士研究生,主要研究方向为油气井井下控制与岩石力学方面的研究。

1673-5005(2011)02-0069-05