基于有限元的低渗透油藏水平井试井分析

樊冬艳,姚 军,王子胜

(中国石油大学石油工程学院,山东青岛266555)

基于有限元的低渗透油藏水平井试井分析

樊冬艳,姚 军,王子胜

(中国石油大学石油工程学院,山东青岛266555)

针对低渗透油藏渗流普遍存在启动压力梯度的特点,建立考虑启动压力梯度的盒状油藏水平井不稳定渗流数学模型。利用伽辽金有限元方法得到水平井井底压力数值解,并与经典的Odeh解析解对比验证本数值算法的正确性。结果表明:启动压力梯度存在时,水平井压力及压力导数曲线都呈上翘趋势,且启动压力梯度越大,曲线上翘越明显,即所需压差越大;启动压力梯度对压力导数的影响是一个逐渐抬升的过程,与压力波传播到周围边界而引起的曲线上升有着本质上的不同。

水平井;低渗透油藏;启动压力梯度;有限元方法;试井分析

国内外大量的室内试验和矿场实践表明,低渗透油藏中的渗流不符合经典的达西定律,而存在启动压力梯度[1-4]。姚军等[5-6]得出启动压力梯度对低渗透油藏水平井产能有较大影响的结论,而国内外对水平井试井解释理论的研究几乎都没有考虑启动压力梯度的影响[7-12]。因此,笔者在前人研究的基础上,建立存在启动压力梯度的水平井试井解释数学模型,利用有限元方法进行数值求解,与经典的Odeh解析解进行对比,验证数值算法的准确性并进行动态分析。

1 渗流模型的建立

1.1 物理模型

盒状油藏内有一水平井,如图1所示。油藏在x、y、z3个方向的长度分别为a、b、h,水平井长度为L。

假设:盒状油藏均质各向异性,各方向渗透率分别为kx、ky和kz;油藏外边界封闭,中部有一口与顶、底面平行的水平井;水平井以定产量生产,沿着水平井长度流量均匀分布,压力非均匀分布;岩石和流体均微可压缩,且压缩系数为常数;流体遵循具有启动压力梯度的非达西渗流规律。

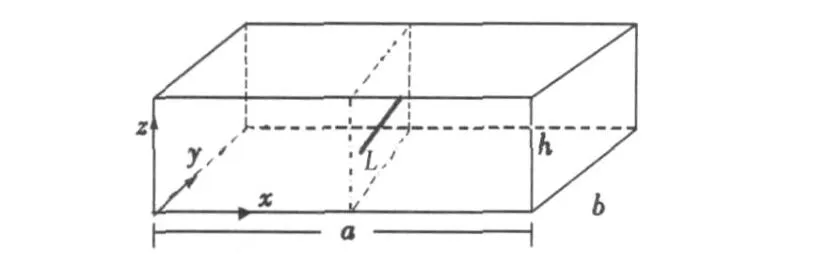
图1 盒状油藏一水平井示意图Fig.1 Schetch map of a horizontal well in box-shaped reservoir

1.2 数学模型

流体服从具有启动压力梯度的非达西流,运动方程为

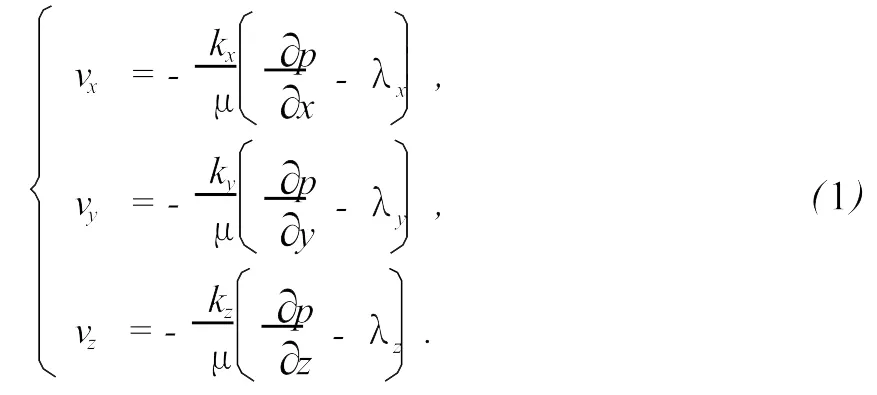
式中,λx、λy、λz分别为x、y、z方向的启动压力梯度,10-1MPa/s;vx、vy、vz分别为原油在x、y、z方向的流速,cm/s;μ为原油黏度,mPa·s;p为井底压力,10-1MPa。

∂p/∂l(l=x、y、z)与λl同号,说明由于启动压力梯度的作用使得渗流速度降低。

状态方程为

式中,φ为地层孔隙度,%;ρ为原油密度,g/cm3;pi为原始地层压力,10-1MPa;φ0和ρ0分别为原始地层压力下的地层孔隙度和原油密度;CL和Cp分别表示流体和孔隙的压缩系数,10 MPa-1。

连续性方程为

式中,q为单位时间单位体积内采出的流体体积,s-1。

把水平井考虑为三维空间中的线源,以盒状油藏的顶点为原点建立坐标系,则水平井两个端点的坐标为(a/2,b/2-L/2,h/2)和(a/2,b/2+L/2,h/2),水平井上任一点的坐标为(a/2,y′,h/2),其中b/2-L/2≤y′≤b/2+L/2。把式(1)、(2)代入式(3)得到低渗透油藏的扩散方程为

式中,Ct为综合压缩系数,10 MPa-1。

初始条件为

边界条件为

若假定kx=ky=kh,kz=kv,令

则低渗透油藏水平井试井解释数学模型变为

以上方程中q是指水平井任一点的流量,考虑水平井为均匀流量下的线源,故水平井的总流量Q=qL。

2 数学模型的求解

应用Galerkin(伽辽金)方法推导有限元积分方程,时间上采用向后差分方式。选择四面体单元作为母单元,并采用二次插值函数,其中4个角点和6个棱内中点作为单元的节点,对于每个单元e的压力可用这10个节点处的值表示为

其中

式中,Ni为单元上的二次插值函数;Li(i=1,2,3,4)为顶点的面积坐标。

图2所示为每个单元的节点排序,油藏节点的整体排序按优化带宽的原则来处理。

图2 四面体单元示意图Fig.2 Sketch map of tetrahedron element

单元特性分析:

外边界封闭,则

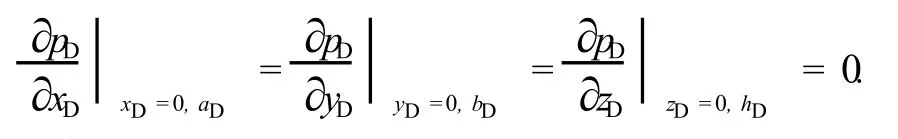
于是单元e的有限积分方程为

对于i=1,2,…,10写成矩阵的形式为

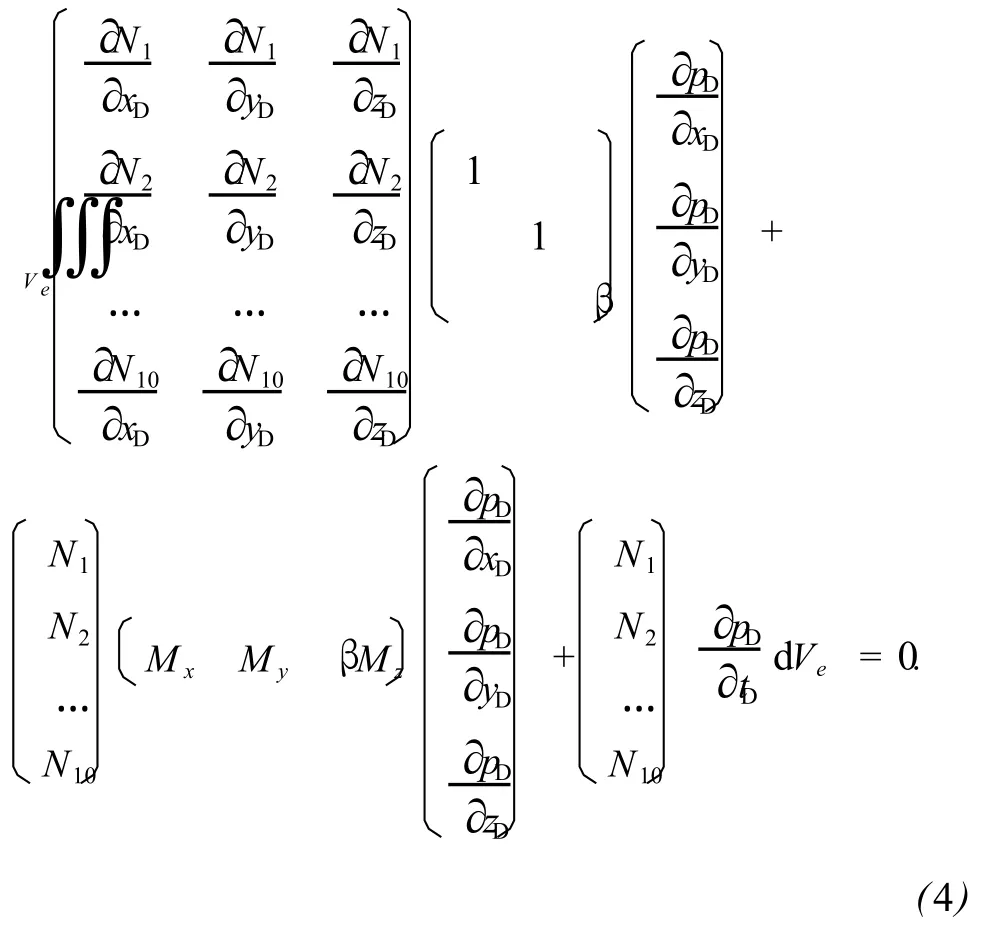
其中

令

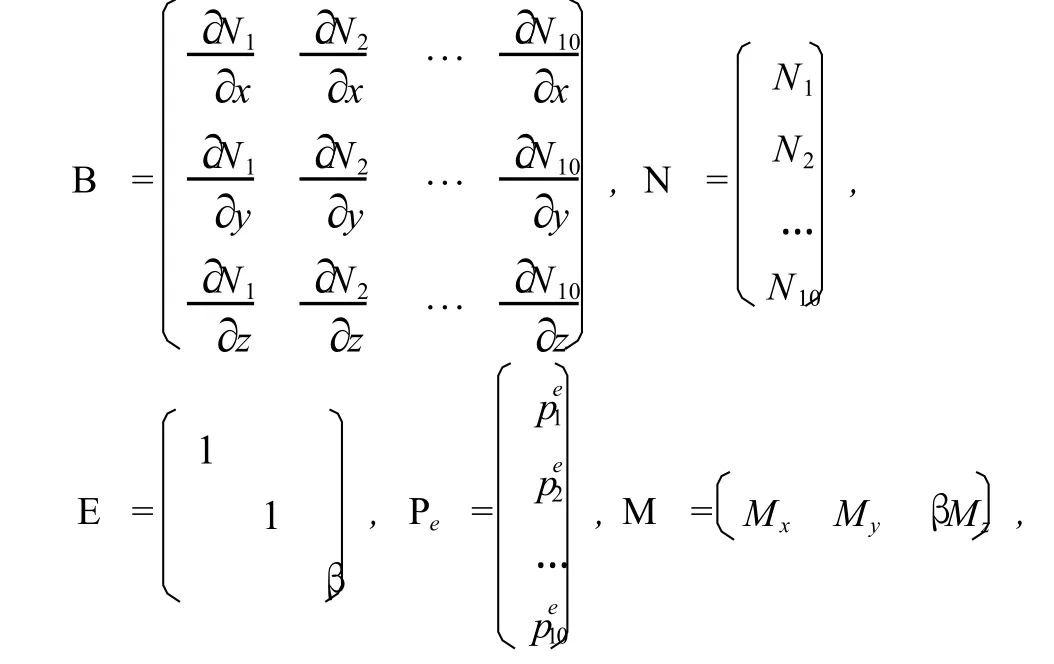
则式(4)转化为

假定

则单元方程组转化为

存在源汇项的单元方程组为

其中

通过组装整体矩阵和列阵,建立相应的整体方程组,求解方程组便能得到各个时刻的压力值。为了保证计算精度,需对水平井周围的网格进行加密处理,同时为了减少计算工作量,时间采用指数形式递增。

3 计算结果的对比验证及分析

水平井采用的是均匀流量模型,所以沿水平井筒上各处的压力不完全相等,一般取yD=0.7L处的压力作为水平井底的压力值[13]。

3.1 数值算法正确性验证

为了验证本算法结果的正确性,不考虑启动压力梯度,与常用经典的Odeh模型解析解进行对比。对Odeh模型[7-8]进行相应的无因次化处理,作典型曲线,如图3所示。油藏和水平井参数取值为aD=12,bD=12,hD=0.2,LD=1。由图3可见该模型在没有考虑启动压力梯度情况下与Odeh解析解计算结果吻合得很好,说明该数值算法切实可行。

图3 本文模型与Odeh模型压力及压力导数曲线对比Fig.3 Comparison of pressure and pressure derivative responses between thismodel and Odeh model

3.2 启动压力梯度对水平井压力响应的影响

考虑启动压力梯度的影响,油藏和水平井参数取值同上,油藏各向同性,即β=1。不同无因次启动压力梯度下低渗水平井井底压力动态如图4所示。

图4 不同启动压力梯度时水平井压力及压力导数曲线Fig.4 Effect of TPG on pressure and pressure derivative curves for horizontal well

由图4可见水平井的基本流动形态分为早期径向流、早期线性流、晚期拟径向流以及到达边界以后的拟稳态流动。此时aD=bD,压力波几乎同时到达周围边界,故没有出现晚期的拟线性流。当启动压力梯度存在时,压力及压力导数曲线都表现出上翘趋势,时间越长,与不考虑启动压力梯度曲线相差越明显;当启动压力梯度(M)越大时,压力与压力导数曲线上翘越厉害,定产量生产时所需井底压差就越大。

3.3 启动压力梯度与边界的影响

由于启动压力梯度的影响主要表现在后期,与盒状油藏封闭边界对压力的影响类似,但这两个因素对压力响应的影响又完全不同。如图5所示,首先,启动压力梯度对压力响应的影响是一个持续的过程,在晚期表现得更为明显,故它呈现的是一个逐步上翘的曲线,时间越长曲线偏离得越厉害。但是,如果压力波传播到周围边界,当aD=bD时,压力波同时到达边界,不存在晚期的拟线性流动阶段,从晚期拟径向流直接进入拟稳态流动,在压力导数曲线上表现为直线斜率由0直接过渡到斜率为1;当aD≠bD时,水平井在进入拟稳态之前会出现晚期的拟线性流,再过渡到拟稳态流动,在压力导数曲线上表现为由斜率0的直线过渡到斜率为1/2的直线,再最后过渡到斜率为1的直线。

图5 启动压力梯度影响与边界影响下压力导数曲线对比Fig.5 Comparison of effect of TPG and reservoir boundary on pressure derivative curves

4 结 论

(1)低渗透油藏启动压力梯度存在时,水平井压力及压力导数曲线都表现出上翘趋势;启动压力梯度越大,曲线上翘越厉害,即定产量生产时井底所需压差就越大。启动压力梯度对压力导数曲线是一个持续影响的过程,与压力波到达边界产生的压力导数曲线上翘原理完全不同。

(2)考虑启动压力梯度的影响,不能直接利用Duhanmel原理考虑井筒存储系数和表皮效应的影响。考虑启动压力梯度的变流量情况下的压力公式需要进一步研讨。

[1] 戈尔布诺夫A T,张树保.异常油田开发[M].北京:石油工业出版社,1987.

[2] 闫存章,李阳.低渗透油田开发技术文集[M].北京:石油工业出版社,2008.

[3] 徐绍良,岳湘安.低速非线性流动特性的实验研究[J].中国石油大学学报:自然科学版,2007,31(5):60-63.XU Shao-liang,YUE Xiang-an.Experimental research on nonlinear flow characteristics at low velocity[J].Journal of China University of Petroleum(Edition of Natural Science),2007,31(5):60-63.

[4] 熊伟,雷群,刘先贵,等.低渗透油藏拟启动压力梯度[J].石油勘探与开发,2009,36(2):232-236.X IONG Wei,LEI Qun,L IU Xian-gui,et al.Pesudo threshold pressure gradient to flow for low permeability reservoirs[J].Petroleum Exploration and Development,2009,36(2):232-236.

[5] 姚军,刘顺,胥元刚.低渗透油藏水平井流入动态关系的建立[J].中国石油大学学报:自然科学版,2008,32(4):64-72.YAO Jun,L IU Shun,XU Yuan-gang.Establishment of inflow performance relationship of horizontal wells in lowper meability reservoir[J].Journal of China University of Petroleum(Edition of Natural Science),2008,32(4):64-72.

[6] 赵静.低渗透油藏水平井流入动态及影响因素[J].西南石油大学学报:自然科学版,2009,31(2):90-92.ZHAO Jing.Inflow performance and affecting factor of horizontal wells in low permeability reservoir[J].Journal of Southwest Petroleum Unversity(Science&Technology Edition),2009,31(2):90-92.

[7] BABU D K,ODEH Aziz S.Productivity of a horizontal well[R].SPE 18298,1989.

[8] BABU D K,ODEH Aziz S.Appendices A and B of SPE18298[R].SPE 18334,1989.

[9] ODEH Aziz S,BABU D K.Transient flow behavior of horizontal wells:pressure drawdown and buildup analysis[R].SPE 18802,1990.

[10] ISSAKA M B,AMBASTHA A K.Drawdown and buildup pressure deriwative analyses for horizontal wells[R].SPE 24323,1992.

[11] 姚军,李爱芬,陈月明,等.盒状砂岩油藏中水平井试井分析方法[J].石油学报,1997,18(3):105-109.YAO Jun,L IAi-fen,CHEN Yue-ming,et al.Transient pressure analysis for horizontal well in box-shaped reservoir[J].Acta Petrolei Sinica,1997,18(3):105-109.

[12] 王德山,李兆敏,聂立新.水平分支井试井解释方法研究[J].西南石油大学学报:自然科学版,2007,29(1):70-74.WANG De-shan,L I Zhao-min,N IE Li-xin.Well test interpretation method for horizontal multilateral wells[J].Journal of Southwest Petroleum Unversity(Sicence&Technology Edition),2007,29(1):70-74.

[13] DAV IAU F,MOURONVAL G,BOURDAROT G,et al.Pressure analysis for horizontal wells[R].SPE 14251,1988.

(编辑 李志芬)

Horizontal well testing analysis in low-permeability reservoirs based on finite element method

FAN Dong-yan,YAO Jun,WANG Zi-sheng

(College of Petroleum Engineering in China University of Petroleum,Q ingdao266555,China)

Considering the threshold pressure gradient(TPG)phenomenon in low-permeability reservoirs,a mathematical unsteady flow model of horizontal well with TPG was established in box-shaped reservoir.The numerical solution of bottom pressure of horizontal well was obtained by using the Galerkin finite element method,which was verified by comparing with the classic Odeh solution.The results show that the horizontal well pressure and its derivative curves present an upward tendency when the TPG is considered.And the bigger the TPG,the more severe the curves upturned,namely,the greater pressure difference is required.Meanwhile,the effect of TPG on pressure derivative increases gradually,which is essentially different from the curve upturned when the pressure reaches the surrounding boundary.

horizontal well;low-per meability reservoir;threshold pressure gradient;finite element method;well testing analysis

TE 353

A

10.3969/j.issn.1673-5005.2011.02.014

2010-05-20

国家“973”重点基础研究发展计划项目(2006CB202400)

樊冬艳(1985-),女(汉族),江西南昌人,博士研究生,主要从事低渗透油藏水平井渗流理论及试井分析研究。

1673-5005(2011)02-0080-05