反向旋转双转子系统动力学特性的有限元分析
2011-09-27王克明艾书民
缪 辉,王克明,翟 学,艾书民
(沈阳航空航天大学动力与能源工程学院,辽宁 沈阳 110136)
早在上世纪50年代,反向旋转双转子结构就被应用于军用发动机的设计。英国的罗尔斯·罗伊斯公司为“鹞”式战斗机最先研制了“飞马”反向旋转双转子发动机。由于高、低压转子反向旋转,它可以适当消除陀螺力矩的影响,从而改善了飞机悬停和过渡飞行时的稳定性,提高了飞机的机动性能。
国内外对双转子系统动力特性的研究日趋成熟。但在可参考的研究资料中,反向旋转双转子的参考文献并不多。在国内,冯国全和张连祥等人对反向旋转双转子发动机稳态不平衡响应进行了研究[1]。罗贵火、胡绚等人对反向旋转双转子系统的动力特性进行了计算和试验[2-3]。在国外,印度学者K.Gupta等人应用传递矩阵法计算了反向旋转双转子系统的不平衡响应,并对该系统的临界转速、振型和不平衡响应进行了实验研究[4]。法国学者 M.Lalanne和 G.Ferraris在《Rotordynamics Prediction in Engineering》一书中应用Rayleigh-Ritz方法对反向旋转双转子系统的动力特性进行了分析[5]。本文围绕一个简易的双转子模型,运用有限元方法计算该双转子系统反向旋转时的临界转速和主振型,并分析了双转子系统的中介轴承刚度和转速比对该转子系统临界转速特性和振型的影响。
1 结构模型与参数
反向旋转双转子模型如图1所示。该双转子内外转子上各有两个盘,整个系统共有四个支承,中介轴承3的内圈与内转子联接,外圈与外转子联接。相对于单转子系统来说,由于中介轴承的影响,双转子系统的振动变得更为复杂。
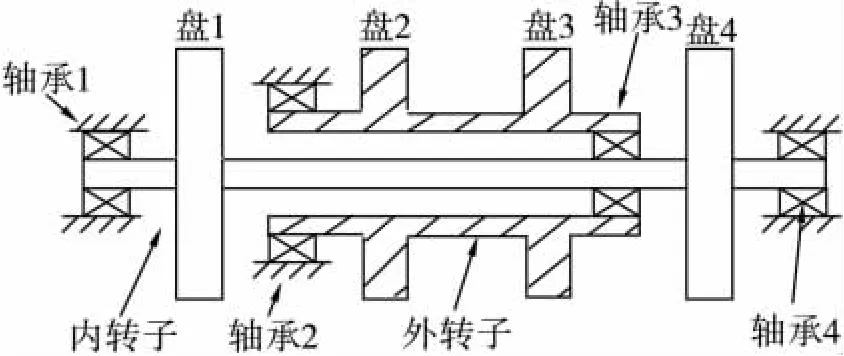
图1 双转子结构简图
该双转子系统的结构参数如表1所示。假设轴承是各项同性的,且不记阻尼的影响,各个轴承的刚度参数如表2所示。本文主要研究该双转子模型的临界转速特性和振型特点,以及中介轴承刚度和转速比对临界转速和振型的影响。
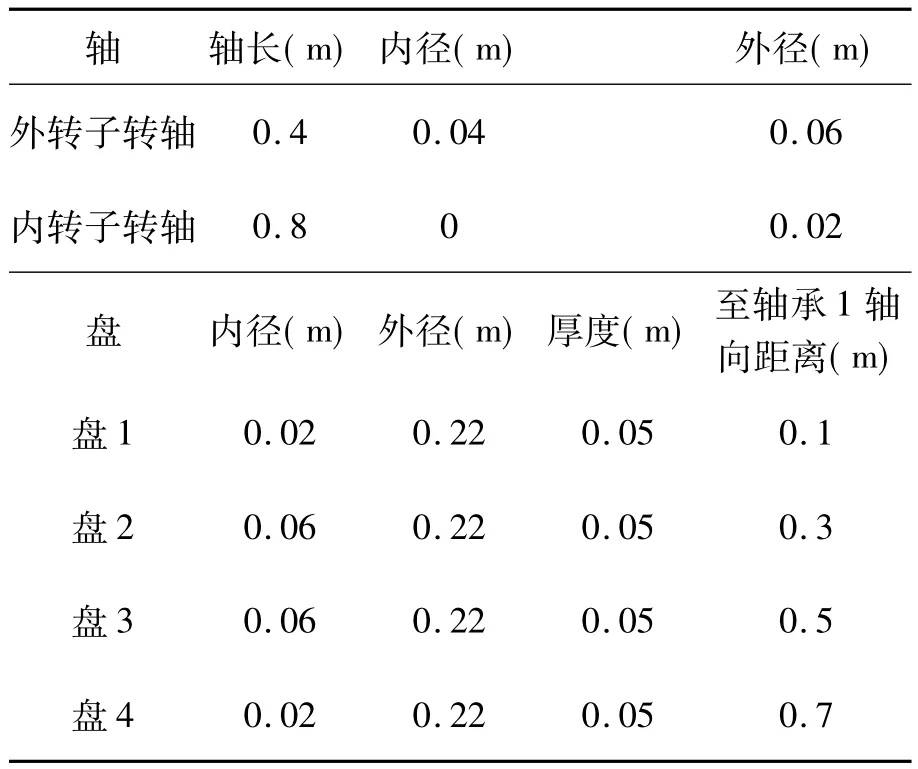
表1 双转子系统结构参数
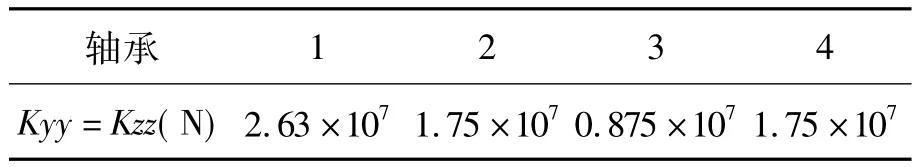
表2 轴承刚度
2 有限元建模
2.1 模型的简化
采用ANSYS对图1所示双转子系统模型建立有限元模型,基于以下简化[6-7]:
(1)转轴作为梁处理,考虑转动惯量、陀螺力矩、连续质量和剪切变形的影响;
(2)盘作为集中质量,考虑其质量和转动惯量;
(3)支承和轴承作为弹簧阻尼单元处理。
2.2 单元类型选择
为适应不同分析的需要,确定单元类型是很重要的。ANSYS提供了近200多种不同的单元类型,从普通的的线单元、面单元、实体单元到特殊的接触单元、间隙单元和表明应力单元等。在建模过程中,选择了3种单元 BEAM188、COMBI214和MASS21来分别构成双转子系统中的轴段、轴承和轮盘,从而组成了整个双转子系统。3种单元的简介如下:
(1)BEAM188是三维线性(2节点)或者二次梁单元。该单元基于铁木辛哥梁结构理论,并考虑了剪切变形的影响。该单元在转动时可以考虑陀螺效应的影响。每个节点有6个自由度;节点坐标系的 x、y、z方向的平动和绕 x、y、z轴的转动。前处理时,BEAM188的材料特性和截面尺寸可用实常数的形式来定义。
(2)COMBI214是一个二维的轴承单元,共有两个节点,每个节点有两个自由度,不考虑弯曲和扭转。在二维应用中,COMBI214既有纵向又有交叉方向的功能。该单元有4个刚度系数和4个阻尼系数。单元模型如图2所示。假设轴承是各项同性的,Kyy=Kzz,Kyz=Kzy=0,且不记阻尼的影响。
(3)MASS21是一个具有6自由度的点单元,这6个自由度分别为沿x、y、z方向的平移和绕x、y、z方向的转动。该单元可以把盘作为集中质量处理,可以分别在6个自由度的方向上分配不同的质量和转动惯量。双转子系统中的盘可简化为如表3所示的具有集中质量和转动惯量的点单元。
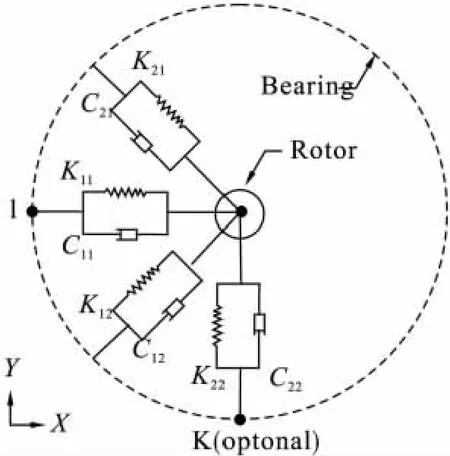
图2 COMBI214单元模型
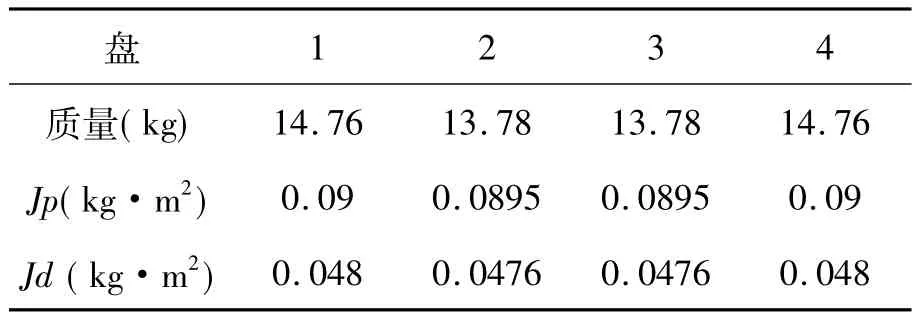
表3 盘的质量和转动惯量
2.3 网格独立性检验
为保证计算的精度,需要对梁单元划分的网格的独立性进行检验。用有限元法进行计算时,一般来说,网格越密,计算精度越高。在考虑计算机时和保证计算精度的前提下,将双转子系统内轴的轴向分为8段,轴截面周向均分为32份,截面径向分为2份,外轴的轴向分为4段,轴截面周向均分为32份,轴截面径向为1份。网格布局如图3所示,整个转子系统有限元模型关于轴向完全对称。通过多次计算分析,该种网格布局可以满足计算精度的要求,可以获得与网格无关的解。本文所计算的双转子有限元模型(图4)均为此种网格布局。
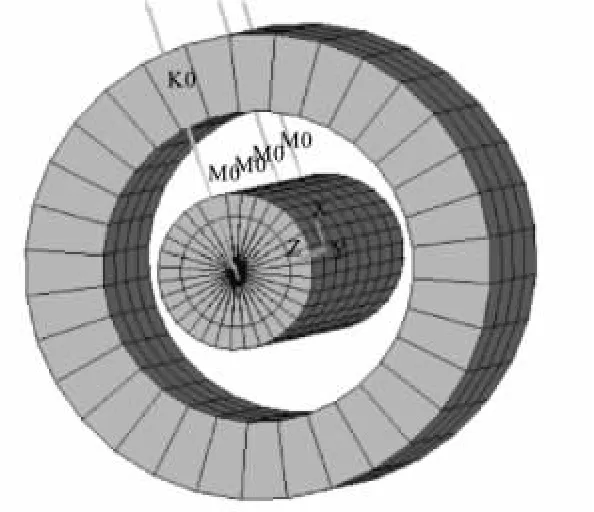
图3 转子系统网格布局
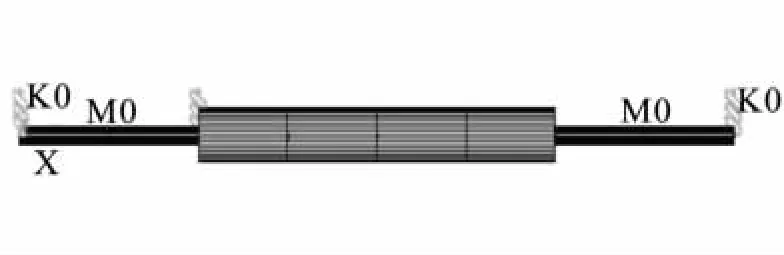
图4 双转子系统的有限元模型
2.3 动力学方程
动力学分析是有限元法的一个重要的应用范围,系统的动力学方程可以由节点的平衡条件来导出。节点上的作用力主要分为两类[8]:作用于节点上的外载荷与相关单元对该节点的作用力。汇集所有的节点方程,便得到结构的动力平衡方程,用矩阵符号表示为:
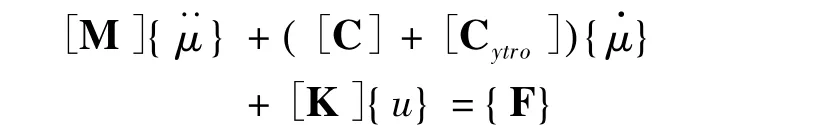
式中:M为结构的整体质量矩阵;C为结构的整体阻尼矩阵;Cgyro为陀螺矩阵;K为结构的整体刚度矩阵;F为结构的整体载荷向量;μμ&、μ&&、分别为结构的节点位移、节点速度、节点加速度向量。该式是用有限元法求解结构动力问题的基本方程,简称为动力方程。计算一个转子系统的临界转速,就是计算该动力方程的特征值。本文不考虑轴承阻尼的影响,由于结构阻尼对结构的固有频率和振型影响很小,所以在计算系统的固有频率和振型时阻尼可以忽略不计。
3 动力学特性分析
3.1 临界转速与振型分析
双转子系统同向和反向旋转时,陀螺力矩对两者的动力学特性将产生不同的影响。一般在转子部件中,主要是考虑轮盘的陀螺力矩对转子系统动力特性的影响。当轮盘作正进动时,陀螺力矩将使转轴的当量刚度增加,因而提高了转子的临界转速;当轮盘作反进动时,陀螺力矩将使转轴的当量刚度减小,因而降低了转子的临界转速。对于同向旋转的双转子系统,在不平衡力的驱动下,两个转子一般作正进动,内转子或外转子为主激励的临界转速比不考虑陀螺力矩时增加了。对于反向旋转的双转子系统,以内转子为主激励的转子的转动方向与进动方向一致,转速等于进动转速,内转子作协调正进动,从而提高了系统的临界转速,而外转子的转向与进动方向相反,且转速不等于进动转速,外转子作非协调反进动,从而降低了系统的临界转速,因此陀螺力矩对反向旋转双转子系统的影响要小于同向旋转的双转子系统。由于同向旋转和反向旋转双转子运动方式的不同,两者的临界转速和振型存在着一定的差异。
图1所示的双转子系统中,外转子与内转子的转速比为1.5,轴和盘的材料属性为:杨氏模量E=2.1 ×1011Pa,密度 ρ=783 kg/m3,泊松比 μ =0.3。根据表1、2和3中的数据分别编制该双转子系统同向旋转和反向旋转临界转速的有限元计算程序,得到该双转子系统两种不同运动方式下的前3阶临界转速如表4所示,对应的振型如图5(图左半部分为同向旋转的振型,右半部分为反向旋转的振型)所示。
由表4可以看出:
(1)该双转子系统同向旋转和反向旋转时,以外转子为主激励的前三阶临界转速小于以内转子为主激励的前三阶临界转速;
(2)该双转子系统反向旋转时的前三阶临界转速要小于同向旋转时的前三阶临界转速;
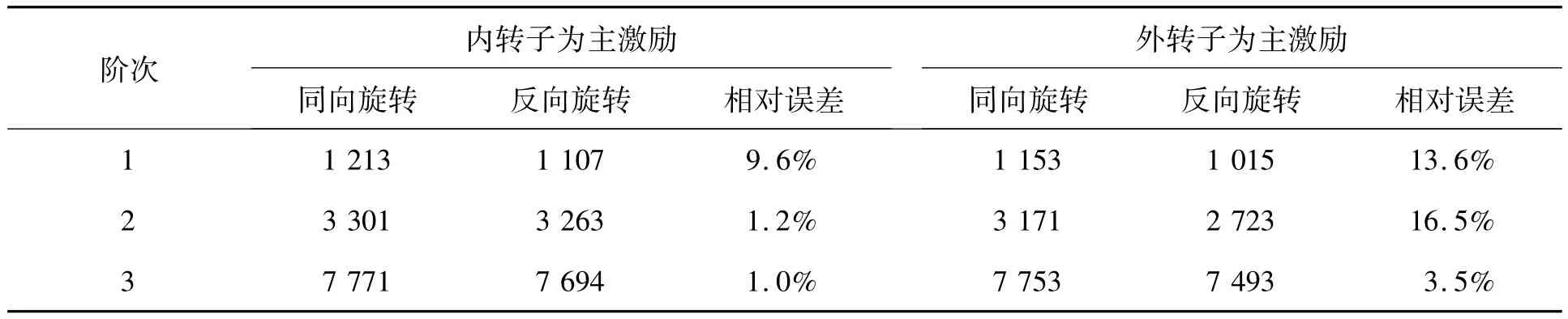
表4 双转子系统前3阶临界转速(rpm)
(3)由于陀螺力矩的影响,双转子系统同向和反向旋转时,以外转子为主激励时的临界转速的相对误差要大于以内转子为主激励时的临界转速的相对误差;
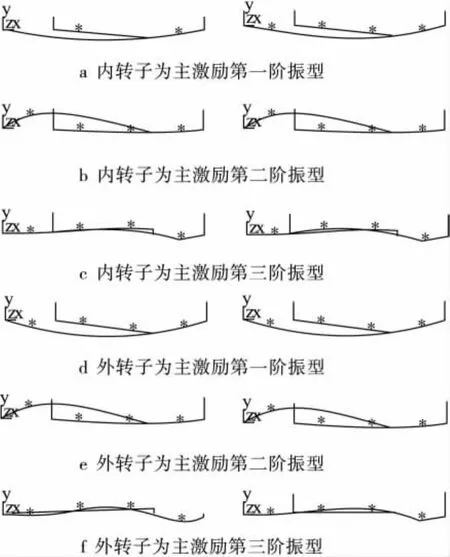
图5 同向旋转和反向旋转的前三阶振型对比
(4)相对于同向旋转的双转子,反向旋转双转子以外转子为主激励时对临界转速的影响要大于以内转子为主激励时的影响。
由图5可以看出:
(1)同向旋转和反向旋转的前两阶振型的几乎保持一致,第三阶振型才有明显差别。这是因为陀螺力矩随转速的变化而变化,在低转速时,陀螺力矩相对较小,因此对系统振型的影响较小,而在高转速时,陀螺力矩较大,对系统振型的影响较大;
(2)同向旋转和反向旋转时,由于陀螺力矩的影响,以内转子为主激励的第三阶振型中,外转子的振型变化较大,而以外转子为主激励的第三阶振型中,内转子的变化较大。
3.2 中介轴承刚度的影响
理论和实验都已证明支承刚度对转子系统的临界转速有较大的影响。本节主要用有限元方法研究反向旋转双转子系统中介轴承刚度对其临界转速的影响,即只改变表2中轴承3的刚度系数来研究系统的临界转速特性,外转子与内转子的转速比为1.5。当中介轴承3的刚度变化时,对应的反向旋转双转子系统的临界转速如表5所示。图6和图7给出了中介轴承在2×106~6×107N/m范围变化时,对应的由内转子和外转子为主激励的前三阶临界转速。
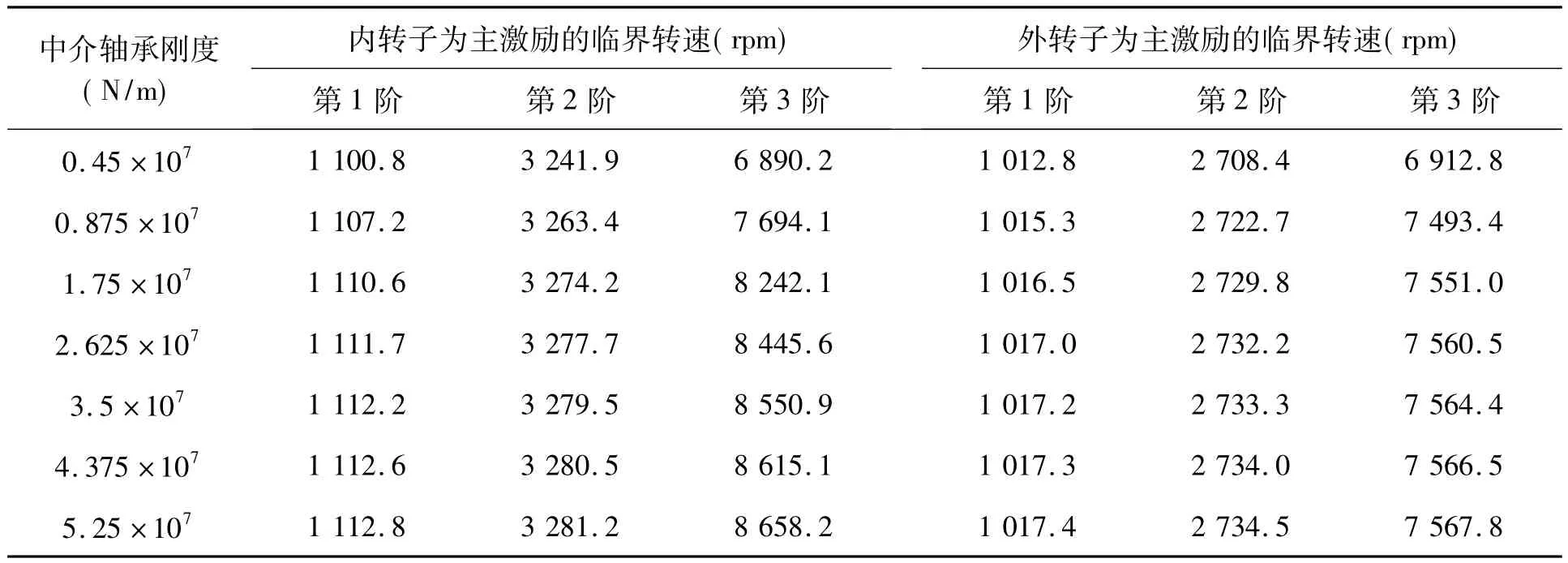
表5 中介轴承刚度对临界转速的影响
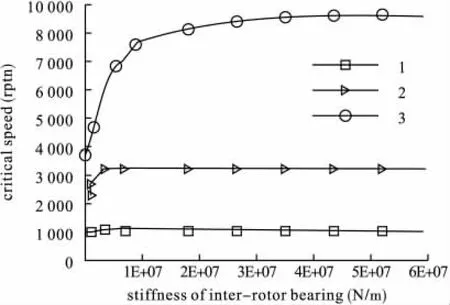
图6 中介轴承对内转子为主激励的临界转速的影响
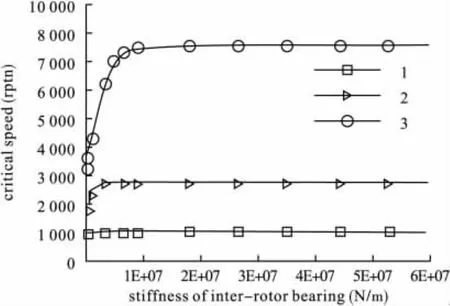
图7 中介轴承对外转子为主激励的临界转速的影响
由表5、图6和图7可以看出,中介轴承刚度的变化对该转子系统的第二和第三阶临界转速影响较大,对第一阶的临界转速影响较小。转子系统的临界转速随着中介轴承刚度的增加而增加,增加的幅度越来越小,最后临界转速趋于一个定值,因为这时中介轴承可被视为刚性的,再增加其刚度对临界转速的影响将很小。
3.3 转速比的影响
本文中取外转子与内转子的转速比为定值来研究反向旋转双转子系统临界转速特性。在使用有限元方法计算时,通过只改变双转子系统的转速比来计算前三阶临界转速,计算结果如表6所示。由于篇幅原因,只取转速比为0.6和1.5时,对应的第三阶临界转速时的振型如图7(图左半部分为同向旋转的振型,右半部分为反向旋转的振型)所示。
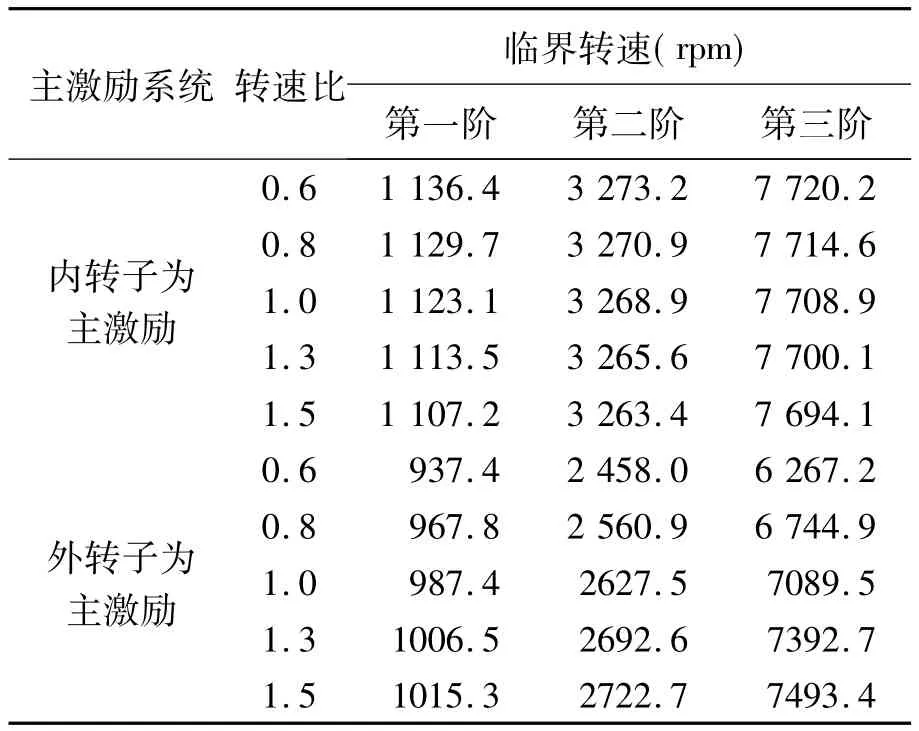
表6 转速比对临界转速的影响
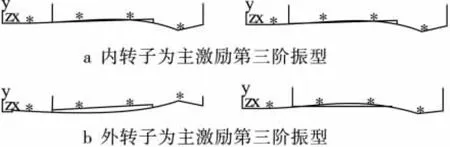
图8 转速比为0.6和1.5时第三阶振型
由表6和图8可以看出:
(1)双转子系统反向旋转时,随着转速比的增大,以内转子为主激励的临界转速逐渐减小,以外转子为主激励的临界转速逐渐增大;
(2)转速比对内转子为主激励的临界转速的影响要小于外转子为主激励的临界转速的影响;
(3)转速比的变化对双转子系统的主振型有影响,且内转子为主激励时外转子振型变化较大,外转子为主激励时内转子振型变化较大。
4 结论
本文用有限元方法计算了一个反向旋转双转子系统的动力学特性,另外还计算和分析了中介轴承刚度和转速比对临界转速的影响。通过对计算结果的对比分析,可得到如下重要结论:
(1)由于陀螺力矩的影响,双转子系统同向和反向旋转时,以外转子为主激励的临界转速的相对误差要大于以内转子为主激励的临界转速的相对误差;
(2)同向旋转和反向旋转时,由于陀螺力矩的影响,以内转子为主激励的第三阶振型中,外转子的振型变化较大,而以外转子为主激励的第三阶振型中,内转子的变化较大;
(3)中介轴承的刚度变化对高阶临界转速的影响大于对低阶临界转速的影响,对内转子为主激励的临界转速的影响要大于对外转子为主激励的临界转速的影响;
(4)转速比对内转子为主激励的临界转速的影响要小于外转子为主激励的临界转速的影响。
[1]冯国全,张连祥,伊峰.反向旋转的双转子发动机稳态不平衡响应分析[C].中国振动工程学会第五届转子动力学学术会议,1999.
[2]罗贵火.反向旋转双转子系统振动特性分析与试验研究[D].南京:南京航空航天大学,1999.
[3]胡绚,罗贵火,高德平.反向旋转双转子系统动力特性分析[J].现代机械,2007(4):45- 49.
[4]Gupta,K.Unbalance response of a dual rotor system:theory and experiment[J].Journal of Vibration and Acoustics,1993,115(4):427 -435.
[5]Lalanne M,Ferraris G.Rotordynamics Prediction in Engineering[M].England:Wiley,1989.
[6]张谦,曹磊.基于ANSYS的临界转速计算[J].振动工程学报,2004,17(21):234 -237.
[7]张利民,王克明,吴志广.利用ANSYS进行转子临界转速计算[J].沈阳航空工业学院学报,2010,27(5):34-37
[8]韩清凯,于涛,王德友,等.故障转子系统的非线性振动分析与诊断方法[M].北京:科学出版社,2010.
