一种基于FPGA的二维DCT和IDCT的新算法

赵 滨，黄大庆

（南京航空航天大学 无人机研究院，江苏 南京210016）

一种基于FPGA的二维DCT和IDCT的新算法

赵 滨，黄大庆

（南京航空航天大学 无人机研究院，江苏 南京210016）

提出了一种新的二维DCT和IDCT的FPGA实现结构，采用行列快速算法将二维算法分解为两个一维算法实现，其中每个一维算法采用并行的流水线结构，每一个时钟处理8个数据，大大提高电路的数据吞吐率和运算速度。通过Modelsim仿真工具对该设计进行仿真，证明该算法的功能的正确性，进行一次8*8的分块二维DCT变换仅仅需要16个时钟，满足图像以及视频实时性的要求。

二维DCT算法；二维IDCT算法；流水线；FPGA

近年来，数字形式的图像信息的应用需求不断增加，对数字图像处理的要求也不断提高。随着信号处理技术的不断发展，使得数字图像处理技术与系统在各个行业与领域中得到广泛而充分的应用。DCT广泛应用于图像压缩，语音压缩和数字水印等技术中，JPEG，MPEG和H.264等标准都采用了DCT技术作为压缩编码的主要方案[1]。JPEG算法中8*8图像块的二位DCT变换如果直接进行运算，运算量巨大，传统的MCU和DSP难以满足实时处理的需要，而FPGA的并行处理能力，特别适合于数字信号处理领域的应用，过去的几年，就DCT算法的快速VLSI实现已经做了很多的工作，在硬件实现时资源利用率和互联复杂性等方面有着优异的性能[2]。笔者在此基础上提出了一种并行流水线结构，充分利用FPGA片上丰富的嵌入式算法器和可编程逻辑资源，构建了一个每一个时钟处理8个数据的结构单元，大大提高了数据的吞吐量。

1 算法描述

1.1 DCT算法

1.1.1 一维DCT算法

设{x（n）}为N点实序列集合，n=0 ，1 ，……N-1，其一维DCT 定义[3]为：

其中：

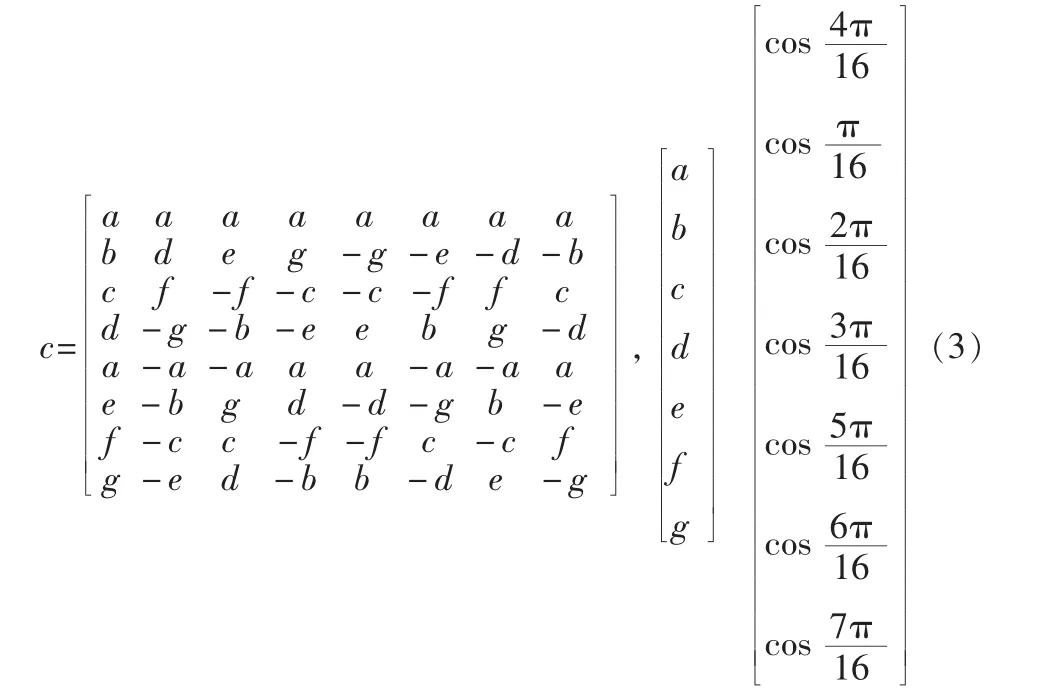
利用c的对称性，由式（2）可得：

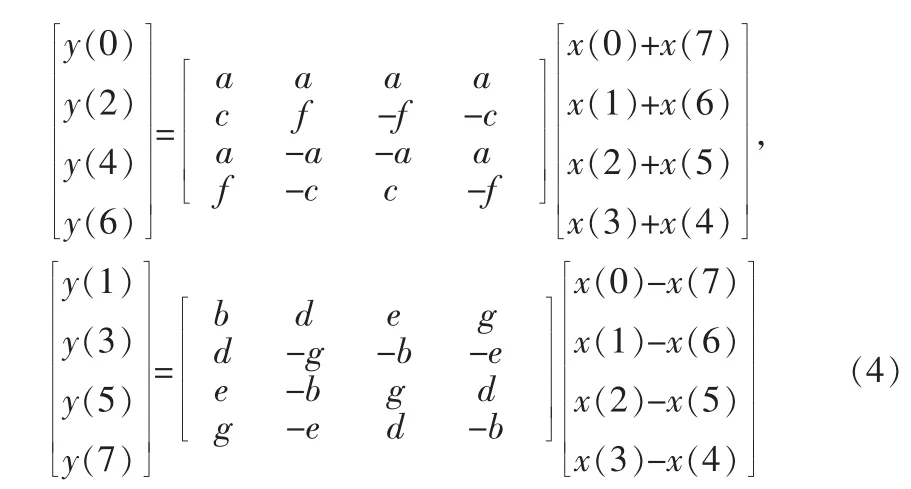
所以，可得：利用三角公式：cos（a+b）=cosa·cosb-sina·sinb 得到：

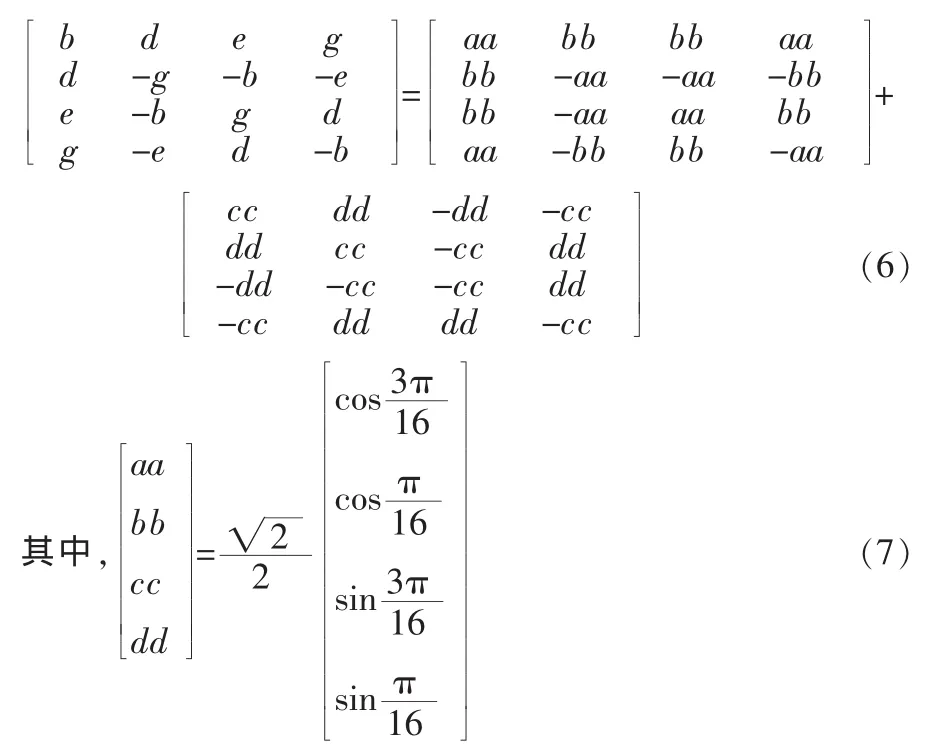
从而有：

从而可以得到计算一维DCT变换的流水线示意图，如图1所示。

1.1.2 二维DCT算法

对于一个大小为N×N的像素快来说，假设x（i，j）为输入的像素点阵数据，其二维DCT变换公式如下：

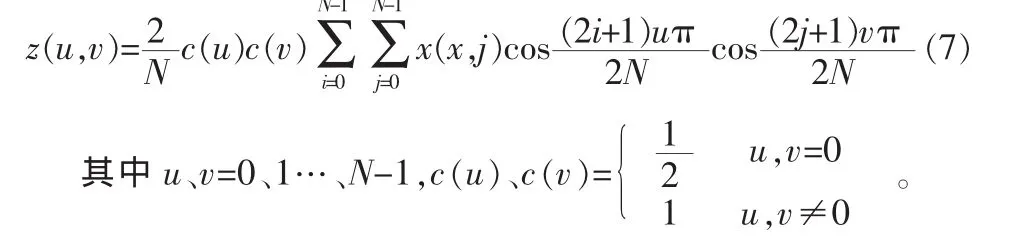
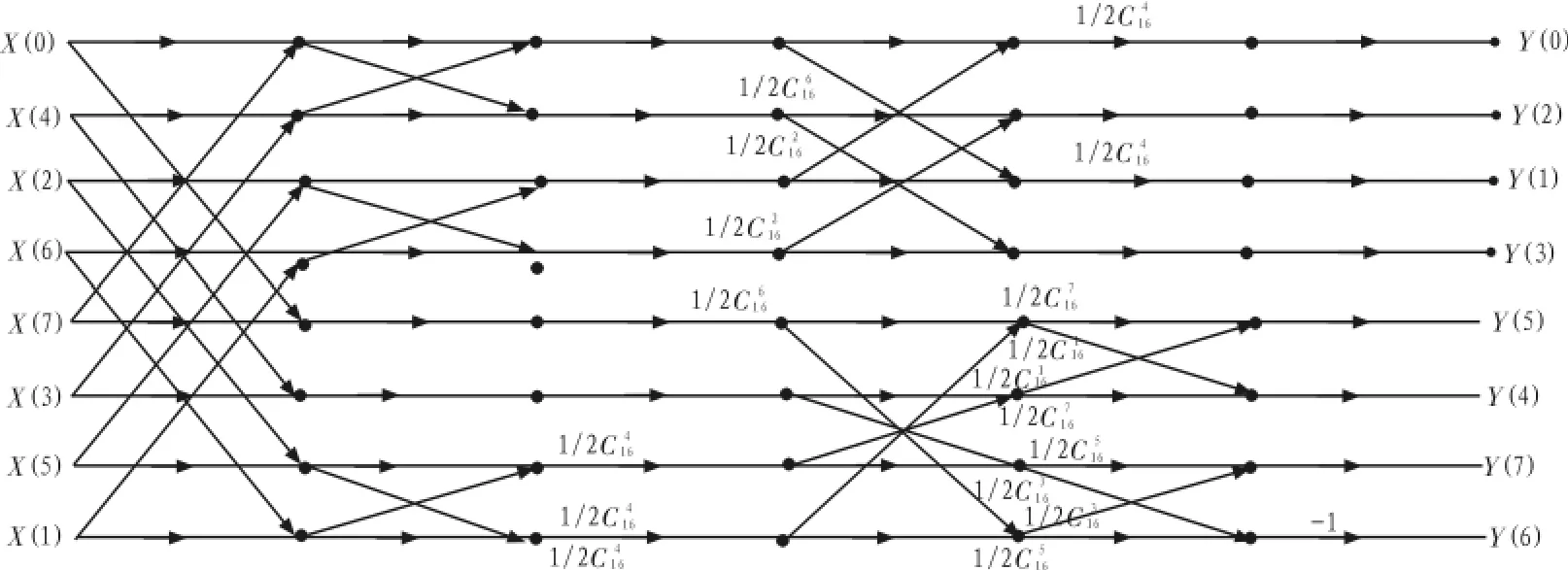
图1 一维DCT的流水线结构Fig.1 The pipeline framework of the 1-dimensional DCT

上式很容易写成矩阵形式：z=cxcT，其中c为带余弦基本函数的变换系数矩阵，更进一步，可以将二维DCT变换分解:z=cy，y=xcT，这样，在进行二维DCT变换时，可以应用一维DCT变换来计算，即先沿x的行进行一维DCT计算获得y，再对y的装置行进行一维DCT变换[5]。

1.2 IDCT 算法

1.2.1 一维IDCT算法

N点的DCT（IDCT）反变换的计算公式如下：

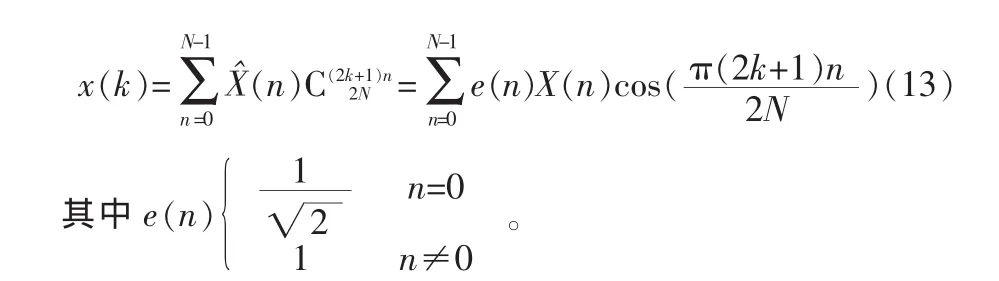
根据n分解为奇数和偶数项，得到：

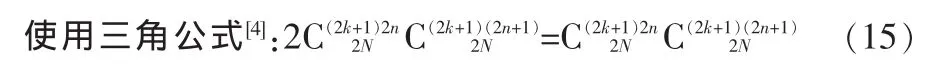
分解可得，一维逆DCT的流水线结构如图2所示。

这里采用与DCT变换相似的方法，将逆DCT变换设计为8个时钟的流水线操作，每个时钟输出一个数据。以方便与DCT变换模块交互。

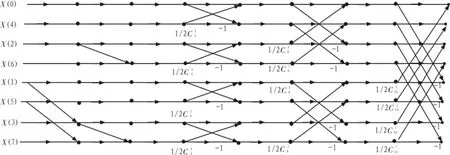
图2 一维逆DCT的流水线结构Fig.2 Pipeline framework of the 1-dimensional iDCT

1.2.2 二维IDCT算法

与二维DCT变换一样，相应的逆DCT变换也可以采用分布的方式实现，即先对图像块的每一行进行一维DCT变换，实行行变换，然后对经过行变换的图像块的每一列再进行一维逆DCT变换，从而实现二维逆DCT变换[6]。

2 功能仿真与验证

整个电路使用Verilog语言进行描述，在Quartus2中综合后，在Modelsim工具中进行仿真，我们输入以下2个8×8的矩阵块 A，B：

通过2-DCT模块的仿真结果如图3所示，与MATLAB结果比较，验证了模块功能的正确性，同时由一维DCT模块可以看出，由于使用了流水线结构，这样可以实现每个时钟处理8个数据，大大提高了变换的速度，可以使用在需要实时进行DCT的应用中，而进行一个二维8×8的DCT只需要16个时钟，满足图像处理实时性的要求。

将上述输出结果输入的二维IDCT变换模块，得到的输出结果如图4所示，与原始输入比较，证明了该模块的正确性：

3 结论

图3 二维DCT变换模块的仿真结果Fig.3 Simulational result of the 2-dimensional DCT module

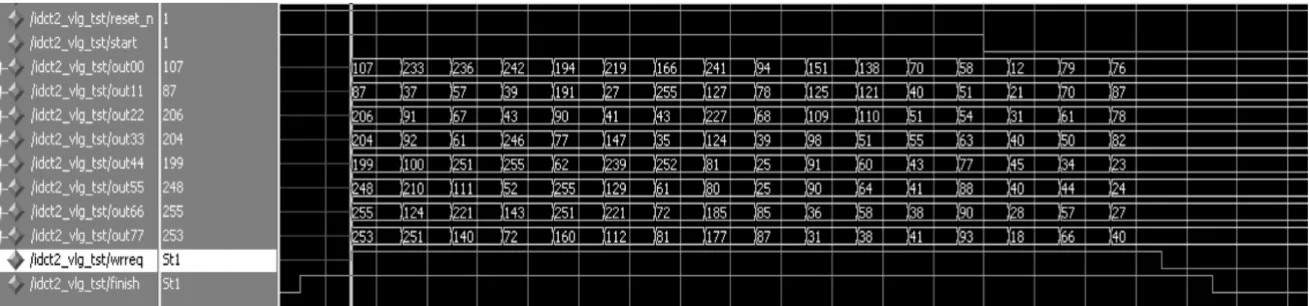
图4 二维DCT反变换的仿真结果Fig.4 Simulational result of the 2-dimensional IDCT module

提出了基于FPGA的二维DCT变换和IDCT变换实现结构，并行的流水线算法使得该二维DCT和IDCT变换具有较高的数据吞吐率和处理速度，完成一次一维DCT和IDCT变换的计算仅仅消耗一个时钟，同时进行一次二维DCT和IDCT仅仅需要16个时钟，与其他设计相比，大大提高了运算的速度，满足图像、视频处理中实时性的要求。可以用于实时性要求较高的视频和图像处理系统中。

[1]Conzalez R C，Woods R E.数字图像处理[M].阮秋琦，阮宇智，译.北京:电子工业出版社，2003.

[2]陈普跃，赵新璧，陈斌.二维DCT快速算法及FPGA实现[J].电子质量，2008（2）:5-7.

CHEN Pu-Yue， ZHAO Xin-bi， CHEN Bin.Fast 2-D discrete cosine transform algorithm and its implementation based on FPGA[J].Electronics Quality，2008（2）:5-7

[3]钟文荣，陈建发.二维DCT算法的高速芯片设计[J].厦门大学学报，2005（2）:198-201.

ZHONG Wen-rong，CHEN Jian-fa.FPGA implementation of high throughput 2D-DCT[J].Journal of Xiamen University，2005（2）:198-201.

[4]田耘，徐文泼，张延伟.数字信号处理的FPGA实现[M].北京：电子工业出版社，2008.

[5]郭爱平.DCT算法优化及其在数字水印中的应用[D].兰州：兰州大学，2010.

[6]李芳.基于H.264/AVC的视频编码技术研究与FPGA实现[D].重庆:重庆大学，2008.

A new algorithm of two dimesion DCT and IDCT based on FPGA

ZHAO Bin，HUANG Da-qing
（Research Institute of Unmanned Aircraft，Nanjing Universty of Aeronautics and Astronautics，Nanjing210016，China）

A new algorithm of two dimentional cosine transform （DCT） and inverse discrete cosine transform （IDCT）based on FPGA is presented.The architecture uses a row-column decompostion to break the 2-D algorithm into two 1-D algorithm.The 1-D algorithm uses the parallel pipling architecture and one clock can process 8 datas that makes the circuit work with high data throughput and speed.Through the design tools of Modelsim and Quartus，the circuit is simulated and verified.The result shows the corroctness of the design and it can finish a two dimesional DCT or IDCT in 16 clocks，so it can meet the requirement of real_time in video processing.

2-D DCT；2-D IDCT；pipeline；FPGA

TP391

A

1674－6236（2011）24-0126-04

2011-10-14 稿件编号：201110059

赵 滨（1982—），男，吉林吉林人，硕士。研究方向：遥控遥测。