基于力学分析的主轴轴系结构优化设计

王海涛 李初晔

(北京航空制造工程研究所，北京 100024)

主轴是数控机床的核心和关键部件，因而主轴轴系结构的优劣，在很大程度上决定了数控机床整体的加工精度、运行稳定性和生产效率。对于精密机床，主轴轴系结构的合理性显得更为突出，当今一些重要的生产加工领域，精密加工已成为发展趋势和重要内容之一。力学是机械设计的基础，以力学分析作为切入点，对主轴轴系进行优化和完善，不失为一种有效的处理方式和手段。

1 问题的来源

本文以现有的ZJT－310型和对其改进中的ZJT－320A型精密镗床主轴轴系结构为基础，根据主轴运行过程中的受力情况，分别转换成力学简图，并介入力学分析和计算，得出相应的关键数据，进行比较，以对主轴轴系结构进行优化设计。

ZJT系列镗床属于精密加工设备，因为该机床主要用来镗削加工高精度圆柱孔，主轴支承采用液体静压轴承，因此，主轴本身的变形、主轴和电动机转子自重等的影响，都会导致主轴偏离回转中心和自身变形的产生。由于所加工孔的圆柱度不大于0.001 5 mm，表面粗糙度为Ra0.4 μm，而且主轴回转精度的设计要求为0.002 mm，机床整体的技术参数和精度指标较高，所以，上述变形、自重等不可控因素的轻微波动，都会影响机床主轴的回转精度和加工精度。

ZJT－310型精密镗床已成功应用于生产近6年，中间也进行了多次小的改进，主要围绕着改善主轴驱动结构和降低温升进行，动力传动从最初的V带传动改为多楔带传动，最后改成“准电主轴”型，直接将电动机转子安装在主轴上，有效地降低了径向载荷和温升对轴系精度的影响，使机床的加工精度产生了一次飞跃。

但是，随着客户对加工件精度要求的逐步提高，镗床的加工精度只有随之跟上，才能抓住竞争日益激烈的市场。通过充分分析论证发现，结合力学理论，通过实施结构优化，主轴回转精度还有较大的提升空间。

2 ZJT－310型镗床轴系结构分析

2.1 轴系结构简述

该型号机床主轴轴系结构采用前、后静压轴承支承，主轴驱动通过将三相交流电动机转子直联在主轴后端实现(图1)，镗削不同材料和孔径尺寸的工件所需主轴转速通过变频器来调节。

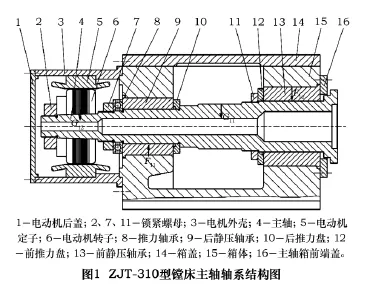
主轴支承所使用的静压轴承采用小孔节流方式，利用外部液压站供给压力油，进入静压轴承周边的油腔，以形成承载油膜，由液压油的静压力平衡外载荷，使主轴浮在静压轴承中间位置，确保在一定的允许转速和负载范围内，主轴和静压轴承之间处于液体摩擦状态，可获得极低的摩擦因数。

2.2 力学分析和计算

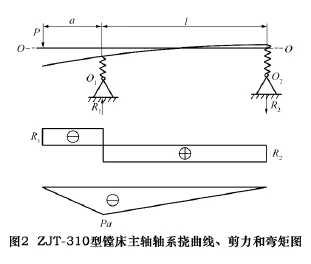
如图1所示，G11表示主轴自重，G12表示电动机转子自重，F11表示后静压轴承支承力，F12表示前静压轴承支承反力。根据图中主轴的受力状态，可转化成轴系的挠曲线、剪力和弯矩图，如图2所示。其中:O－O线代表主轴轴心线，O1、O2表示前、后静压轴承支承点，R1=F11，R2=F12，P=G12，经计算可知:支承力R1=(1+a/l)P，R2=(a/l)P，弯矩Mmax=Pa。

为简化轴系变形量的计算，忽略主轴的微小弯曲变形，保留电动机转子自重引起的主轴整体偏转量，将图2中的挠曲线图等效成图3所示的形式。其中，Δ为转子中心偏移量，Δ1为后静压轴承偏移量，Δ2为前静压轴承偏移量，θ为主轴偏转角度，需要求出主轴总偏移量，即Δ总=Δ+Δ2，以此与改进后的方案结果进行相应比较，进而进行下一步的轴系结构优化工作。

设计时设定前、后静压轴承的支承刚度系数为K=K1=K2，则有:Δ1=R1/K，Δ2=R2/K，tanθ=(Δ1+Δ2)/l，于是有 θ=tan－1［(Δ1+Δ2)/l］。

所以Δ总=Δ+Δ2=(l+a)tanθ，将θ值代入，可得:

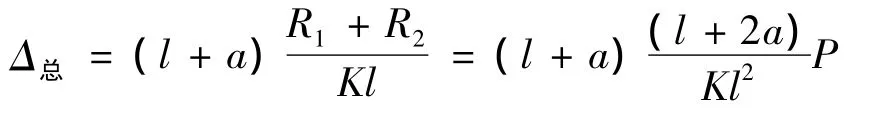
代入各个已知参数的实际数值后，通过计算可以得到主轴的总偏移量Δ总=0.025 8 mm。

3 ZJT－320A型镗床轴系结构方案分析

3.1 轴系结构方案简述

该方案是为了进一步优化主轴轴系的受力结构而实施的。原来的ZJT－310型镗床电动机转子后置结构，导致主轴偏移的产生，降低了主轴运转的稳定性和运转精度。现在方案的改进，在不考虑整个轴系水平偏移量的前提下(这个水平偏移量对主轴各项精度的影响甚微)，主要存在电动机转子和主轴自身重量使主轴产生的变形。

3.2 力学分析和计算

如图4所示，G21表示主轴自重，G22表示电动机转子自重，F21表示后静压轴承支承力，F22表示前静压轴承支承力。在方案设计时，通过计算，将电动机转子重心和主轴重心重合，便于分析和比较方案的合理性。

同样，根据主轴的受力及状态，可转化成轴系的挠曲线、剪力和弯矩图，如图5所示。其中:O－O线代表主轴中心线，O1、O2表示前、后静压轴承支承点，经计算可知:R1=F21，R2=F22，P=G21+G22，假设G21和G22引起主轴的最大变形量(也即挠度)为vmax，经计算可知:

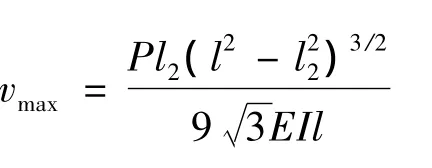
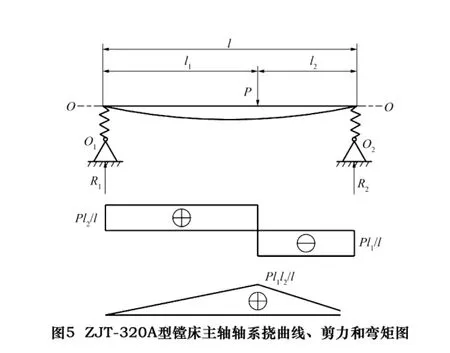
其中:I为主轴的截面惯性矩，若主轴外径为D，内孔直径为d，则I=(D4－d4)π/64。代入各个已知参数的实际数值后，通过计算最后可以得出主轴的最大变形量vmax=0.001 96 mm。

计算结果显示vmax≪Δ总，从理论角度证明了改进方案的合理性。下面再通过样机的生产、制造和加工，做进一步证明和检验。

4 比较验证

ZJT－320A型镗床轴系结构方案经过理论计算确认可行后，进行了样机的生产制造，并在调试和试镗削后，将该镗床应用到了生产线上，经过近3个月的生产检验，测量数据表明该机床加工精度和加工效率有了显著提高，主轴振动也得到了明显改善。对型号镗床按检验规程进行测量，与ZJT－310型镗床的原始测量值进行了比较，主要技术参数均值如表1所示。

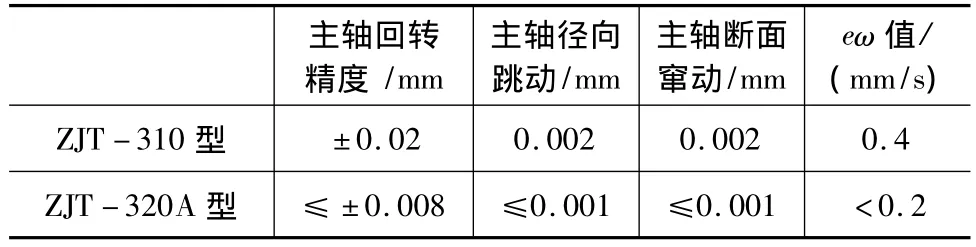
表1 两种型号镗床主要技术参数比较

通过测量数据可以知道，ZJT－320A型镗床主轴轴系各项主要精度指标明显得到提高和改善，这从“硬件”上保证了工件的加工精度。

随机从生产现场抽检了100只工件进行测量，尺寸精度全部符合图纸的设计要求。与ZJT－310型镗床相比较，通过计算，加工件各项测量均值如表2所示。

表2 两种型号镗床加工精度测量均值比较

数据表明，ZJT－320A型镗床所加工工件的参数指标和精度得到了明显提高，相对ZJT－310型镗床，又向前迈进了一大步。

5 结语

通过以上优化工作的具体实施，结合技术工作的实际，得出以下几点启示:

(1)理论分析与生产实践相结合，使设计开发过程既有基础理论作指导，又有生产结果做验证，整个工作流程形成一个良好的“闭环控制”，使设计或改进的成果得以发展和进步。

(2)机床结构的优化有多种方法，可以根据具体的问题，进行分析论证，确定采取某种或某几种组合来进行处理。例如，本文只从力学分析的层面进行计算论证，实际操作上也可以再辅以有限元分析进行验证，最后进行方案的实施。

(3)机床结构的优化、改进和完善是一个循序渐进的过程，在生产实践和科研设计之间建立一个反馈平台，适时进行沟通交流，一旦时机成熟，立即实施。

(4)对于优化处理较为复杂的机械结构，可从基础点出发，由点及面，找寻出最为可行的方式，可省时省力，取得事半功倍的效果。

(5)机床结构的优化是为了提高机床的加工精度，进而提高企业的市场竞争力。要结合加工件的精度对机床进行优化，并不是加工精度越高越好，满足精度需求的前提下，也要考虑成本因素。

(6)机床关键部件的优化建立在机床整体状态良好的基础上，没有机床整体性能作保障，局部的结构优化只能是空中楼阁。

［1］徐灏.机械设计手册:新版［M］.北京:机械工业出版社，2004.

［2］苟文选.材料力学(Ⅰ)［M］.高等院校教材.北京:科学出版社，2005.

［3］王启义.中国机械设计大典［M］.南昌:江西科学技术出版社，2002.

［4］张根保，王时龙，徐宗俊.先进制造技术［M］.重庆:重庆大学出版社，1996.

［5］王爱玲，白恩远，等.现代数控机床［M］.北京:国防工业出版社，2003.

［6］覃文洁，左正兴，等.机床整机的动态特性分析［J］.机械设计，2000(10).