吉布斯自由能的多功能性质探讨

张颖

(陕西师范大学化学与材料科学学院 陕西西安 710062)

按照国际纯粹与应用化学联合会(IUPAC)的定义，吉布斯能量(Gibbs energy)或吉布斯函数(Gibbs function)是焓减去热力学温度和熵的乘积，即G=H-TS，常称为自由能(free energy)或自由焓(free enthalpy)。与其他热力学函数一样，吉布斯自由能也具有状态函数的属性，即其变化值ΔG只决定于系统的始态和终态，而与变化的途径无关。Gibbs自由能具有广泛的功能特性，如在等温、等压条件下可作为过程与方向的判据，还具有狭义化学势、最大非膨胀功和狭义表面自由能等功能。

1 Gibbs自由能判据[1-2]

在等温、等压条件下，根据热力学第一定律和第二定律的联合表达式：

-δWf≤-d(U+pV-TS)或-δWf≤-d(H-TS)

可以得到-δWf≤-dG或dG≤δWf。该式的物理意义为：在等温、等压条件下，一个封闭系统所能做的最大非膨胀功等于其Gibbs自由能的减少。换句话说，在等温、等压的可逆过程中，Gibbs自由能的减少等于系统对外所做的最大非膨胀功。因此，在实际变化过程中，可通过Gibbs自由能的降低值来度量某一封闭系统能够做有用功(即非膨胀功)的最大能力，可以表示为 dG=δWf,max或ΔG=Wf,max。

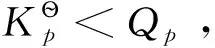
若系统在等温、等压且不做非膨胀功的条件下，其变化值可以表示为-ΔG≥0或ΔG≤0，即自发变化总是朝着Gibbs自由能减少的方向进行，直至平衡为止；系统不可能发生ΔG>0的变化。Gibbs自由能的变化值可作为等温、等压且不做非膨胀功条件下自发变化方向的判据。由于大多数反应都是在等温、等压条件下进行，与其他判据相比，Gibbs自由能判据更为常用。

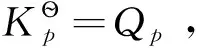
2 狭义化学势[1-2]

在多组分系统中，每一组分的行为与各组分单独存在时不一样，这是由于不同种类的分子间的相互作用与同类分子间的相互作用不同。因此，在处理敞开系统或组成发生变化的封闭系统的热力学关系时，Gibbs和Lewis引入了化学势的概念。化学势是宏观物理量，它可将各组分之间的所有影响因素都包含在内。

对于一个多组分系统，其热力学基本方程式可表示为：

dG=Vdp-SdT+μAdnA+μBdnB+…

恒定温度和压力条件时，dG=μAdnA+μBdnB+…

因此，Gibbs自由能具有的狭义化学势的特性为计算ΔG提供了一条途径。

dG=μAdnA+μBdnB=-μAdξ+μBdξ=(μB-μA)dξ

由上式可以看出，在化学反应系统中，ΔrG可以看作是反应物和生成物之间化学势的差值。在恒定温度和压力条件时，可以利用反应物和生成物化学势数值的大小来判断反应的自发性，即当μA>μB时，ΔrG<0，即A→B正向反应自发进行；当μB>μA时，ΔrG>0，B→A逆向反应自发进行；μA=μB时，ΔrG=0，反应达平衡。

3 最大非膨胀功[1-3]

在等温、等压条件下，当系统发生变化时，其Gibbs自由能的减少等于对外所作的最大非膨胀功，可表示为(dG)T,p=δWf,max或(ΔrG)T,p=Wf,max。通过dG=μAdnA+μBdnB+…关系式，也可以表示为Wf,max=μAdnA+μBdnB+…。此式表明，某一系统组成的变化会产生非膨胀功。例如，在化学电池中，化学反应分别在两个不同位置(两个电极)发生，电功则是随着体系中的物质由反应物变为产物而产生的。

对某一实际系统而言，若非膨胀功只有电功时，系统Gibbs自由能的减少即等于对外所作的最大电功，表示为 (ΔrG)T,p=Wf,max=-nEF。当(ΔrG)T,p<0时，电池电动势E为正值，表明电池反应在热力学上是自发的，即发生自发反应的电池才能做有用的电功；当(ΔrG)T,p>0时，E为负值，表明电池反应是非自发反应。

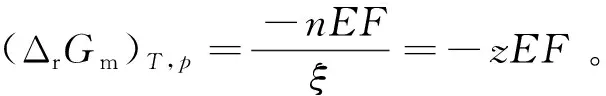
4 狭义表面自由能[2-4]

在表面物理化学的研究中，在指定各相应变量不变的情况下，每增加单位表面积时，系统热力学能或Gibbs自由能等热力学函数的增加值称为广义表面自由能，可表示为：

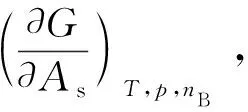
基于Gibbs自由能所具有的狭义表面自由能的性质，可以对很多实际系统进行分析。例如，在胶体分散系统中，其聚结过程是热力学的自发过程，即ΔG<0，当表面张力γ为恒值时，ΔAs<0，即要缩小表面，只有通过聚结或聚并作用[4]。在实际系统的研究中，为获得稳定的胶体体系，常需要加入分散稳定剂(如高分子、表面活性剂等)，在胶体表面形成表面结构层，以达到缩小表面的作用；另外，加大空间位阻，可以避免胶体粒子之间的聚结或聚并作用的发生，达到稳定胶体的目的。

选用高分子物质作为胶体系统的分散稳定剂时，当浓度和相对分子质量合适时，吸附在胶体颗粒表面的高分子物质可以降低胶体的表面能，有效避免颗粒聚集过程的发生，使胶体颗粒稳定。当高分子物质浓度较低时，不能将每个胶体颗粒包住，反而起到架桥作用，使颗粒间产生吸引作用，最终发生絮凝。因此，在很多实际体系中，如污水处理，高分子絮凝剂在加入量少时容易发生絮凝，而加入量多时可以起到保护胶体的作用。另外，利用分散制备法获得固体分散体系时，常加入表面活性剂来稳定胶体颗粒。表面活性剂的加入，不仅能降低表面张力，而且在胶体颗粒表面形成溶剂化膜或双层膜，达到降低胶体颗粒表面能的作用，使得胶体颗粒更稳定。

5 Gibbs自由能计算实例

与其他热力学状态函数一样，ΔG数值常通过设计可逆过程进行计算，但由于Gibbs自由能特有的化学势特性，在有些条件下也可通过化学势的计算来获得ΔG数值。另外，在电化学体系中，由于某些电池中进行的电极反应不易达到平衡，因而不能通过电化学实验的方法直接测定电动势E的准确值。可通过热力学状态函数计算ΔrGm，再根据热力学与电化学之间的桥梁公式ΔrGm=-zEF得到电池电动势E。

解法1：在等温、等压条件下，不可逆相变过程的ΔG常可通过设计可逆过程的方法进行计算。在已知条件充分的情况下，同一题目可设计出不同的可逆过程。

思路1：从初态出发经过3步可逆过程到达终态，即设计如图1所示的可逆过程。

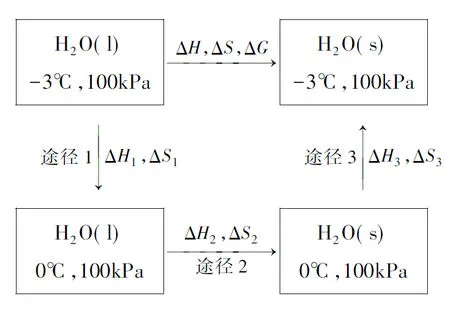
图1可逆过程(途径1+途径2+途径3)

设T1=270K，T2=273K，分别求出3步途径中的ΔH和ΔS，即可以通过ΔG=ΔH-TΔS关系式求得ΔG。

ΔH=ΔH1+ΔH2+ΔH3=-5745J，ΔS=-21.04J·K-1，ΔG=(-5745+270×21.04)J=-63.9J

思路2：假设从初态出发,经5步可逆过程到达终态，即设计图2所示的可逆过程。

图2可逆过程(途径1+途径2+途径3+途径4+途径5)

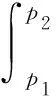
所以有：

解法2：不借助可逆途径，利用吉布斯自由能的化学势属性进行计算，即分别通过初始态和终态的化学势来计算实际变化过程的ΔG，ΔG=μ(H2O,s)-μ(H2O,l)。

图3状态变化过程

设:

p1=489Pa(-3℃时水的蒸气压)，p2=475Pa(-3℃时冰的蒸气压)

其中，

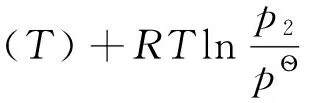
(1)

(2)

由于μӨ(T)均为-3℃时的气相纯物质对应的标准态，其值相等，故(1)式减去(2)式，可得：

解法3：通过吉布斯-亥姆霍兹公式进行计算。

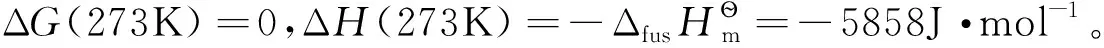
根据吉布斯-亥姆霍兹公式：

(3)

设T1=273K，T2=270K，假定由273K到270K温度范围内ΔH为常数，积分式(3)，得：

代入数据，计算得ΔG(270K)=-64.4J

例2[6]：已知298K时，反应2H2O(g)2H2(g)+O2(g)的平衡常数为9.7×10-81，这时H2O(l)的饱和蒸气压为3200Pa，试求298K时下述电池的电动势E：

Pt|H2O(pӨ)|H2SO4(0.01mol·kg-1)|O2(pӨ)|Pt

解：反应2H2O(g)2H2(g)+O2(g)在298 K时的平衡常数是根据高温下的数据间接计算得到的。电池中氧电极上的电极反应不易达到平衡，因此不能通过电化学方法测定电动势E的精确值，但可通过热力学方法计算E。

首先写出所求电池对应的电池反应如下：

该电池是一个氢氧燃料电池，若求出该电池反应的ΔrGm，即可得到电池电动势E。

通过设计可逆过程，将所求电池反应与题中给出了平衡常数的反应相结合，利用热力学状态函数的性质，可计算出电池反应的ΔrGm。

设计如图4所示的可逆过程。

图4可逆过程(途径1+途径2+途径3)

途径1对应的反应即题中给出的水蒸气分解反应的逆反应。

ΔrGm,1=RTlnKӨ=RTln(9.7×10-81)=-456.46kJ·mol-1

途径2是气体的简单状态变化。

途径3是饱和蒸气压下的气-液两相平衡，ΔrGm,3=0。

由此可得电池反应的ΔrGm和E。

ΔrGm=ΔrGm,1+ΔrGm,2+ΔrGm,3=(-456.46-17.06+0)kJ·mol-1=-473.52kJ·mol-1

[1] 傅献彩,沈文霞,姚天扬,等.物理化学(上册).第5版.北京:高等教育出版社,2006

[2] Atkins P,Paula J.Atkins′ Physical Chemistry.第7版.影印版.北京:高等教育出版社,2006

[3] 傅献彩,沈文霞,姚天扬,等.物理化学(下册).第5版.北京:高等教育出版社,2006

[4] 江龙.胶体化学概论.北京:科学出版社,2002

[5] 范崇正,杭瑚,蒋淮渭.物理化学-概念辨析解题方法.合肥:中国科学技术大学出版社,1999

[6] 孙德坤,沈文霞,姚天扬,等.物理化学学习指导.北京:高等教育出版社,2008