基于最短时间的公交乘车路径查询模型

夏 伯 男, 吴 雪 莹, 姚 春 龙

( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )

0 引 言

一个公交查询系统的核心问题就是解决出行者的出行路线问题,通过出行者提供的起始点和目的地,从换乘次数、距离、时间等多个方面分析途径的站点,最后给出符合出行者要求的最佳路线。据在北京市做的一个公交乘客出行心理调查统计结果,在换乘次数、出行距离、出行耗时3个因素中,有56.8 %的乘客在选择出行路径时首先考虑的是换乘最少,其次考虑时间最短。因此,目前提出的公交查询模型和算法通常将换乘次数作为首要因素。首要考虑换乘次数的乘车路径算法已经有很多,比如最小换乘算法[1]及其改进算法[2]、分层规划算法[3]、蚂蚁算法[4]等。最小换乘算法基本思想是：先判断是否有直达线路,如果没有再判断是否有1次换乘到达路线,如果没有再继续增大换乘次数继续判断直至存在到达路线[5]。在上述情况中如果存在不止一种的选择方案,则再考虑乘车距离,选择路程最短的乘车方案[6-7]。

上述算法各自有各自的优点,但缺陷也很明显。如当考虑时间权值时,这些算法没有考虑到换乘时换站点所花费的时间和在站点等待的时间,这样算出的时间最短路径不一定是最快的路线。本研究讨论的模型把换乘和等待的时间都以特定的方式赋予不同权值后参与到时间权值小的路径查询中,这样得出的路径更直观、具体、准确。

1 系统模型

系统是基于一种带权有向图的公交查询系统。当人们查询的是一个城市内部公交路线的时候,用带权有向图给出符合用户要求的最佳路径及推荐路径。

1.1 公交线路

城市内部错综复杂的公交线路组合在一起形成了一个完善的城市公交网,而每条公交线路都包括了数个公交站点,排除起始站和终点站,每个站点都有自己的前续站点和后续站点,根据这个特点去描述公交线路的结构。

对于任一公交模型E,记S为所有站点的集合,W为相邻站点i和j的关系的集合。用站点编号来表示站点：

下行方向：1—2—3—4—5—6,

上行方向：6—7—4—3—2—1,

则有：

S={S1,S2,S3,S4,S5,S6,S7},

W={w1,2,w2,3,w3,4,w4,5,w5,6,w6,7,w7,4,w4,3,w3,2,w2,1}。

实际上,线路模型E与图1所示的有向图相对应。从图中可以明显看到,线路的上行和下行方向所经过的站点不完全相同。

图1 线路E对应的有向图

1.2 公交查询模型

公交查询模型,就是根据出行者给出的起始站点、目的站点和出行者选择的优先条件选出最优乘车路线。出行者不同,考虑的优先条件往往不尽相同,因此,公交查询模型的设计要充分考虑到这些需求。下面给出一种通过查询图来定义一个乘车方案的查询模型。

设E是一个这种新的公交网络中所有公交线路的集合。对于指定的出发站点Si和目的站点Sj,有i和j的查询图,记作Eij,它是一个有向带权图。其中：

(1)设顶点集合为S={v|v=(s,l),它是一个二元组,满足对于任意线路l∈E且站点s∈S}∪{Sa,Sb}。Sa和Sb分别为出发顶点和目的顶点,用于表示出发站点和目的站点这两个特殊顶点。在本模型中,出发站点和目的站点的时间权值设为0。

(2)设弧的集合为W={WN,WM,WL,WS}。WL,WS分别是同线弧、换乘弧的集合。

WN={〈u,v〉|〈u,v〉是出发弧。即u,v∈S；u为始发站}；

WM={〈u,v〉|〈u,v〉是结束弧。即u,v∈S；u为终点站}；

WL={〈u,v〉|〈u,v〉是同线弧。即u,v∈S；u,v为相邻站点且u≠v}；

WS={〈u,v〉|〈u,v〉是换乘弧。即u,v∈S；u,v为相同站点且u≠v}。

由此可见,查询图中有四类弧：出发弧、结束弧、同线弧、换乘弧。同线弧是连接同一线路上站点相邻的顶点间弧,换乘弧为连接线路不同但站点相同(出发和目的站点除外)的顶点的弧,这些顶点实际上描述了换乘站信息。

图2描述了一个简单的城市公交带权查询图。可以很清晰地看出从出发的站点1到目的站点12之间经过的所有站点和分支。其中,相连的同线弧看作一条乘车路线,换乘弧相连的两个站点看作换乘站点。

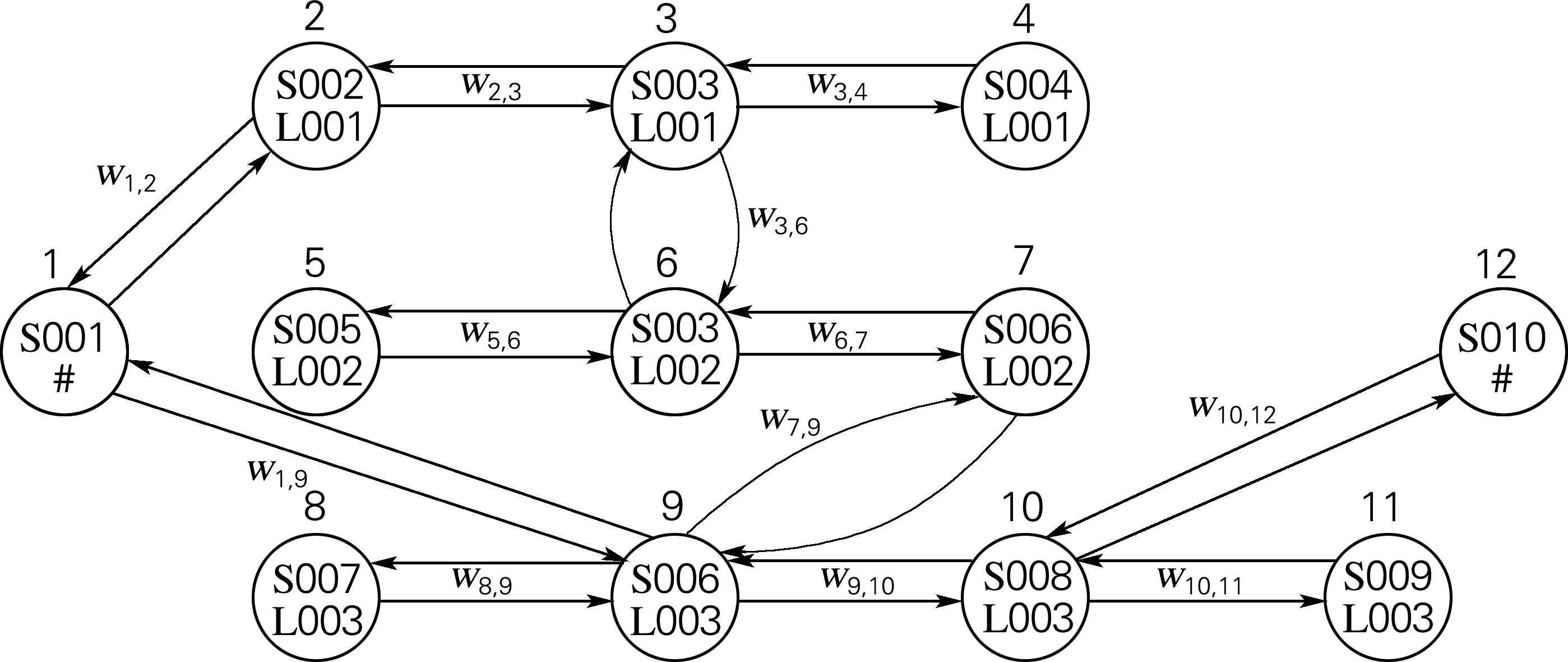
图2 公交换乘查询图

2 查询图的权值设定策略

大部分用户在选择乘坐公交路线的时候,都以换乘次数最少或者路径最短和时间最短等为最优选择条件。在此基础上再考虑乘车舒适度等其他因素。这些在各大中城市中是很常见的乘车需求,这就需要公交查询系统能够提供不同的优先条件选择,如路程最短、时间最短、换乘最少等。以时间最短为优先条件,通过查询图的权值设定策略来实现上述三级优先查询的目标。以图2为例：

wij记做换乘弧和同线弧,如果wij为出发弧或结束弧时,wij=0。

wij为换乘弧,则查询路径经过wij时,需要考虑两部分的时间权值,一部分是,如果两路公交车的换乘站在不同位置,要考虑两站之间的步行时间的权值,记作cij；另一部分是到达目的站点后,在站台等待公交车的时间作为权值,记作dij；则在公式中wij=cij+dij。在公交换乘地铁的站点,由于地铁站上下行需要经过楼梯,所以cij≠0；但是,公交站换乘站点在相同情况下,cij可能为0。站台等待时间dij为到达站点后,到上车时间的等待时间权值,由于是随机情况,可能的权值在0至发车间隔的时间,为了方便计算,一般把等待时间权值估算为发车时间的1/2,但是在不同时间段,公交车的发车间隔可能不同。

wij为同线弧,同线弧是某条公交线路经过2个站点之间所花费的时间。如图2所示,一条公交线路经过5,6,7,12四个站点,则该公交线路的同线弧时间权值分别为w5,6,w6,7,w7,12。在实际过程中,需要测量在不塞车状态下,公交车经过站点的时间作为同线弧的时间权值。为了计算方便,一般可以使用全程运行时间/(站点数目-1)的结果,估算出同线弧的时间权值。

如图2所示,公交系统包含3条公交线路。经过的站点分别为{1,2,3,4},{5,6,7,12},{8,9,10,11}。

出发弧：w1,2,w1,9；

结束弧：w7,12,w10,12；

换乘弧：w3,6,w6,3,w7,9,w9,7；

同线弧：w1,2,w2,3,w3,4,w5,6,w6,7,w7,12,w8,9,w9,10,w10,11。

通过上面的集合可以得出公交系统E起于节点1结束于终点12的通路是：

P1={1,2,3,6,7,12}；

P2={1,9,7,12}；

P3={1,9,10,12}。

(1)记通路的时间权值为Qi,以P1为例,Q1=w1,2+w2,3+w3,6+w6,7+w7,12,其中w1,2是出发弧,w7,12是结束弧；w3,6是换乘弧。

所以,可以求得3条通路的时间权值分别为

Q1=w1,2+w2,3+w3,6+w6,7+w7,12；

Q2=w1,9+w9,7+w7,12；

Q3=w1,9+w9,10+w10,12。

一条通路的时间权值之和越少,代表这条通路花费的时间越短。因此,Qmin就是需要的那条通路,即最优解。

(2)实际中,对于一个复杂的城市公交系统,如果查询所有情况,会使得到结果的时间过长,而且大部分是无用的。如果查询到了一条线路,在没有到达终点之前,时间的权值已经大于已经获得结果的线路,那么这条查询路径就舍掉。使用算法实现时,当有多条线路同时能够到达某一目标点,则只保留时间权值最小的路径,这样在有N个站点的城市公交系统中,程序中保留的站点最多不超过N-2个。

(3)当Qmin有多个解的时候(包括中间的站点),要舍掉部分多余的结果。本系统在基于时间权值相同的情况下考虑换乘最少,然后考虑公交线路的始点站。

求解出的最优解Qmin满足路程时间权值最短、最少换乘、优先始发站的三级优先查询要求的查询。在实际应用中,由于城市的不同,导致站点和公交线路的复杂程度区别很大。在效率要求较高的系统中,如果到达某一站点的时间权值相同时有多个解,酌情减少在中间站点中保存的线路数目,能够显著提高搜索效率。

3 模型实现

为了验证和测试提出的模型,以大连市内的公交网为背景,用C#语言实现了一个简单的城市公交查询系统。大连有部分公交线路的上行和下行方向所经过的站点不相同,不同车型还有其自身的线路,例如：快速公交、有轨电车、轻轨等。各种公交线路共计140多条,形成了由市区线路、旅游观光线路、支线公交、郊区线路构成的城市公交主干体系。

首先取得公交线路的同线弧长度W,假设该公交线路驶完全程的时间为D,公交站点个数为a,则该线路的同线弧时间权值为W=D/(a-1)。

换乘弧的时间权值记作WS,包括两部分时间：两站之间的步行时间的权值C和在站台等待公交车的时间D。C的时间权值需要GIS数据采集。为了叙述简便,将需要走路换乘的站点的C设置为TC,站台等待时间假设为公交发车频率的1/2,将公交车的发车频率记为TD。要注意一点就是不同时间区间,同一班公交车的发车频率可能不同。y站点的换乘弧WS=TC+TD/2。

为了说明方便,将始发站和终点站的换乘弧权值WN,WM设置为0。

在实现中,以从[西南路]到[兴工街]的线路查询为例,叙述时间查询最短模型实现方法。如图3所示,在最佳乘车方案中,公交线路经过7个车站。从始点到终点依次为：[西南路]-[净水厂]-[台山村]-[南沙街]-[汉阳街]-[解放广场]-[兴工街],程序中使用的是蚂蚁拓扑算法计算时间权值的方法。

在始点[西南路]站,始点站WN=0,经过该站的公交车有32路和32路加车,与该站点相连的同线弧站点分别为：[净水厂][西南桥],通过公式W=D/(a-1)得到WL=5。在查询站点结果列表中,保存这2个站点的时间权值和路径信息,然后以权值最小的站点开始,遍历站点。先遍历列表中的[净水厂]站点,经过[净水厂]站点的公交车有10路、32路和32路加车。在换乘站点,10路与32路车在同一位置,记C=0,10路公交车发车间隔为6 min,由公式得出D=3。

[西南路]遍历到[解放广场]站,此时从[解放广场]遍历到周围站点时,要到达[兴工街]站,需要换乘。在[解放广场]换乘时,需要加上换乘弧的权值,202路站点和32路站点在不同位置,设202路的步行时间权值C=5,等待时间权值为D=3,则WL=C+D=8。

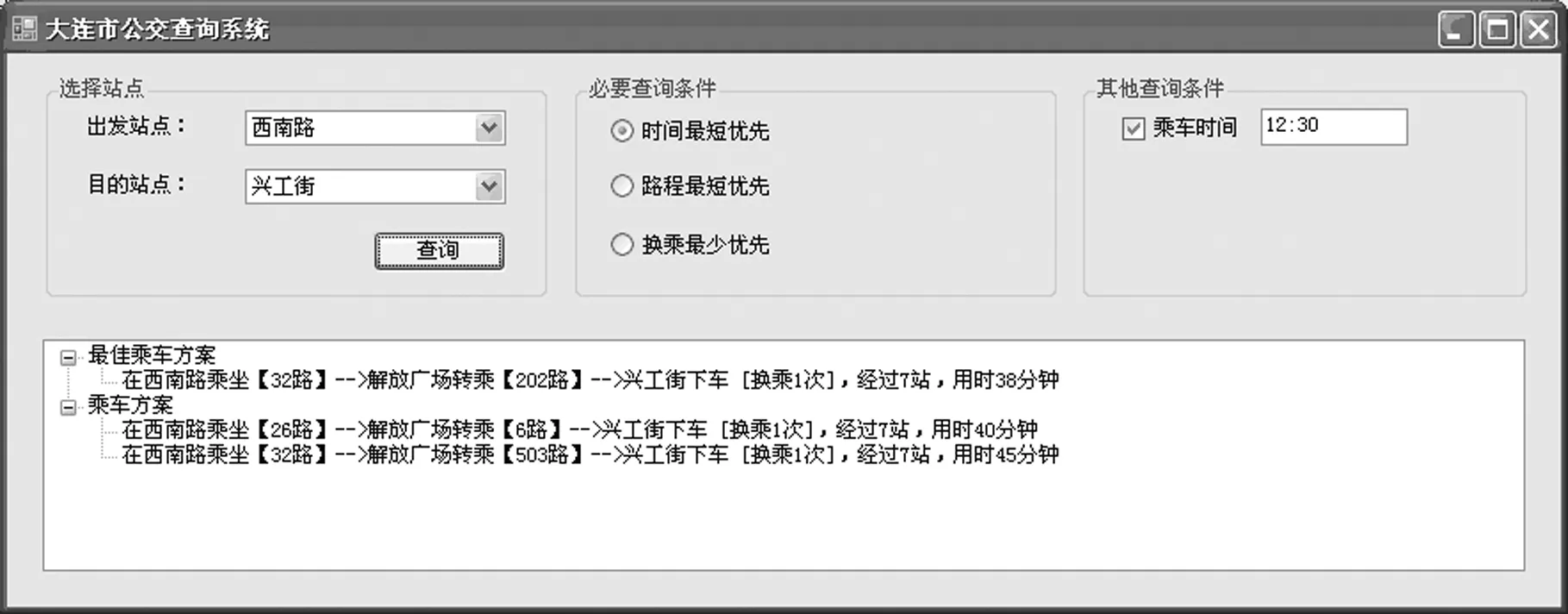
图3 时间最短查询

如图4所示,由于优先条件为路程最短,那么求最优解的过程就基本和以时间权值为优先条件的求解过程相同。不同的是需要求出每条线路在通路中的经过多少同线弧的数量和各自路程权值的乘积而不是时间权值,另外不同的是路程最短需要考虑换乘时从一个线路的A站,走到另一个线路的A站的路程,而不考虑时间,等待时间也不考虑。

图4 路程最短查询

4 结束语

分析了公交查询模型的最优算法,在比较现有算法研究的基础上,提出了一种基于时间最短的层次搜索查询算法。虽然理论研究和算法实现取得了一些研究成果,但是在具体的过程中存在一些不足,有几个问题要进一步改进和研究：第一,没有考虑到公交线路上,不同时间的路况的情况,比如在上下班高峰期,公交车的行车速度会减慢,这样就会导致时间权值的增加,但地铁、快速公交等线路,不受此影响。第二,在获得换乘线路等待时间的权值时,是以发车间隔的1/2作为权值计算的,这只是一个估算,不能精确地得到等待时间的权值。

[1] 陆忠,钱翔东,张登荣. 基于最短路径查询的城市公交网络拓扑建模研究[J]. 遥感信息, 2002(1):11-14,46.

[2] 王玉琨,吴锋. 嵌入式GIS最短路径分析中Dijkstra算法的改进[J]. 计算机工程与应用, 2008, 44(28):128-129.

[3] 陈洪仁,冯树民. 分层限制的公交线网优化模型[J]. 哈尔滨建筑大学学报, 2001, 34(5):113-115.

[4] 高为民. 基于蚂蚁算法的公交网络最短路径问题研究[J]. 交通与计算机, 2007, 25(1):94-95,105.

[5] 傅冬绵. 交通系统中最少换乘算法及其实现[J]. 华侨大学学报:自然科学版, 2001, 22(4):348-350.

[6] 翁敏,毋河海,杜清运,等. 基于公交网络模型的最优出行路径选择的研究[J]. 武汉大学学报:信息科学版, 2004, 29(6):500-503.

[7] 苏莹,王英杰,余卓渊. 一种建立公交网络的最短路径改进算法[J]. 地球信息科学, 2005, 7(2):99-104.