基于MUSIC算法的双平面阵列天线DOA估计

王 洪 海, 李 鹏, 王 智 森

( 大连工业大学 信息科学与工程学院, 辽宁 大连 116034 )

0 引 言

DOA(Direction of Angel)估计是自适应天线的核心技术之一,只有得到准确的DOA估计值,自适应阵列天线才能将主波束对准用户信号到达方向,旁瓣或零陷对准干扰信号的到达方向,有助于在上行和下行处理中的波束形成,以实现智能天线降低系统干扰,增加系统容量的功能。

当前讨论较为充分的阵列形式有均匀直线阵列ULA(Uniform Linear Array)[1],L型阵列[2],十字形阵列和均匀圆阵UCA(Uniform Circle Array)[3-4]等。ULA阵结构简单,易于分析,可以在给定阵元数的情况下实现阵列垂直方向上具有的最大物理孔径,但不足是在阵元连线方向(或接近此方向)上,阵列口径很小,且DOA估计只能是一维的,不能对信号源方位进行准确估计。L形阵列孔径明显在其阵列两臂延长线方向上变小。十字形阵列当信源接近两臂延长线方向时会存在着方向角模糊问题；当信噪比较低时,这种情况尤为明显。文献[8]给出了角度模糊问题的解决方法,但都存在不足之处。本研究采用两个相互垂直放置的双平面阵列天线,并基于MUSIC算法对三维空间到来角的三个参数分拆后分别进行DOA估计,最后通过提出的参数配对方法对参数进行配对,从而得到三维空间到来角,较好地解决了角度模糊问题。

1 阵列模型的建立

图1是双平面阵列示意图。一个平面阵列在xoy面垂直放置,另一阵列在xoz面水平放置,x轴上不放置天线阵元。阵元A、B与原点的距离均取为半波长,每个平面阵列的阵元数分别为N×N,阵元为线性阵元,各阵元等间距分布。

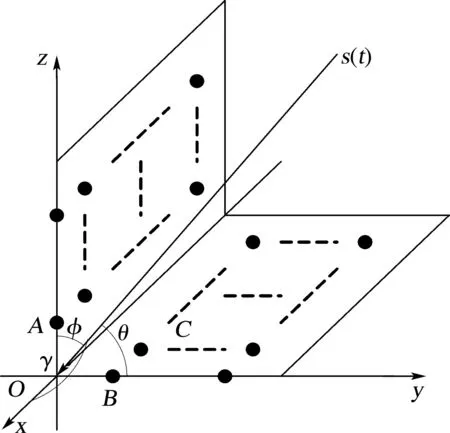
图1 双平面阵列示意图

假设K个信号源位于远场区,以平面波入射；信号源与y轴所成的角设为θk,与z轴所成的角设为φk(k=1,2,3,…,K),与x轴的夹角设为γk。这三个角分别在0°～180°取值。虽然这三个角是相关的,但三维空间里的任意一个空间三维角都可以用这三个角来表示；反过来任意这样的三个角都对应着一个三维空间角。也就是说它们相互之间是一一对应的。因此,这样的取法是合理的。

由立体几何知识可以得到

cos2θk+cos2φk+cos2γk=1

(1)

则阵元B相对于阵元O的相位差可以表示为dxcosθk/λ,阵元C相对于阵元B的相位差可以表示为dycosφk/λ,阵元A相对于点O的相位差可以表示为dzcosφk/λ。其中dx,dy,dz分别为x轴、y轴和z轴上的阵元间距,λ为载波最高频率信号所对应的波长。

xoy面与zox面阵列接收信号数据可以分别表示为

Xx(t)=A(θ,γ)S(t)+Nx(t)

Xz(t)=A(φ,γ)S(t)+Nz(t)

(2)

其中

Xx(t)=[Xx11(t),Xx21(t),…,XxN1,Xx12,…,

XxN2,…,XxNN(t)]H,

Xz(t)=[Xz11(t),Xz21(t),…,XzN1,Xz12,…,

XzN2,…,XzNN(t)]H

分别为xoy面天线阵列与zox面天线阵列的N2×N维接收数据矢量;H表示这个矩阵的共轭转置;S(t)=[s1(t),s2(t),…,sK(t)]T为K×N维入射信号矢量矩阵。Nz(t)=[nz11(t),nz21(t),…,nzN1,nz12,…,nzN2,…,nzNN(t)]H为相对应xoy面和zox面的N2×N噪声矢量。

A(θ,γ)=[a(θ1,γ1),a(θ2,γ2),…,a(θK,γK)],A(φ,γ)=[a(φ1,γ1),a(φ2,γ2),…,a(φK,γK)]分别为xoy面和zox面的N2×K维阵列流形矩阵。

a(θk,γk)和a(φk,γk)(k=1,2,…,K)分别为A(θ,γ)和A(φ,γ)的第k个信源的导向矢量。

(3)

(βxk,ηxk)=[exp(-j2πdxcosθk),

exp(-j2πdycosγk)]

βzk,ηzk)=[exp(-j2πdzcosφk),

exp(-j2πdycosγk)]

2 MUSIC算法

MUSIC(Multiple Signal Classification)算法是将接收数据的协方差矩阵分离出信号子空间和噪声子空间,利用信号方向向量与噪声子空间正交的性质来构造扫描空间谱,实现信号的DOA估计[5-6]。

假设在窄带信号的前提下,若有K个互不相关的信号以不同的到来角入射到阵列天线的N个阵元上,且K

(4)

写成矩阵的形式,有

x(t)=AS(t)+n(t)

(5)

假设信号矢量与噪声矢量也互不相关,则输入数据x(t)的协方差矩阵Rxx为

Rxx=ARssAH+δ2I

(6)

式中,Rss为信号S(t)的相关矩阵(correlation matrix)[7],Rss=E[S(t)S(t)H];δ2是噪声方差;I为单位矩阵;H表示矩阵的共轭转置。对Rss作特征值分解,则当各信源相互独立时,可以证明这N个特征值中,有K个大于零,N-K个等于0；将Rxx特征值按其模值的大小排序,不妨设λ0>λ1>…>λK-1>λK=…=λN-1=δ2是Rxx的N个特征值,设这N个特征值对应的特征向量分别是q0,q1,…,qK-1,qK,…,qN-1,若将后面N-K个小特征值对应的特征向量为EN=[qK,qK+1,…,qN-1],则它们构成噪声子空间。再利用K个大特征值对应的特征向量构造出信号子空间,噪声子空间与信号子空间是正交的。即有

AH·EN=0

(7)

由此构造空间谱函数PMUSIC,并进行谱峰搜索：

(8)

其中,a(θ)表示入射角为θ的导向矢量。得到的PMUSIC的K个最大值所对应的θ值就是所估计的信源到来角。

3 数值仿真与计算

3.1 数值仿真条件

表1所列是双平面阵列的数值仿真条件,天线阵列位于远场区,阵元数为32,即每个平面阵列16个阵元,假定有两个信号入射到阵列上,阵元间距均取为最高频率信号波长的1/2,数据采样次数取为1 024次。噪声设为与信号互不相关的高斯白噪声。

表1 数值计算仿真条件

3.2 数值仿真计算与分析

两个三维到来角取为(60°,40°,65.9°),(70°,50°,76.1°)；图2～4是信噪比为10 dB时,利用xoy面的阵列估计的三维空间到达角与x轴夹角及y轴夹角分量谱峰图。其中,图3、4分别为将信号谱峰投影到zox面与yoz面的图形。

图2 xoy面阵列估计的三维DOA分量

图3 信号与x轴夹角的估计谱峰在zox面的投影

图4 信号与y轴夹角的估计谱峰在yoz面的投影

从图3和图4能看到在两个谱峰的一侧,还有一个较小的峰值,这是由于存在噪声的扰动的结果。但这一扰动对估计结果没有影响。数值仿真表明,随着信噪比的升高这一扰动的峰值点越来越低。

从图2～4可以看出,利用xoy面的平面阵列可以同时估计出到来角的两个角度分量。其中一个是与x轴的夹角,另一个是与y轴的夹角。

相应地利用zox面的天线阵列估计出三维到达角的两个分量,如图5所示。一个是与z轴的夹角,另一个是与x轴的夹角。这样对于三维到来角中的与x轴夹角这一分量,每个阵列面分别估计了一次。

图5 zox面阵列估计的三维空间DOA分量

4 三维空间到来角的参数配对

一般情况下,不同的三维空间到来角中间的参数是不同的,利用这一性质可以对三维空间到来角的参数进行配对,认为中间参数相同的角度参数便是同一个空间角的角度参数。利用这一性质可以初步实现三维空间到来角的参数配对。

表2是不同信噪比条件下两个到来角估计的仿真结果。信噪比在-3～12 dB,每隔3 dB取值,进行仿真估计出两个信号的三维空间DOA。

表2 不同信噪比条件下两个到来角估计值

从表2可以看出,随着信噪比的增加,信号到来方向的估计精确度也随着增加,信噪比高于6 dB时能够精确地估计出三维信号的DOA,信噪比在-3 dB时估计误差保持在5°以内。

5 结 论

利用双平面阵列天线进行三维空间到来角的DOA估计，并利用了此双平面阵列天线DOA估计特点实现了三维空间到来角的参数配对。该方法在低信噪比的情况下仍能提供较好的估计精度，同时，增加的一个平面阵列相当于使阵列天线的口径增加，增强了接收信号的稳定性。数值仿真证明了此阵列天线的可行性和有效性,为未来通信实现精确的三维空间到来角估计提供了一种新的思路及解决方案。

[1] 陈小龙,关键,黄勇. DOA估计算法性能分析及仿真[J]. 海军航空工程学院学报, 2009, 24(3):191-194.

[2] 黎子胜,张建华,周天,等. 基于L型阵列的二维CAAT算法的高分辨DOA估计[J]. 海洋测绘, 2007, 27(1):27-29.

[3] 张辉,李晓明,葛临东,等. 基于均匀圆阵的空时二维波达方向估计算法[J]. 信号处理, 2008, 24(5): 766-769.

[4] 王月瑜,郭黎利,刁鸣. 基于平面圆阵的二维测向精度分析[J]. 弹箭与制导学报, 2007, 27(5):283-288.

[5] LIBERTI J C, RAPPAPORT T S. Smart Antenna for Wireless Communications:IS95 and Third Generation CDMA Applications[M]. Upper Saddle River:Prentice Hall PTR, 1999:257-262.

[6] SCHMIDT R O. Multiple emitter location and signal parameter estimation [J]. IEEE Trans on Antennas and Propagation, 1986, 34(3):276-280.

[7] 张贤达. 矩阵分析与应用[M]. 北京:清华大学出版社, 2004:484-493.

[8] 叶中付,沈凤麟. 一种快速的二维高分辨波达方向估计方法——混合波达方向矩阵法[J]. 电子科学学刊, 1996, 18(6):567-573.