热力学关系的图形记忆法
2011-09-25吕申壮
吕申壮
(乐山师范学院化学与生命科学学院 四川乐山 614000)
热力学中有4个基本函数(热力学能(U),焓(H),Helmholtz自由能(A或F),Gibbs自由能(G))和4个状态参量(压力(p),熵(S),体积(V)和温度(T)),这些量之间存在一定的基本关系。其中最基本的公式包括:4个基本函数之间的关系、4个微分式、8个对应关系式和4个Maxwell关系式,共20个式子。在物理化学教材[1]中讲述热力学函数之间的基本关系式时,多采用数学上多元函数微积分原理来推求这些基本关系式,比较繁琐,数学基础较差的学生不易理解,只能靠死记硬背;而这些基本关系式比较相似,容易混淆。为了帮助学生记忆这些公式,人们做了许多探索。本文在参考文献[1-9]的基础上,设计了两种图:矢量图和弧线图。利用这两种图及一些简单规则,很容易记忆热力学基本关系式。
1 热力学函数关系式图形的提出
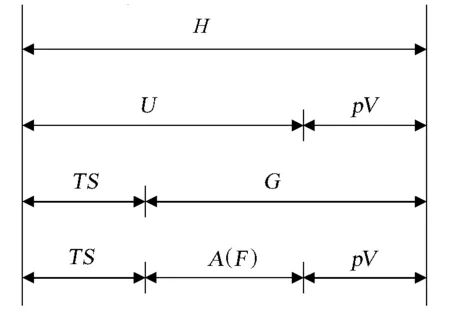
图1 热力学函数之间的关系
热力学函数之间的关系复杂,公式较多且相似,不便于记忆;而图形却直观、形象。因此,人们设计了多种图形来帮助记忆热力学函数之间的关系式。根据焓(H)、Helmholtz自由能(A或F),Gibbs自由能(G)的定义,人们设计了如图1所示的关系式图;但只利用了热力学函数的定义信息,只能反映出4个热力学函数之间的关系。文献[1]利用热力学第一定律和第二定律的联合表达式(dU=TdS-pdV)及定义式所得出的热力学函数的微分表达式,得到了如图2所示的关系图;但图2只能反映热力学函数的微分表达式,不能反映4个热力学函数(G,H,A,U)之间的关系。只要将图2边和角的元素依次顺移,再把对角线连接起来,利用矢量求和规则,就能同时反映出4个热力学函数之间的关系(图3A)。由于热力学函数本身不是矢量,因此,矢量的方向也可以全部反向。对于图3B所示的弧线图,利用图1最后一条横线,将TS和pV分开写在两个端点,由dA=-SdT-pdV可知,A的特征变量是T和V,将T和V写在紧靠A的端点,S和p写在远离A的端点。为了将图1中两条竖线用一点来表示,将表示G、H、A、U的直线改为弧线;为了顺序与矢量图一致便于记忆,将G和U写在下面,H和A写在上面,就可得到弧线图。由于热力学函数的其他关系(Maxwell关系、特征函数的特征变量、状态参数的偏微分表示)都可以由微分表达式推出,因此,加上一定的规则,由图3表示的图也就可以找到相应的关系式。
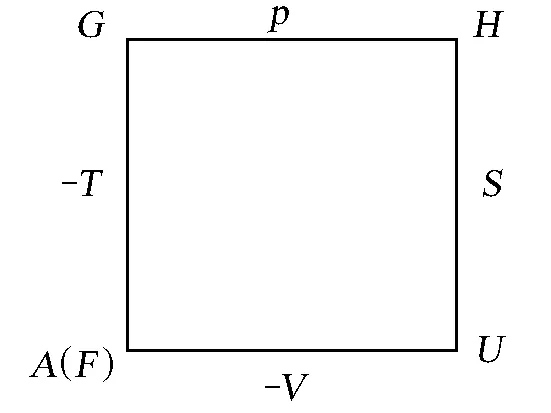
图2 热力学函数之间的关系图
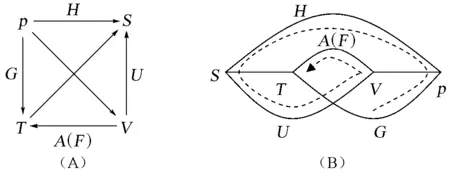
图3 热力学基本关系式的矢量图和弧线图(A)矢量图;(B)弧线图
2 图形本身的记忆方法
如图3所示,对于矢量图,将8个热力学变量从G到T依次排列为正方形,4个边分别为状态函数G,H,U和A(F),4个顶点依次为状态参量p,S,V和T。这个次序是按照人们精心设计的一句英语中每一个单词的首字母依次排成,即,“Good Physicist Have Studied Under Very Active/Able(Fine) Teacher”[1],意思是“杰出的物理学家曾师从极为优秀的老师”。矢量的方向按如下规定:对角线都是从强度性质指向广度性质(从左到右),正方形的边是指向右上角(S)或左下角(T)。由于热力学函数本身不是矢量,把上述规定的方向全部反向也是可以的。对于弧线图,弧线分别为状态函数G、H、U和A(F),4个顶点依次为状态参量S、T、V和p,从右下方的弧线开始,逆时针移动,其顺序与矢量图相同。
3 热力学关系式的记忆方法
3.1 4个状态函数之间的关系
根据图3给出的矢量图,规定对角线的两变量相乘,应用矢量的求和性质,作出图4。只看图4中虚线标出的部分,很容易得出状态函数之间的关系:
H=U+pV
(1)
同理可得出另外3个关系式:
G=H-TS
(2)
A=U-TS
(3)
G=A+pV
(4)
对于弧线图,规定将直线连接的两变量相乘,将弧线的两投影到直线上,就能得出上面的4个基本关系式。
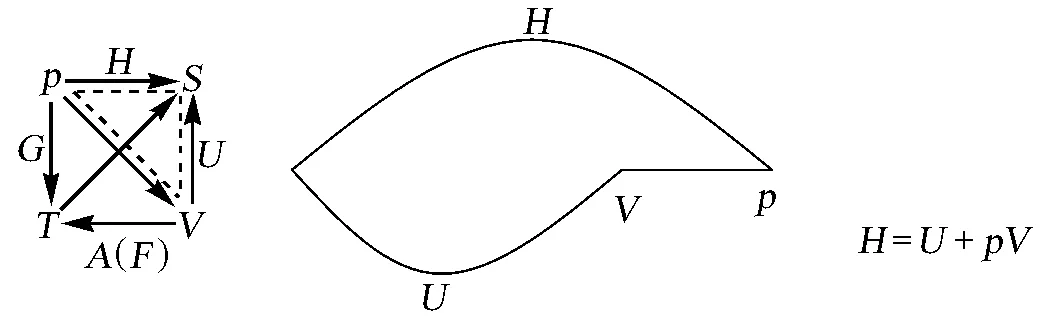
图4 4个状态函数的基本关系
3.2 特性函数及其特征变量
马休于1869年指出,对于U、H、S、A、G等热力学函数,只要其独立变量选择适当,就可以从一个已知热力学函数通过求偏微商,把一个均匀系统的平衡性质全部定下来。这个已知函数叫做特性函数,所选择的独立变量称为特性函数的特征变量。
记忆规律为,对于矢量图:每个边上的状态函数以它所在边上的两顶点的变量为状态参量时,此状态函数为特性函数,这两个状态参量就是该特性函数的特征变量。如:状态函数H所在边的顶点为p和S,则H=H(p,S)为特性函数。S和p为H=H(p,S)的特征变量。同理可得另3个特性函数:U=U(S,V),G=G(T,p),A=A(T,V)。对于状态函数S的特征变量,有两种选择方法,任选含S的一条边,S的特征变量是边上的量及该边的另一端点,S=S(H,p)或S=S(U,V)。对于弧线图:每条弧线连接的两个顶点就是相应的状态参量;任选含状态函数S的一条弧线,其特征变量就是弧线上的量及弧线另一端点的量。
3.3 热力学函数的微分表示
一个热力学系统的特性函数还可以用一个全微分方程来表示,这就需要记忆4个常用特性函数的微分表示。矢量图的记忆规则为:每一边上的的全微分等于两项之和,每一项是与该边连接的顶点的微分乘上该顶点的对角元,其正负号由对角线在该边上的投影是否与该边一致确定;一致为正,不一致为负。根据此规则(如图5所示),很容易确定以下的微分表示:
dH=TdS+Vdp
(5)
同理可得另外3个全微分表示:
dU=TdS-pdV
(6)
dG=-SdT+Vdp
(7)
dA=-SdT-pdV
(8)
弧线图的记忆规则为:每条弧线的的全微分等于该弧线的两个顶点的微分分别乘上与该顶点直线连接的另一顶点;每一项的正负号由弧线与直线的夹角确定,锐角为正,钝角为负。锐角表示弧线与直线延伸的方向是一致的,钝角表示弧线与直线延伸的方向相反。

图5 热力学函数的微分表示
3.4 Maxwell关系式
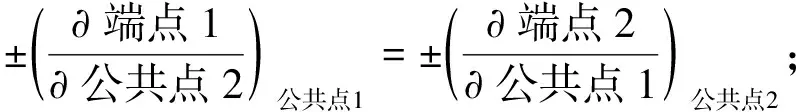
(9)
同理,可得到另外3个Maxwell关系式:
(10)
(11)
(12)
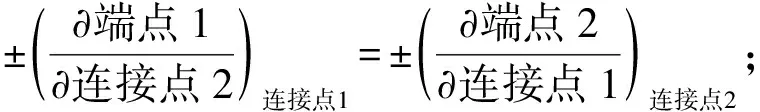

图6 Maxwell关系式
3.5 4个状态参量的偏导数表示

(13)
同理可得下面的偏导数表示:
(14)
(15)
(16)
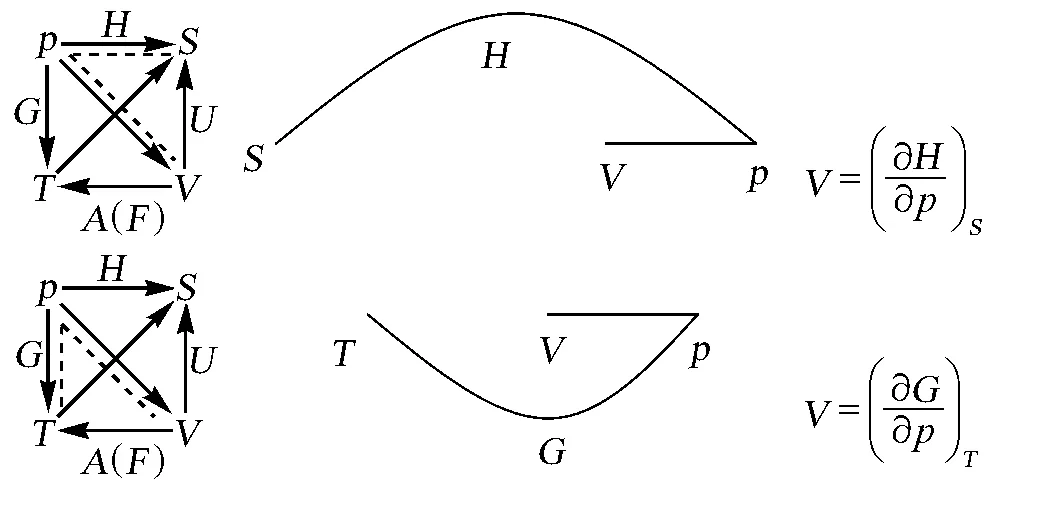
图7 状态参量的偏导数表示

4 结论
本文提出的两个图形能将热力学基本关系式有机地联系在一起,只要用心练习几次就能记忆热力学中的20个基本关系式。但此图形仅仅是能帮助记忆,不能代替推导。在学习物理化学时最好是经过推导,真正掌握物理化学中的重要概念和方法。
参 考 文 献
[1] 傅献彩, 沈文霞,姚天扬,等.物理化学.第5版.北京:高等教育出版社,2005
[2] 林朝金.四川师范大学学报(自然科学版),1995(6):96
[3] 阿里木江·艾拜都拉,开丽比努尔·艾山,朱玉军.北京教育学院学报(自然科学版),2007(2):5
[4] 韦薇.楚雄师范学院学报,2004(3):64
[5] 卢永智.陕西师范大学学报,2001(1):97
[6] 龙立平.益阳师专学报,1994(5):102
[7] 杨海莲,邹艳.榆林学院学报, 2007(6):41
[8] 魏鸿恩.西安建筑科技大学学报,1997(1):27
[9] 张兰知,谢学坤.哈尔滨师范大学自然科学学报,2002(2):31
