简论对称区间上的定积分题型

徐 健，张孔生

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

简论对称区间上的定积分题型

徐 健，张孔生

(安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030)

本文从微积分中具有或可转换成对称积分区间特征的定积分入手，得出求解定积分的一种考虑方法，从按此思路的求解可以发现，具有某些特征的定积分问题可以通过积分区间和被积函数的分解与合成得到一个新的易于求解的定积分．同时本文也推广到广义积分的形式．

微积分；对称积分区间；定积分分解合成

微积分中的积分问题是其重要的基础内容，而求解定积分则常出现在各种题目和各类问题的解决步骤中．在定积分里有一类积分区间是对称类型的题目，在解决这类问题中有些结论可以直接利用，但是通常情况下问题往往可能不适合使用已有结论，那么下面就针对这类问题进行分析．

1 例题求解及思路总结

微积分中有如下结论：若函数 f(x)为闭区间[-a,a]上的连续函数，当 f(x)为偶函数时有结论是采用负代换的方法通过定积分换元法结合奇偶函数性质来证明的，通常也采用奇偶函数对称图像来加以说明，在各种微积分教材中都有详细的说明，这里就不再赘述了[1]．下面直接来看一些例题：

(1)直接使用结论的情况[2]：

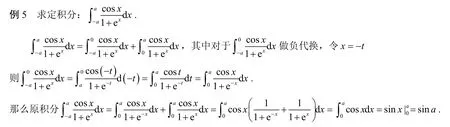
(4)当被积函数是非奇非偶函数时，往往可以有先拆后合定积分的方法[3]：上题中定积分虽然是一个对称区间的形式，但是被积函数却非奇非偶，而且也无法通过代数分解成奇偶函数的和，故而无法使用结论．但是又由于对称区间的原因此题可以将一个定积分分解成两个互为相反积分区间的定积分：这样可以通过负代换的方法把积分区间又统一成[0,a]，然后两个定积分就可以变为一个新的定积分，而这个新的定积分的被积函数又恰好可以化简，从而解决问题．

由此可以总结如下的思路：定积分的分解和合成可以有两种形式：一是被积函数的分解和合成，二是积分区间的分解和合成．如果一个定积分不好求解的时候，可以通过先拆后合的方法变换成一个新的定积分求解，往往会起到意想不到的效果．如例5中就是先积分区间的拆，然后被积函数再合．但是往往拆完要把两个定积分的积分区间统一，所以需要进行换元．下面由此思路来解决一些问题：

2 一些正常积分的解决

一些求解微积分的题目就可以利用上面总结的定积分分解合成思路来解决，这其中包括被积函数先分解如例6，以及积分区间先分解如例7：

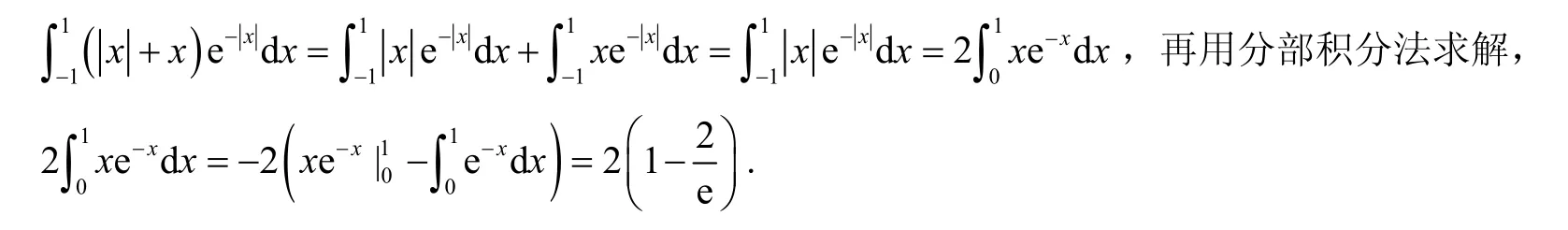
分析：此题如例 4积分区间不是对称区间，但易见被积函数中含有lnx，通常处理方法是分部积分法和换元法．这里使用换元法，令lnx=t，积分区间就变为对称区间．再如例 5先分积分区间变成两个定积分，再通过代换合成一个定积分求解．

通过上面的一些题目可以发现，对称区间是这一类题目的特征，但是互为倒数的积分区间也往往可以采用上面的解题思路，如例4和例7，下面的例8也采用先分解积分区间，再统一积分区间，最后通过被积函数合成一个新的定积分进行求解的．

综上所述当出现上面总结的积分区间特征的题型时，奇偶函数的结论不再适用，就可以采用以上考虑的思路求解，往往有意想不到的效果．特别注意如果要遇到广义积分时，题目往往也会出现类似上述的类型，但解决就要使用广义积分特有的思路，用极限的形式来表达，在各类微积分教科书中都有介绍，这里就不再重复了．

定积分求解的方法很多，题目也都比较灵活，在求解定积分的题目时更应该进行的是思路的总结、方法的提炼以及特征的提取，这样往往可以举一反三，掌握一类题型的求解．

[1] 李天盛.经济数学基础:微积分[M].西安:电子科技大学出版社,2002:245-303

[2] 费定晖,周学圣.吉米多维奇数学分析习题集题解(三)[M].济南:山东大学出版社,2003:309-336.

[3] 刘建宇.分割积分区间计算定积分[J].高等数学研究, 2009, 12 (6):31-32.

Abstract:This paper analyses some definite integral types that have symmetric integral interval. A new idea can be obtained.And we can find some definite integral types having the same characteristic can be solved by that idea. That is decomposition and combination of integral interval and integrand. Meanwhile this characteristic also can be generalized to improper integral.

Key words:Calculus; symmetric integral interval; decomposition and combination of integral.

(责任编校：李建明英文校对：李玉玲)

Analysis on Definite Integral in Symmetric Interval

XU Jian, ZHANG Kong-sheng

(School of Statistics & Applied Mathematics, Anhui University of Finance & Economics, Bengbu, Anhui 233030, China)

G642

A

1673-2065(2011)01-0073-03

2010-11-05

安徽省高校自然科学研究项目(KJ2010B001; KJ2010B007)

徐 健(1982-),男,安徽凤阳人,安徽财经大学统计与应用数学学院讲师,理学硕士;

张孔生(1978-),男,安徽青阳人,安徽财经大学统计与应用数学学院讲师,理学硕士.