辅助函数在定积分中的运用

2011-09-23吴丽崇孙凤忠

衡水学院学报 2011年1期

关键词：衡水等式结论

吴丽崇，孙凤忠

(1. 衡水职业技术学院经济管理系，河北衡水 053000;2. 衡水职业技术学院基础教学部，河北衡水 053000)

辅助函数在定积分中的运用

吴丽崇1，孙凤忠2

(1. 衡水职业技术学院经济管理系，河北衡水 053000;2. 衡水职业技术学院基础教学部，河北衡水 053000)

在定积分中，为了求得某些问题的解决，我们经常需要寻找某些证明方法，有的还需要构造与问题相关的辅助函数来研究其性质，从而得出欲证明的结论．构造辅助函数实质上就是分析法的一种技巧，在证明命题的过程中要不断研究问题的本质，从而寻找构造辅助函数的方法．

辅助函数法；定积分；分析法

构造函数法就是构造出与原命题相符且关系密切的函数，从函数的角度观察、分析、解释命题，沟通命题中条件与结论的内在联系，从而使命题(或问题)得以解决．

1 构造函数法解题的基本思路

构造函数法解题的基本思路如图1所示：

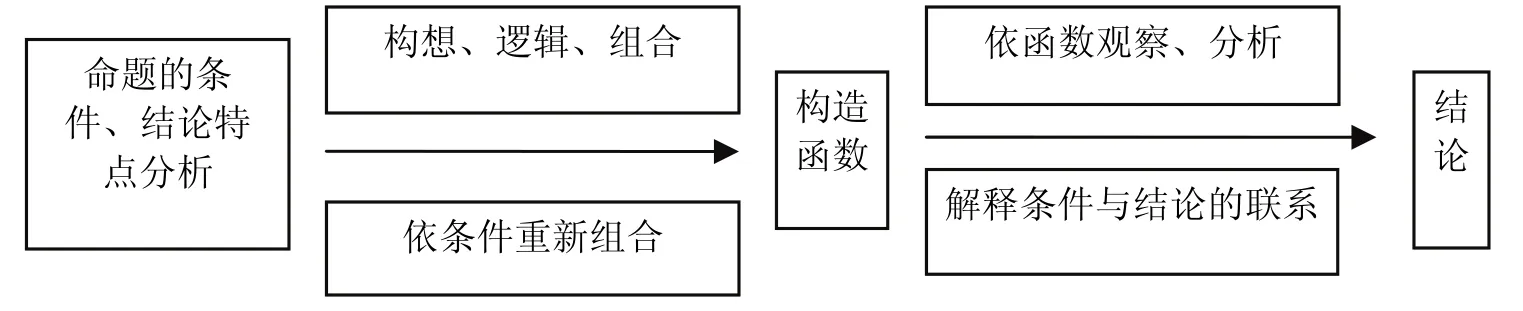
图1 构造函数法解题的基本思路

下面在定积分中讨论辅导函数的应用．

1.1 定积分等式的证明技巧

辅助函数法是定积分等式的一种证明技巧，适用于积分限中至少存在一点ξ或x0，使等式成立的命题的证明[1]．辅助函数F(x0)的作法如下：(1)将欲证结论中的(或x)改写成．(2)移项，使等式一端为零，则另一端即为所作的辅助函数F(x)．

1.2 定积分不等式的证明技巧

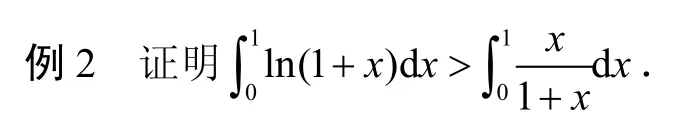
分析这里为证明积分不等式，我们可以引进一个辅助函数——相应的变限积分，把问题转化为用微分学的方法证明函数不等式．因此我们可以作辅助函数

这类题型的间接证明过程：先做辅助函数F(x)，验证F(x)满足零值定理，再由零值定理得出命题的证明[3]．辅助函数F(x)的作法如下：1)将欲证结论中的(或x0)改写成x．2)移项，使等式一端为零，则另一端即为所作的辅助函数F(x)．

2 结论

总之，辅助函数的构造离不开分析、推理和联想，解题时只有把知识学得系统、深入、融会贯通，才会取得事半功倍的效果．

[1] 翟延慧.利用构造函数法解题技巧[J].长春师范学院学报,2001(5):24-25.

[2] 范东林.例谈构造法解题[J].宿州师专学报,1999(2):61-63．

[3] 周玉平.高等数学中辅助函数的构造方法[J].扬州职业大学学报,2002(6):46-49.

Abstract:In order to figure out certain questions in definite integral, we need to seek certain proof method frequently, even create an auxiliary function related to the question to study its nature, thus draws the conclusion. In essence creating an auxiliary function is a skill of the analytic method, and we must unceasingly study the question’s essence in the propositionproving process, thus seek the method of creating an auxiliary function.

Key words:the method of auxiliary function; definite integral; analytic method

(责任编校：李建明英文校对：李玉玲)

Application of Auxiliary Function in the Definite Integral

WU Li-chong1, SUN Feng-zhong2

(1. Department of Economic Management, Hengshui College of Vocational Technology, Hengshui, Hebei 053000, China;
2. Department of Basic Teaching, Hengshui College of Vocational Technology, Hengshui, Hebei 053000, China)

O172

1673-2065(2011)01-0019-03

2010-09-08

吴丽崇(1984-),女,河北衡水人,衡水职业技术学院经济管理系讲师;

孙凤忠(1974-),男,河北景县人,衡水职业技术学院基础教学部讲师.