伪随机数质量对简单粒子群优化算法性能的影响

谭 阳

(湖南网络工程职业学院，湖南长沙 410004)

伪随机数质量对简单粒子群优化算法性能的影响

谭 阳*

(湖南网络工程职业学院，湖南长沙 410004)

伪随机数对粒子群优化算法的性能影响主要体现在算法种群多样性上。低质量的伪随机数会导致粒子群优化算法的性能出现不稳定的现象，通过对几种典型伪随机数的分析比较之后得出，粒子编码长度和伪随机数的周期的相互作用才是导致算法不稳定的原因。相关实验也验证了这一结果。

伪随机数;粒子群优化算法;种群多样性;海明距离

一、引言

通常把通过软件或数字电路实现一种确定性方法称为伪随机数算法，伪随机数因为其生成和使用十分方便，所以被广泛地应用于各种科学和工程领域。目前各种伪随机数发生器(pseudo－random number generator，PRNG)的类型很多，衡量其质量的高低主要通过各种统计检验来进行，其中Knuth和Diehard 是两个常用的统计检验集［1］［2］。粒子群优化算法 (Particle Swarm Optimization，PSO)是Kenney和Eberhart于1995年提出的一种智能优化算法［3］，PSO算法源于对鸟群和鱼群等群体运动行为的研究，与其他的演化算法一样也是一种基于迭代的优化工具;但相比较而言它具有算法简单，收敛速度快且对目标函数要求少等特点，通常PSO采用下式(1)的作为其标准算法:

Vi+1=c0vi+c1(pbesti－xi)+c2(gbesti－xi)

xi+1=xi+vi+1(1)

其中，式(1)中 i=1，2，…，N，N 为该群体中粒子的总数;vi是第i个粒子的速度向量;xi是第i个粒子当前的位置;c0，c1，c2为非负常数用以表示群体的认知系数，c0为粒子的惯性因子一般取(0，1)之间的随机数;c1，c2为粒子的学习因子一般取(0，2)之间的随机数;式(1)中的c1(pbesti－xi)部分被称为“认知”部分，表示粒子本身的思考，而c2(gbestixi)部分被称为“社会”部分，表示粒子间的信息共享与合作。每一维粒子的速度都会被限制在一个最大速度 vmax(vmax＞0) 内，即vi＞vmax或 vi＜ －max时，vi=vmax或vi=－vmax。粒子群的初始位置和速度随机产生，然后按照公式(1)进行迭代，直至达到最大迭代次数或找到满意的解为止。

作为PSO算法的主要步骤PRNG的重要性一直备受关注，传统观点认为应在PSO中采用质量更好的PRNG，以便促使PSO获得更好的搜索性能。但通过一些学者近年来的研究后表明，PRNG的质量的确能对PSO的性能产生影响但结果却与传统观点存在差异［4］－［7］，PRNG 质量的高低并不总是左右着PSO的性能;在某些情况下低质量PRNG的表现与高质量PRNG一样甚至更好，呈现出不稳定性。

二、PRNG对PSO性能影响的因素

在优化算法中所有使用了随机值的地方都会受到PRNG质量的影响，但本文经研究后发现对于PSO算法而言，随机值在迭代过程中并不大量地被使用，相对而言在PSO初始化的过程中PRNG对其影响更为突出。在PSO初始化的过程中PRNG的质量差异将直接影响PSO种群的多样性。类型充足且丰富的种群是PSO得以进行搜索的基础，多样性高的种群表现为个体粒子在解空间中的分布更为均匀，致使算法能在更大的范围内进行搜索;若种群类型不足，则导致种群在解空间中分布不均甚至形成团簇，这将直接限制粒子对解空间的搜索，从而导致PSO发生早熟收敛。图1表示种群的多样性对PSO性能存在显著影响。

图1 种群多样性对PSO寻优性能的影响

1.PRNG对种群多样性的影响及其度量方法

在演化计算中为了衡量算法种群的多样性，常使用计算并比较其种群海明距离(hamming distance)［8］的方法。不失一般性，若PSO种群为P，种群大小为N，采用固定长度为L的2进制对粒子进行编码。那么粒子空间B={0，1}L，种群P(P⊆B)为一有限点的集合，分别记 P中的粒子为:xi，x2，…，xn;若 xi(i=1，2，…，L)为 B 中的一个点，xi=a1，a2，…aL，则 al(l=1，2，…，L)，al∈{0，1} 被称为编码基因位。通常将任意两个粒子与xj(xi，xj∈B)之间的海明距离h(xi，xj)由下式(2)定义:

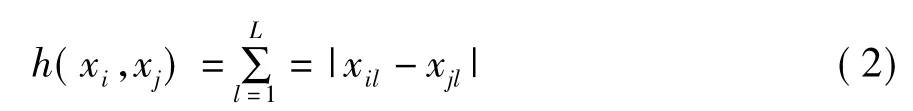
其中xil表示粒子xi的第l编码基因位。由式(1)可知 0≤h(xi，xj)≤L，h(xi，xj)=h(xj，xi)即 h是对称的，且只有在xi=xj时h(xj，xi)=0。若对采用均匀随机初始化的种群P0来说，种群中的粒子之间应该是相互独立且任意个体服从分布P{X=x}=1/2L;粒子的任意编码基因位取值0或1的概率相等(p=q=0.5)且相互独立。粒子xi与xj间的海明距离h(xi，xj)服从参数为L和P的二项分布，即h(xi，xj) ～B(L，p);期望值 E(h)=Lp=L/2;方差 D(h)=Lpq=L/4。

只衡量2个独立粒子的海明距离并没有太多数学意义，为了能在各种大小的种群P之间进行多样性度量，这里定义Da(P)为对种群P中任意粒子的平均海明距离:

Dh(P)为种群P中任意2个粒子间海明距离的总和。由式(3)可知，0≤Da(P)≤L只有当种群为齐次种群(指种群中所有粒子的值完全相等时，通常意味着PSO算法已经停滞或已找到最优值)时Da(P)=0。对于均匀随机初始化的种群P0来说Da(P0)是随机的，并且Da(P)会随着PSO搜索过程中种群多样性的下降而下降，最终种群收敛为齐次种群时Da(P)=0。

2.PRNG对粒子周期的影响及其度量方法

在统计中若种群P中的粒子循环周期为m，则表现为在经过m个粒子长度之后会产生与之前完全相同的粒子;即这一种群中存在对任意粒子xi都有xi=xi+m的关系。在PSO中若经PRNG随机生成的独立粒子产生重复，这将直接导致种群多样性的下降，致使PSO算法恶化。通常若PRNG拥有足够长的周期T，PSO在初始化种群的过程是不可能用到超过PRNG单个生成周期数量的随机数的，因此通常PRNG不会产生循环。但若采用短周期的PRNG则会使得PSO在初始化中容易产生循环，导致种群多样性直接受到影响。若PRNG的周期长度为T，用其对固定长度 且采用二值编码的种群的周期的影响如下式(5)所示:

其中m为该PRNG对于固定长度为L的种群循环周期，lcm(T，L)为T和L的最小公倍数。

三、仿真实验

1.实验方法

为了方便对比，本文采用三种PRNG来进行测试［1］:第一种是 Mersenne Twister(MT)，其周期长度为且在高达623维的空间中分布均匀，是目前学术界公认的最好的PRNG之一;第二种是普通长整形的线性同余方法Linear Congruence(LC)，其周期为232－1;第三种同属于MT算法，但是其周期被人为固定为1000，这里将其称之为MT1000;该PRNG在产生1000个随机值后会使用固定数值的种子进行重设，是一种典型的低质量的 PRNG，文献［4］［5］都曾使用其作为对比之用。测试函数采用陷阱函数Shubert其表达式如下式(6)所示:

图2为Shubert函数在MATLEP中的模拟仿真图像，该函数有9个全局极小值且这9个全局极值点呈规律分布;该函数常用于检验优化算法的种群多样性。

图2 Shubert函数的模拟图像

具体操作方法为，对种群中所有粒子分别按200、199、500、503共四种不同长度来进行二值编码。并且始终固定粒子种群数目为;分别固定式(1)中的认知系数为 c0=0.5、c1=2、c2=2;PSO最大迭代次数为2000。使用前文提到的三种PRNG来对四种不同编码长度的粒子实行初始化;再使用不同编码不同初始化的12种PSO分别对Shubert函数进行5次优化，记录所有迭代过程中每代的平均海明距离Da(P)，并取相同代数的平均值。

2.实验结果

传统观点认为PRNG的循环将引起PSO性能的降低。但实验表明，PRNG发生循环并不一定会导致PSO性能的降低，在某些情况下也会获得很好的性能。图3为在四种不同编码长度下PSO种群多样性的对比。

3.结果分析

图3 三种PRNG在不同编码长度下的种群多样性

在观察对比MT、LC和MT1000时可以发现MT和LC在图3中所有编码情况下，两者表现基本一致，虽然MT和LC在自身周期长度上差异巨大但是对PSO种群多样性的影响上却微乎其微。但是在通过图3中对MT1000的观察中却可以看到两种截然不同的结果:第一种如图 3(a)、3(c)所示，MT1000对比MT和LC在影响PSO种群多样性上的差异明显，通过前式(5)可知 取值与 与 有关，当时，这时MT1000初始化的粒子循环周期;而当时。很小的粒子循环周期将导致种群中出现大量的同质粒子从而致使Da(PMT1000)的取值下降。第二种情况如图3(b)、3(d)所示，MT1000对PSO的种群多样影响相对较小，甚至在部分区域还出现了优于高质量PRNG的情况。可以看出当L=199和L=503时虽然与L=200和L=500和 数值差距不大，但是199和503均为素数，这就使得在这两种编码长度下的mMT1000取值要远高于编码长度为200和500的情况。

由此可知，短周期PRNG使PSO性能在粒子编码长度不同时呈现出不稳定性，其原因在于个体循环周期的取值存在差异性，导致种群多样性呈现不同的变化模式，从而影响PSO性能。m越小，则PSO种群多样性下降幅度越大，导致PSO性能也将大幅下降;反之，m越大，则PSO种群多样性下降幅度越小，PSO的性能也将越好。

四、结论

本文的研究结果表明，低质量的PRNG主要通过初始化来影响PSO种群的多样性从而使得PSO性能表现出不稳定。但就本文的实验结果而言，表明质量稍低甚至质量一般的PRNG也能获得与高质量PRNG基本一致的性能，与文献［9］提出的应当选用当前质量最好PRNG的建议有所不同，本文认为高质量的PRNG算法对PSO算法所带来的收益并不明显，相反其系统开销却较大。对于简单的PSO更应考虑在可行性和经济性的前提下适度提高PRNG的质量。

［1］Knuth D E.The Art of Computer Programming［M］.USA:Addison－Wesley，1998.

［2］Marsaglia G，Zaman A.A New Class of Random Number Generators［J］.Annals of Applied Probability，1991，1(3):462－480.

［3］Kennedy J，Eberhart R C.Particle Swarm Optimization［C］.Proc IEEE International Conference on Neural Networks.Piscataway，NJ:IEEE Service Center，1995:1942－1948.

［4］Meysenburg M M，Hoelting D，McElvain D，et al.How Random Generator Quality Impacts GA Performance［C］.Proceedings of the Genetic and Evolutionary Computation Conference，2002.San Francisco USA:Morgan Kaufmann Publishers，2002:480 －487.

［5］李东，汪定伟.基于仿真的优化方法综述［J］.控制工程，2008，15(6):672 －677.

［6］江维，沈斌，胡中功.微粒群算法参数的理论分析［J］.化工自动化及仪表，2009，36(4):38 －40.

［7］朱奇光，王洪瑞.IC－PSO算法的收敛性分析及应用研究［J］.光电工程，2010，37(4):108 －112.

［8］Mattiussi C，Waibel M，Floreano D.Measures of Diversity for Populations and Distances Between Individuals with Highly Recognizable Genomes［J］.Evolutionary Computation，2004，12(4):495－515.

［9］Cantú －Paz E.On Random Numbers and the Performance of Genetic Algorithms［C］.Proceedings of the Genetic and Evolutionary Computation Conference，2002.San Francisco USA:Morgan Kaufmann Publishers，2002:311 －318.

Abstract:Pseudo－random number on the performance of PSO algorithm is mainly reflected in the diversity of the population.Low－quality pseudo－random number will lead to the performance of PSO instability phenomenon，through the typical pseudo－random number drawn after analysis and comparison of the particle and pseudo－random number code length interaction cycle is the result algorithm for the cause of instability.Experiments also confirmed this result.

Key words:pseudo －random number，particle swarm optimization，species diversity，hamming distance

On the Impact of Pseudo－random Number Quality on Simple Particle Swarm Optimization Performance

TAN Yang

TP301.6

A

1009－5152(2011)01－0048－04

2010－11－26

湖南省自然科学基金(06JJ50107)。

谭阳(1979－ )，男，湖南网络工程职业学院讲师，工程师。