二维矢量声强探头的设计计算与误差修正

周广林, 郭秀艳

(黑龙江科技学院 机械工程学院,哈尔滨 150027)

二维矢量声强探头的设计计算与误差修正

周广林, 郭秀艳

(黑龙江科技学院 机械工程学院,哈尔滨 150027)

一维声强探头测量二维空间方向声强需要测量两次,费时且有时时间上不允许。利用平行四边形曲柄机构的位置保持原理,设计了测量频率范围可调的二维矢量声强探头的机械结构。基于双传声器互谱声强法原理,采用三个传声器构成的二维矢量声强探头,给出了二维矢量声强的测量原理、二维矢量声强的计算公式和有限差分误差修正方法。修正后互谱声强计算值和理论值之间的误差要比修正前显著减小,表明有限差分误差修正方法可以明显降低互谱声强测量中由于有限差分导致的声强测量误差。

二维矢量声强探头;结构设计;误差分析;误差修正

Abstract:Aimed at an alternative to one-dimensional sound intensity probe suffering from the twice measurement of two-dimensional spatial sound intensity,with resulting time-consuming and time-limited process,this paper introduces the design of the mechanical structure of two-dimensional vector sound intensity probe with the adjustable measuring frequency range by using position holding principle of parallelogram crank mechanism,proposes the two-dimensional vector sound intensity probe consisting of three microphones,based on two-microphone cross-spectrum sound intensity theory,and features two-dimensional vector sound intensity measurement principles and formulas,and finite difference error correction method.The cross-spectrum sound intensity shows a significantly smaller error be tween the calculation value and theoretical values after the correction than before the correction,confirming that the finite difference error correction method allows a significant reduction in the error arising from finite difference in the cross-spectral sound intensitymeasurement.

Key words:two-dimensional vector sound intensity probe;structure design;error analysis;error correction

声强是矢量,有时需要知道空间三维或二维方向的声强,以确定声能流的方向。若用一维探头就需要在同一点上按三个方向测量三次、二个方向测量二次。这比较费时,有时测量尚未结束,工况就变化了,所以开发能同时测出三维或二维矢量声强的仪器很有必要。目前,国内外关于三维矢量声强探头已有研究。丹麦 B&K公司生产的WA0447型三维矢量声强探头,是采用三对传声器对六个通道同时采样、一次测量三个方向的声强测量仪器[1]。日本的Nittobo声学仪器公司研制的MT ver2.0声强探头旋转装置,安装 B&K4181型声强探头,使其沿着两个紧密结合的圆形导轨旋转探头就可以测量出x、y和 z三个方向的声强矢量。这种测量方法保证了空间精度,但只能用于稳态声场[2]。Hideo Suzuki等开发了用四个传声器组成的新型三维矢量声强探头[3]。陈心昭等研制了一种由四个传声器组成的三维矢量声强探头,并申报了国家专利。此声强探头结构简单,可保证测量时的空间定位精度,一次测量即可获得声场中三维矢量声强[4-5]。

鉴于二维声强探头可以测量声强分量且国内外研究的比较少、尚无成型的二维矢量声强测量系统,研制一种平面二维矢量声强探头对二维矢量声强测量系统的开发起着非常重要的作用。

1 探头的结构设计

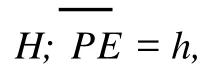
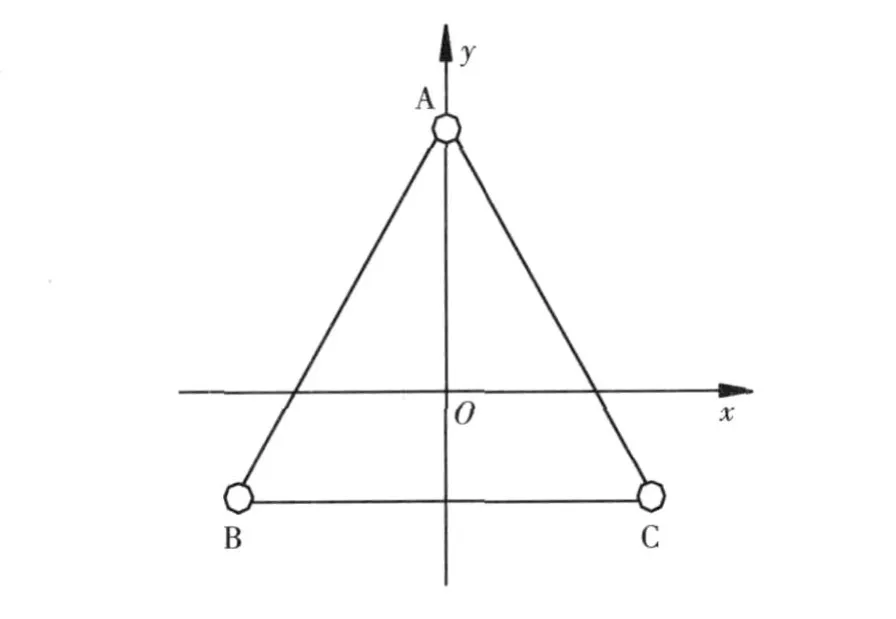
图 1 新型二维矢量声强探头中传声器的放置Fig.1 Three m icrophone arrangement for new type 2-D probe

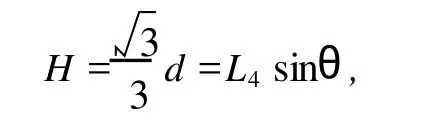
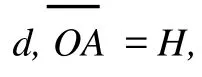
即传声器中心

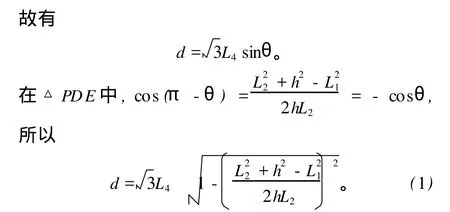
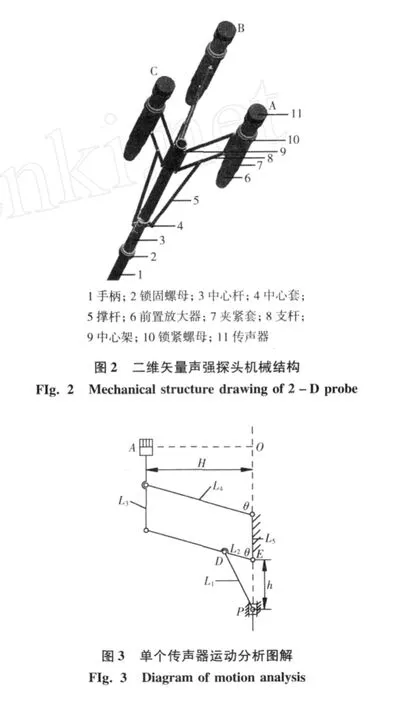
由于 L1、L2、L4均为定值,故传声器间距 d随 h的变化而变化。可以看出,随着 h的均匀变化,传声器间距 d的变化却是不均匀的,即传声器间距均匀变化时,中心套移动的距离是不相等的。为直观显示传声器间距,以便于测量和计算,根据式 (1)计算出传声器间距与中心套位置的关系,在中心杆上标记刻度线以对应几个基本间距,如图 4所示。

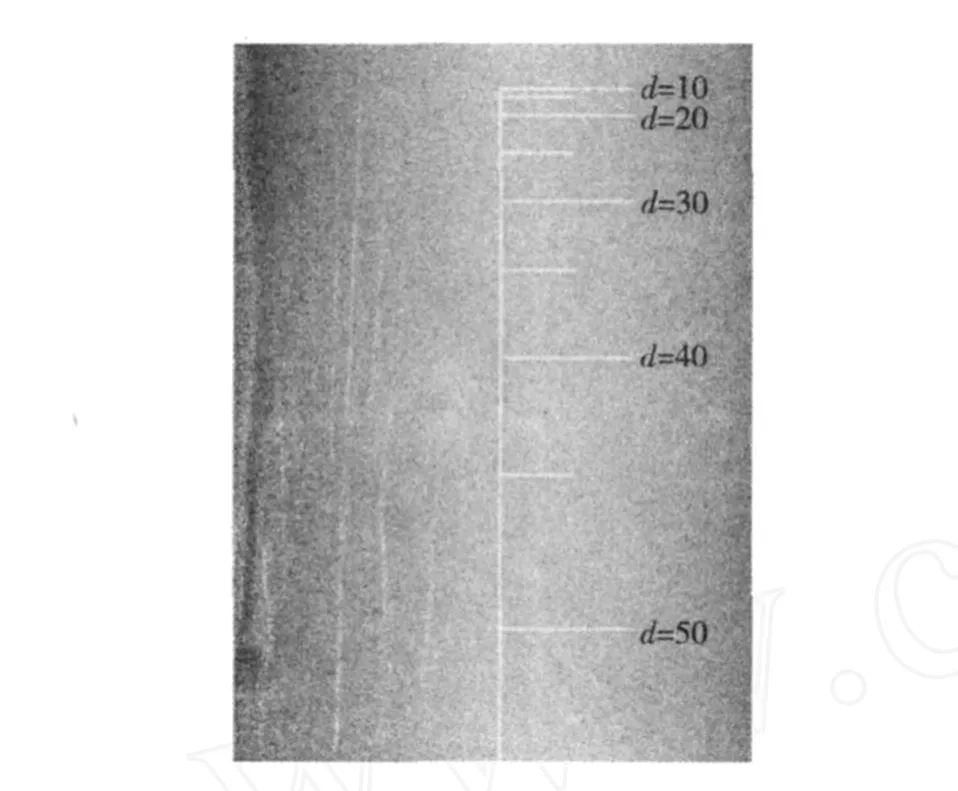
图 4 中心杆上刻度线放大图Fig.4 Enlarged drawing of graduation line in centrol pole

2 声强的计算方法

根据图 3,三个传声器分别放置在正三角形三个顶点处,重心点处的声强矢量可由 x、y方向的声强分量合成。为计算重心点处 x、y方向的声强分量,首先求正三角形重心处的声压 p0

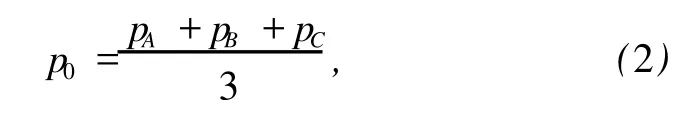
式中:pi(i=A,B,C)——第 i个顶点处的声压。

连接各顶点和重心朝着重心方向的声质点速度ui(i=A,B,C)由平均声压 p0和各顶点声压 pi的线性近似表示为

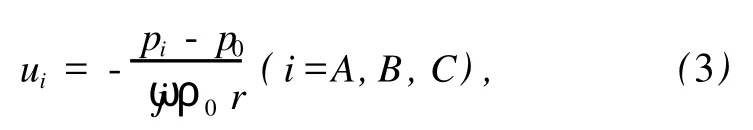
式中:r——重心与顶点之间的距离。

根据如图 5所示的正三角形几何关系,可以得到 ui(i=A,B,C)与重心处的声质点速度在 x、y方向上的分量 ux、uy间的关系如下[6-7]:

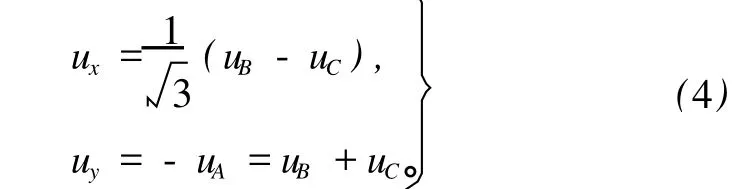
结合式(2)～(4)并根据互谱声强法原理得重心点处的声强在 x、y方向分量

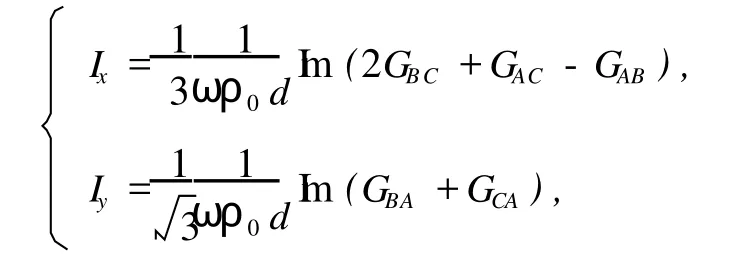
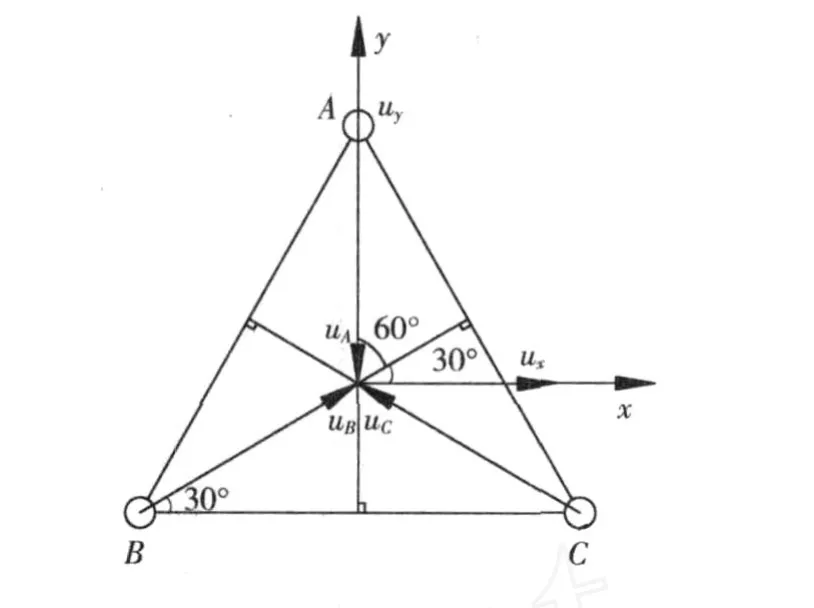
图 5 传声器位置与 x,y坐标图解Fig.5 M icrophone arrangement andx,y coordinates illustration

式中:Gij——第 i个顶点与第 j个顶点处声压的互谱。

由此可得重心点处的二维矢量声强大小及方向

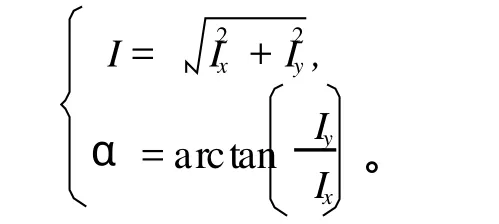
为了分析二维矢量声强的测量误差情况,定义声强测量结果 I与其理论值 I0的误差函数为以分贝表示的声强级误差Le=10 log(I/I0)。文献[8]以平面声场和单极子、偶极子声场为例,分析了声强误差和声源的定位误差,证明了二维声强探头测量声强的有效性,并且能够快速地定位声源。

3 声强的误差修正方法

文献[6,8]主要是各点主声强 (沿着声场中的质点振动速度方向的声强)方向的有限差分误差值。该方向是声场中声能量流动最快的方向,受到声场本身和测量的限制,不能始终保证声强测量时声强探头轴线和声波传播方向始终保持一致。当声强探头轴线与波阵面法线存在倾斜角θ时[6],存在

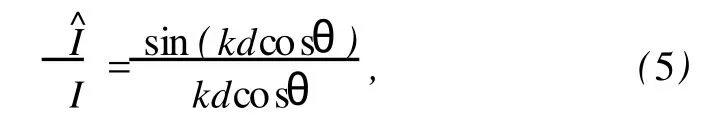
k——声波波数。

平面声场中任意一点的声强可以用沿着直角坐标系 x、y轴方向的两个声强分量唯一表示,与主声强矢量的关系为

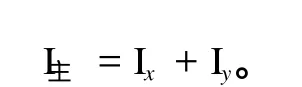
主声强幅值和两个沿着坐标轴的声强分量的幅值之间满足关系:

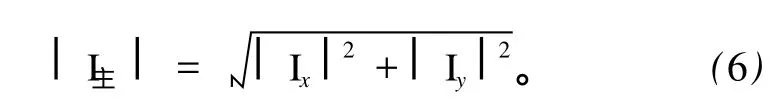
明显,只要测量到声强分量 Ix、Iy后就可以计算得到主声强 I主值并唯一确定主声强矢量 I主与 x、y坐标轴之间的夹角,也就是可以确定过该测量点的波阵面的法线方向。

把主声强 I主与 x、y两个坐标轴的之间的夹角分别记做α、β,按照声强矢量分解与合成,有以下的关系存在:

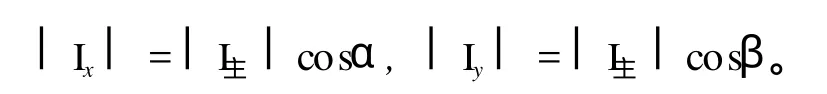
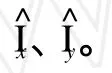
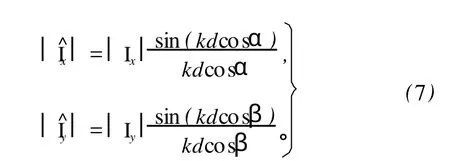
表示为

从此可以看出,有限差分误差与探头在声场中的方位α、β有关。

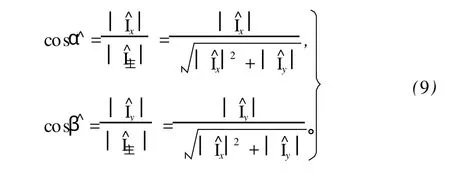
把式 (7)和 (8)代入式 (9),可得

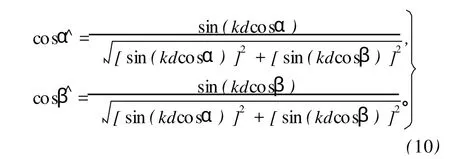
由式(10)可知:通过平面二维声强矢量测量值估算出来的方向余弦值 cosα^,cosβ^与该测量点声强的理论值无关,只与所测量的声波的波数 k、两个传声器之间的间距 d、方向余弦的真值 cosα、cosβ有关。这说明对一个确定声场中互谱声强测量,方向余弦的估算值与声强本身的大小无关,不会因为声场本身强弱的变化而影响方向余弦的估算精度。

以上讨论证明了通过二维矢量声强的互谱测量值可以估算出该点主声强的方向余弦,进而可对互谱声强测量值中的有限差分误差进行修正。

平面二维矢量声强测量的有限差分误差修正实现步骤为:

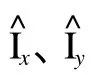
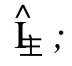
(3)由主声强方向余弦的估算式 (9)计算出主声强与两个坐标轴之间的方向余弦估算值

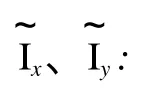
从误差修正的步骤来看,整个误差修正过程简单且容易实现。这种修正方法是一种方便快捷的修正方法。下面以单极子声场为例来说明这种有限差分误差修正方法对声源频率的适应性,得到 x、y方向上修正前后的声强级误差曲线如图 6所示。

由图 6可见,经过修正互谱声强计算值和理论值之间的声强级误差要比修正前显著减小。频率在5 kHz以下时,修正后 x、y方向上的声强级误差均小于 0.6 dB,表明利用上述有限差分误差修正方法可以降低互谱声强测量有限差分导致的声强测量误差。

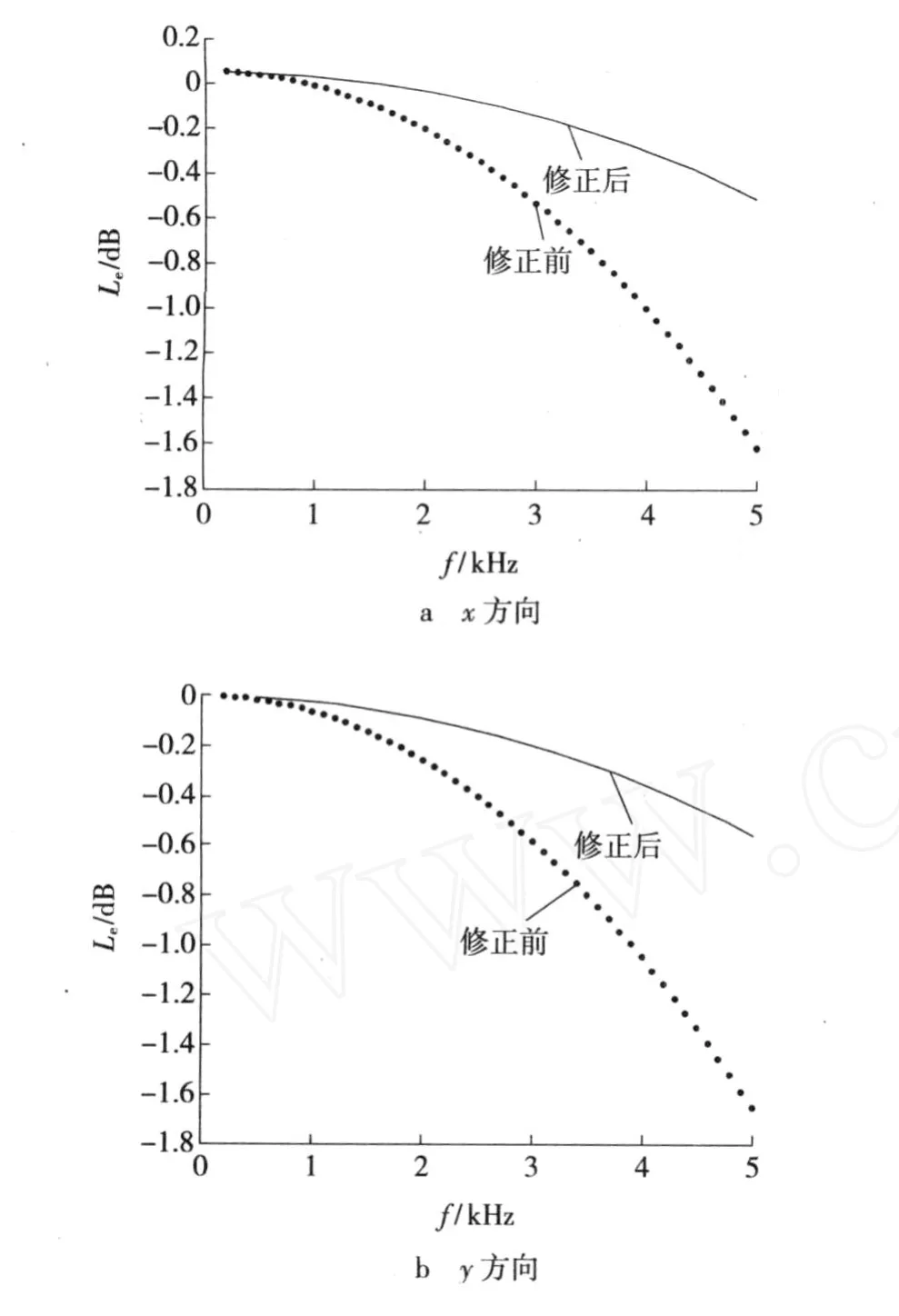
图 6 修正前后的声强级误差曲线Fig.6 Error curves of sound intensity level of pre and post correction

4 结 论

(1)利用曲柄机构和平行四边形的位置保持原理,设计出一种二维矢量声强探头的机械结构,实现了其测量频率范围可调的功能。

(2)设计了一种由三个传声器组成的二维矢量声强探头结构,能够有效地测量出声场的二维矢量声强,可以进行声源定位。

(3)传声器间距对测量误差有重要的影响,测量高频噪声时应采用较小的传声器间距。

(4)有限差分误差修正方法可以明显降低互谱声强测量中由于有限差分导致的声强测量误差。修正后互谱声强计算值和理论值之间的误差要比修正前明显减小。

[1] WASER M P,CROCKER M J.Introduction to the two-microphone cross-spectral method of determining sound intensity[J].Noise Control Engineering Journal,1984,22(3):76-85.

[2] JACOBSEN F.Random errors in sound power determination based on intensity measurement[J].Journal of Sound and Vibration,1989,131(3):475-487.

[3] H IDEO S,SHUN O,MASAZON A,et al.A three-dimensional sound intensity probe[J].Journal of the Acoustical Society of A-merica,1992,91(4):2 370-2 372.

[4] 周晓峰,毕传兴,孙 彪,等.一种新的三维矢量声强测量方法[J].计量学报,2007,28(4):297-301.

[5] 孙 彪,毕传兴,陈心昭.新型三维声强虚拟测量分析仪[J].农业机械学报,2007,38(6):147-150.

[6] 郭秀艳.二维矢量声强探头研究[D].哈尔滨:黑龙江科技学院,2010.

[7] ZHOU GUANGL IN,GUO X IUIYAN.Two-dimensional sound intensity probe and error analysis[C]∥CU I J IANP ING,Q I J IMI NG.Proceedings of 9th International Conference on Electronic Measurement&Instruments.Beijing:Institute of Electrical and E-lectronics Engineers,Inc,2009:427-431.

[8] 周广林,郭秀艳.二维矢量声强的误差分析[J].黑龙江科技学院学报,2009,19(5):348-351.

[9] 陆益民.互谱声强测量误差分析及修正方法研究[D].合肥:合肥工业大学,2008.

(编辑 晁晓筠)

Design method and error correction of two-d imensional vector sound intensity probe

ZHOU Guanglin, GUO Xiuyan
(College ofMechanical Engineering,Heilongjiang Institute of Science&Technology,Harbin 150027,China)

TB95

A

1671-0118(2011)01-0064-05

2010-12-03

国家自然科学基金项目(50575063);黑龙江省研究生创新科研项目 (YJSCX2009-065HLJ)

周广林 (1961-),男,吉林省怀德人,教授,博士,研究方向:机械低噪声设计,E-mail:guanglinzhou@163.com。