400000 DWT矿砂船的全船和局部振动研究

张新伟 陆利平 吴小康

（上海船舶研究设计院，上海 200032）

0 引言

400000 DWT超大型矿砂船CHINAMAX是由上海船舶研究设计院（SDARI）为国际三大铁矿石巨头之一的巴西淡水河谷矿业有限公司开发的一种新船型。虽然现在一般的振动研究都集中于类似于集装箱船、LNG等振动要求高、振动灾害频发的船型，但是作为世界上最大矿砂船CHINAMAX的首制船，船东对振动计算提出了非常高的要求。本船型由于自身吨位过大的特点，故的确有可能存在比较严重的振动灾害。

首先，本船型考虑到经济性，在同类船舶比较中航速较快，所以选用主机功率大、质量大，输出力矩也比较大。原始设计中由于发动机厂商的推荐，主机双侧均未加横撑，故留下了比较大的安全隐患，必须计算加以验证。

在现有实船中，桥楼甲板两翼由于进港等操作要求需要，按照规范必须延伸到舷侧，延伸长度一般很长，结构上异常薄弱，就引发了很多振动问题。本船该问题尤其明显。为满足舾装数的要求，桥楼甲板处上层建筑宽度仅有15.2 m，使两翼长度各达到了创记录的24.5 m，故必须精细计算该处的振动性能。考虑到作为震源的螺旋桨和主机发出的激励传递到两翼，要涵盖尾部、机舱、上层建筑等几乎所有区域。所以，本船型要求精细建模计算的范围是比较广的。

由于本船吨位大，全船大部分区域型材尺寸都很大，所以螺旋桨和主机作为常规振源，对本船大部分的结构影响是很有限的。但是大吨位船舶固有频率肯定非常低，重要海浪的固有频率一般为0.02～0.80 Hz之间，这样海浪的弹振和拍振对于本船型中部型材疲劳寿命将会有非常大的影响。船东提出在挪威MARINTEC针对本船型做海浪的弹振和拍振实验。作为实验的关键数据，必须在先期精确计算出本船型满载和压载条件下的两节点垂向固有频率。

基于本船型这些特点和船东的要求，就要求通过全船有限元分析来校核全船振动特性和尾部、机舱、上层建筑等部位的直接振动预报；并且还要对重点部位进行局部模态分析以避开主要激励源频率。

该船主要设计参数如下：

1 有限元模型

有限元模型采用SDARI引进的大型有限元建模计算软件PATRAN/NASTRAN建立。有限元模型品质是决定振动计算准确与否的最关键因素。根据计算要求的不同，对模型品质的要求也是有很大差异的。本船因为要求计算出整个尾部（包括船尾、舵、上层建筑、机舱）的响应特性，所以必须对这个区域要求精细建模得以反映出这个区域所有的结构细节。另外，本次计算还要担负给弹振和拍振实验提供精确的全船两节点垂向固有频率的任务，所以货舱区和首部虽然不用精细建模，但是也不能像普通振动计算那样用一根船体梁来模拟。

计算要求确定下来，有针对性的模型要求也随之确定下来。主船体板（如甲板、舱壁、围壁、肋板、外板等）采用3节点或者4节点板单元模型；桁材，扶强材以及加强筋采用带有弯曲要素的梁单元模拟；一些特殊结构如尾部铸钢件采用体单元模拟，并且用MPC连接解决体单元、板单元自由度不匹配的问题［1］。

网格大小对于前面所述细化区域采用纵骨间距X肋距以期尽可能反映所有结构细节。对于货舱区和首部采用强框间距的网格尺寸使之在不失精确度的前提下最大可能节省计算机和人力成本。具体模型参照图1、图2。

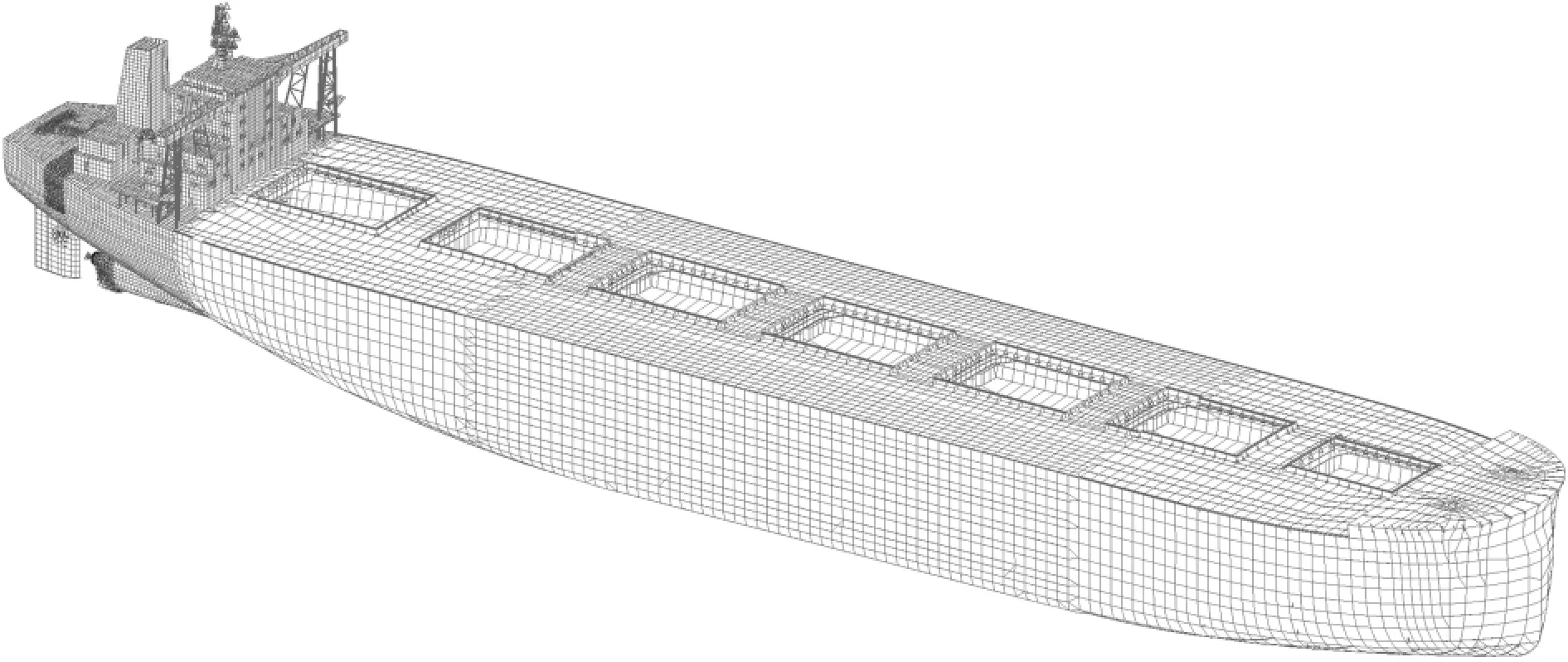
图1 总体模型图

2 模型质量分布

振动计算不仅要考虑结构刚度，还要考虑船舶质量，两者对于振动计算结果的影响是并重的。从质量组成考虑，模型可以分为空船质量和装载质量两大类考虑。空船质量又可以分为结构质量和非结构质量两类。装载质量也必须分为满载质量和压载质量两类载况加以分析，然而无论哪种载况，装载质量又都必须考虑船舶载重量和船体表面附加的水质量。下面分别加以分析。

模型细化部分对于质量模拟的仿真度要求是非常高的。基于此，该部分模型的结构质量不采取任何常规配重的方法，比如修改不同部位的结构密度、配点质量等方法。本文对于此部分结构质量采用了开孔板厚折减、板缝线平均板厚等方法用以仿真结构质量的空间分布。成品模型经过测算，有限元结构质量仅比实船小2%，但是船体模型空间刚度和质量的分布应该是得到了较好的模拟。对于货舱区和首部的粗模区域我们采取了调整该区域密度分布的方法使之结构质量和实船基本一致，并且质量分布也能一定程度上满足工程计算要求。

船舶质量不仅有钢组成的结构质量，也包括甲板敷料、舾装件、轮机件等非结构质量。这些非结构质量即可以采用板、梁等单元自带的用单位面积（长度）附带质量表述的非结构质量模拟，也可以用质点质量模拟。具体采用哪种方法可以灵活运用，但基本原则是一要尽可能模拟质量的空间分布（质心分布），二是避免大质量区域集中以免计算时出现质量突变造成结果失真。

主机的模拟也是这次计算的重点。为了真实反映主机机架的刚度特性，现在有些船级社如GL开发出较为成熟的软件。该软件采用平面应力单元将柴油机的内部结构很好地模拟出来并且实现了模块化。使用时可以很方便地将主机有限元模型整合到整船模型中去，就可以不仅方便求解振动响应时激振力矩的施加，也能准确计算出主机机架和双层底组成系统的固有频率，看有无和主机激励发生共振的可能性。对于SDARI而言要做到这条并不容易，因为获得主机厂商的主机结构图纸是不太现实的。但是对于大型低速柴油机而言，主机机架的结构刚度对于计算结果可以说无关紧要。由于主机质量非常大，刚度也很大，所以振动时发生的将是近乎纯弯曲型振动而非剪切型振动。这种类型的振动起决定因素的是支撑结构的刚度而不是振动结构物本身的刚度。应用到这次计算中起决定因素的是双层底的刚度而不是主机机架本身的刚度，即使将主机模拟成刚体也仅仅会带来最多5%的误差［2］。基于这条原理，我们用板、梁、点单元来模拟主机机架，保证总刚度、外形尺寸及质心三向坐标和主机规格书中一致，并且对主机和双层底组成系统做局部模态分析以保证主机振型呈近刚体状。

装载质量的变化对于船体振动模态会产生非常大的影响。目前国际上对于振动计算都要求针对满载和压载两种极端载况分别做振动分析。满载时要模拟货物，压载时要模拟压载水。一般原则上采用集中质量单元或者实体单元来模拟这部分质量。本例全部采用实体单元来模拟货物和压载水质量。另外，本文还在水密边界采用集中质量单元来模拟燃油、淡水等物资。

附连水质量是振动计算中不能忽视的一个要素。目前，通常采用基于Lewis经验公式的三维势流理论或者基于流固耦合分析的源汇分布法进行计算。本文采取了后者以使计算尽量精确。MSC/NASTRAN通过运用Helmholtz源汇分布方法来求解Laplace方程［3］。该法将流体的作用和结构物的振动视为在流固耦合边界面上具有分布的脉动源，并离散成有限个源点。每个源针对不同方程产生一个简单解，将其整合就可以得到源强分布的线形方程矩阵。源强的值决定了分布源所产生的速度势和有效压力，进而可以反推出质量矩阵，得到附连水质量的准确分布。本例运用该法通过定义湿表面单元和吃水高度，并且将首尾吃水纵倾一并考虑分别准确定义了两种载况的附连水质量求解条件。

3 主要激励

准确的载荷施加对于振动计算结果起了决定性作用。船体振动激励主要有螺旋桨、主机和海浪。螺旋桨激励分为轴承力、舵力和表面脉动压力；主机激励分为1、2阶不平衡力矩，H、X、L型激励；海浪则有弹振和拍振激励。常规上来说最主要激励源是螺旋桨对船体叶频和倍叶频表面脉动压力；主机的2阶不平衡力矩，H，X型激励，其他激励与之相比过小，可以忽略不计。本次计算采用这些常规激励。当然，400000 DWT矿砂船的特殊性在于船体过大，总振动频率过低，故有可能在海浪激励下发生较大的振动。这方面已经通过在挪威进行弹振和拍振试验获得验证。该课题不在本文讨论范围之内。

3.1 螺旋桨激励

螺旋桨诱导的对船体尾部的表面脉动压力是船体振动最主要的激励源之一。表面压力由非空泡螺旋桨和空泡螺旋桨产生压力合成而得出。目前一般采用经验公式、模型实验和CFD理论计算。经验公式经济简便，但准确度不是太高；模型实验虽然准确，但只可能得到船尾脉动压力峰值，而如果要得到压力分布需要测点太多，实际操作是不现实的；CFD理论计算结果相对准确，但是成本高昂，而且空泡汽化破裂过程是非常难以模拟的，即使是CFD计算也需要结合模型实验不断调整参数，工程运用上该方法代价太大，除非潜艇、豪华邮轮等特种船舶，否则不适合推广运用。

本次计算采用结合模型试验修正Holden回归经验公式法来计算螺旋桨脉动压力。作为目前最为广泛应用的经验公式，Holden法是DNV于1979年在72条实船上总结出的回归经验公式［4］。该法操作简便，能够分别模拟空泡螺旋桨和非空泡螺旋桨产生的脉动压力并将其合成，并且压力作用范围波及全船湿表面，不像绝大多数类似经验公式只能模拟出螺旋桨上方D×D范围内压力，计算结果相对准确，非常适合有限元加载。本文还结合了MARINTEC水池模型实验，修正了该公式的几项重要伴流参数，使得螺旋桨上方脉动压力和实验结果接近并留有一定的安全余量。本文对PATRAN运用PCL进行二次开发，成功实现了Holden法的加载。图3、图4分别给出满载时叶频和倍叶频在最大工作转速的压力分布。压载情况类似，限于篇幅所限，这里就不给出了。

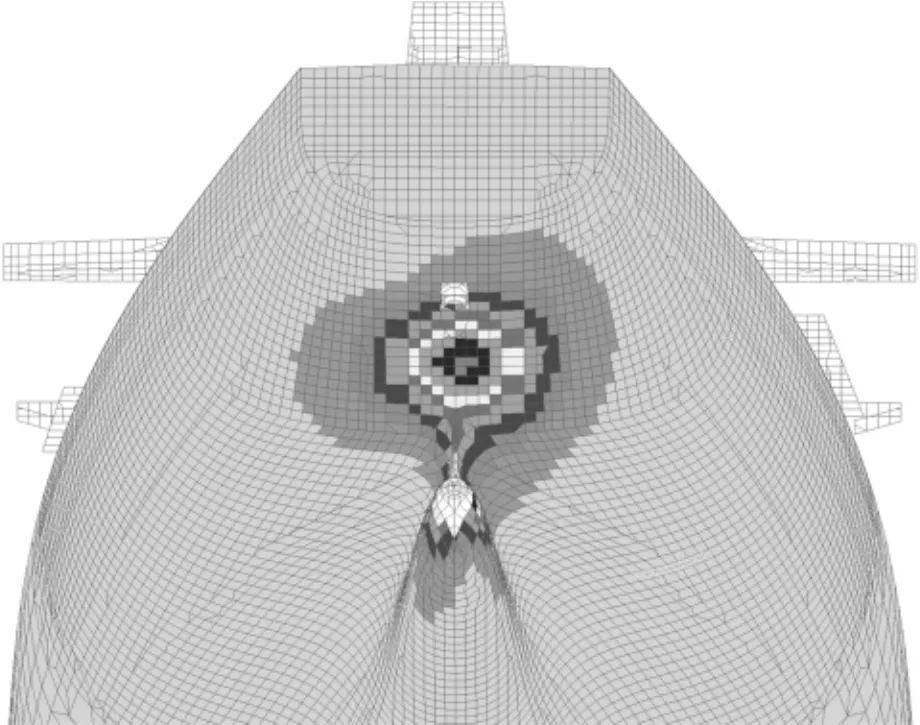
图3 满载最大工作转速下叶频脉动压力分布

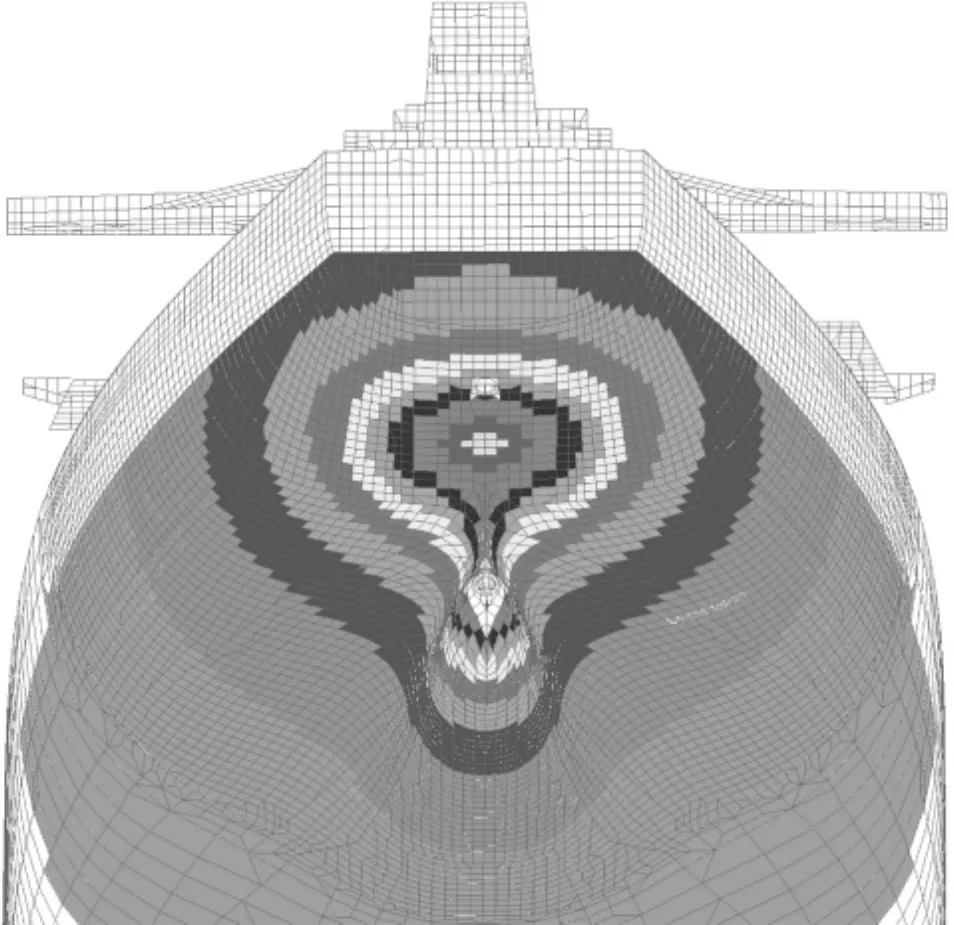
图4 满载最大工作转速下倍叶频脉动压力分布

图3、图4仅显示了最大工作转速下的脉动压力。根据类似船舶资料，在非最高转速下，螺旋桨激振力大小按照转速成3.5次方衰减［5］，即为：

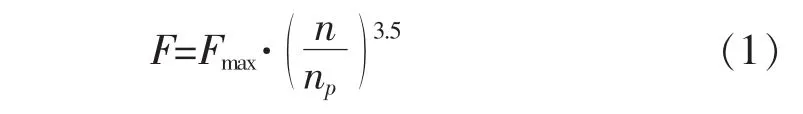
式中：np——MCR时的转速，Hz；

n——比MCR低的转速，Hz；

Fmax——MCR下的螺旋桨激振力，N；

F——转速等于N时的螺旋桨激振力，N。

3.2 主机激励

本船采用了WARTSILA的二冲程7缸主机SULZER 7RT-flex82T。查主机规格书，较有可能引起船体振动的激励有2阶不平衡力矩，7阶H型外力力矩，4阶X型内力力矩。具体数据如表1所示。

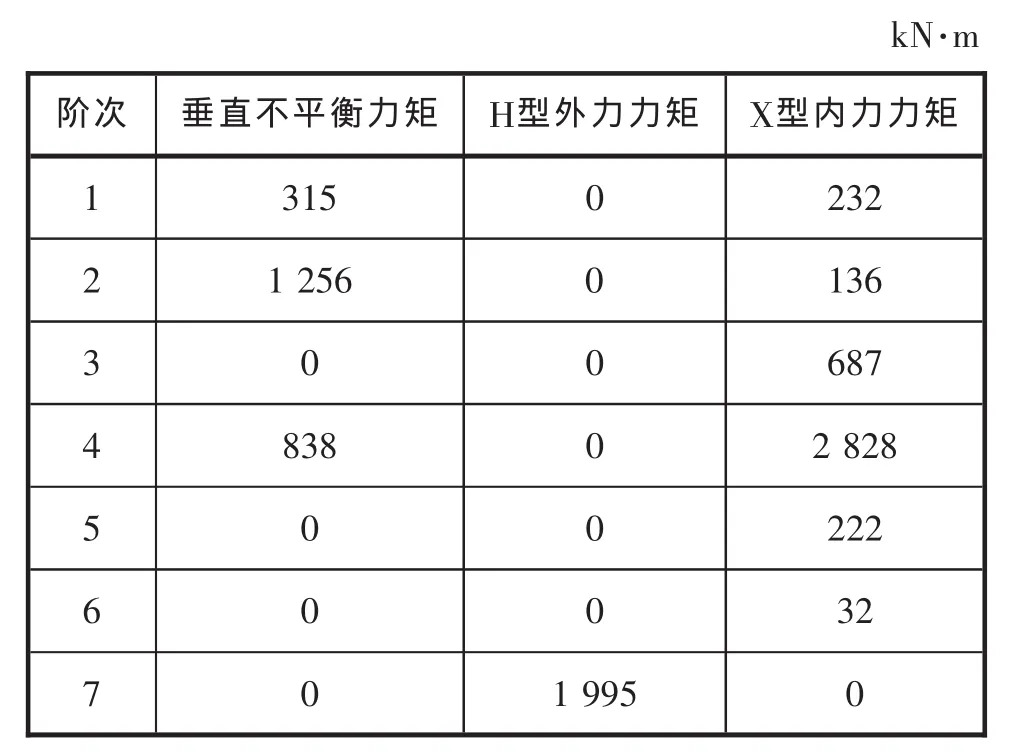
表1 SULZER 7RT-flex82T型主机各阶激振力矩

表1表征的是主机最大工作转速下的激振力矩。在非工作转速下，力矩值大小按照主机频率成平方衰减［6］，即为：

式中：np——MCR时的转速，Hz；

n——比MCR低的转速，Hz；

Mmax——MCR下的主机激振力矩，kN·m；

M——转速等于N时的主机激振力矩，kN·m。

4 振动计算方法的关键点

4.1 整船振动评估

一般整船振动的评估是首先计算整船的固有频率，然后与主要的激励频率对比，看该频率是否能避开主要的激励频率。由于本船吨位很大，前几阶固有频率肯定非常低，所以不可能发生因螺旋桨和主机激励引起的全船总振动。这里主要考察海浪为激励源的总振动评估。前文已反复提及，这里不再赘述。

4.2 局部振动评估

因为已经有了精确的整船振动模型，所以本例可以采用精确的子结构界面位移综合法（又称静态凝聚法）来得到任意局部结构的边界条件，进而得到准确的局部结构固有频率，最后就能评估该结构的振动特性了。该方法的原理简要说明如下：

NASTRAN中规定f-集为结构中“自由”的自由度，即除去多点和单点约束后的全部节点自由度；a-集为求解实特征值的分析集合。o-集为通过静态凝聚技术省略掉的节点自由度集合，所谓静态凝聚技术就是将f-集减缩成o-集和a-集。表达为f-seto-set=a-set［1］。 现举例如下：

设想有两个部件，分别是部件1和部件2。两部件在界面1-2上连接。令界面的位移自由度为{u}1-2，它的节点自由度为两部件共有。每个部件的f-集位移可以表达为

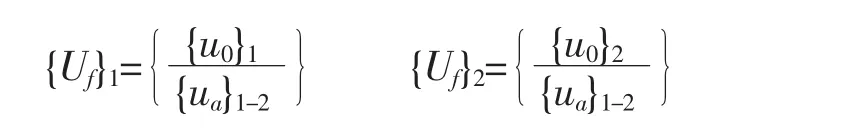
通过静态凝聚，可以将每个部件减缩到只有界面自由度集。设置［K］为刚度矩阵，{P}为载荷矩阵，则两个减缩方程为

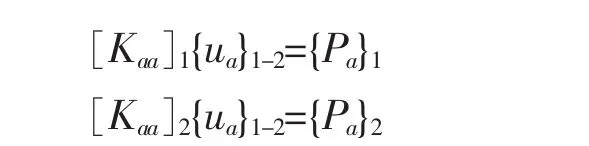
由于两个方程是对于同一组位移的，位移坐标系也一致，在将刚度和载荷相加后得到

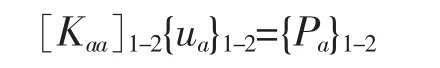
在求解界面位移后，就可以计算每个部件的内部位移，然后进而计算所需要的物理变量。本例中应用该方法可以很方便地计算局部构件固有频率。

4.3 阻尼

阻尼在自由振动计算中没有用处，在时域响应计算中作用有限，但是在本文的频域响应计算中却有着非常重要的作用。众所周知，稳态振动特性中，振幅取决于力学品质因数Q。该值越大，则共振时产生的振幅越剧烈。根据公式：

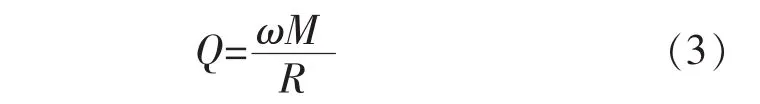
式中：ω——圆频率；

M——振动参与质量；

R——阻尼。

我们可以得出结论：在结构固有频率和振型都得到确认的情况下，共振时产生的响应幅度将完全取决于阻尼和激振力的大小；而且阻尼越小，振动越剧烈［7］。

阻尼可视为黏性阻尼、结构阻尼和摩擦阻尼的合成。其中占主导因素的结构阻尼机制至今还不清楚，难以量化；黏性阻尼可以通过水动力分析得到；摩擦阻尼在动力学分析中一般不考虑［8］。因为阻尼值目前还不可能数值化计算，所以一般都采用经验所得的临界阻尼值来设置。真实的临界阻尼值是随着频率的升高而增大，不同船级社有不同的阻尼的推荐值。因为是首制船，在比较分析了几家船级社的推荐值后，本文选取了最偏于安全的ABS推荐的恒定临界阻尼值 1.5%［9］。

5 计算结果分析和结构改进

5.1 总振动固有频率计算

由于模型巨大，所以采用了模态综合法而非直接法进行了计算，得到了满载和压载下的各11阶基础频率。表2给出了频率值和振型。

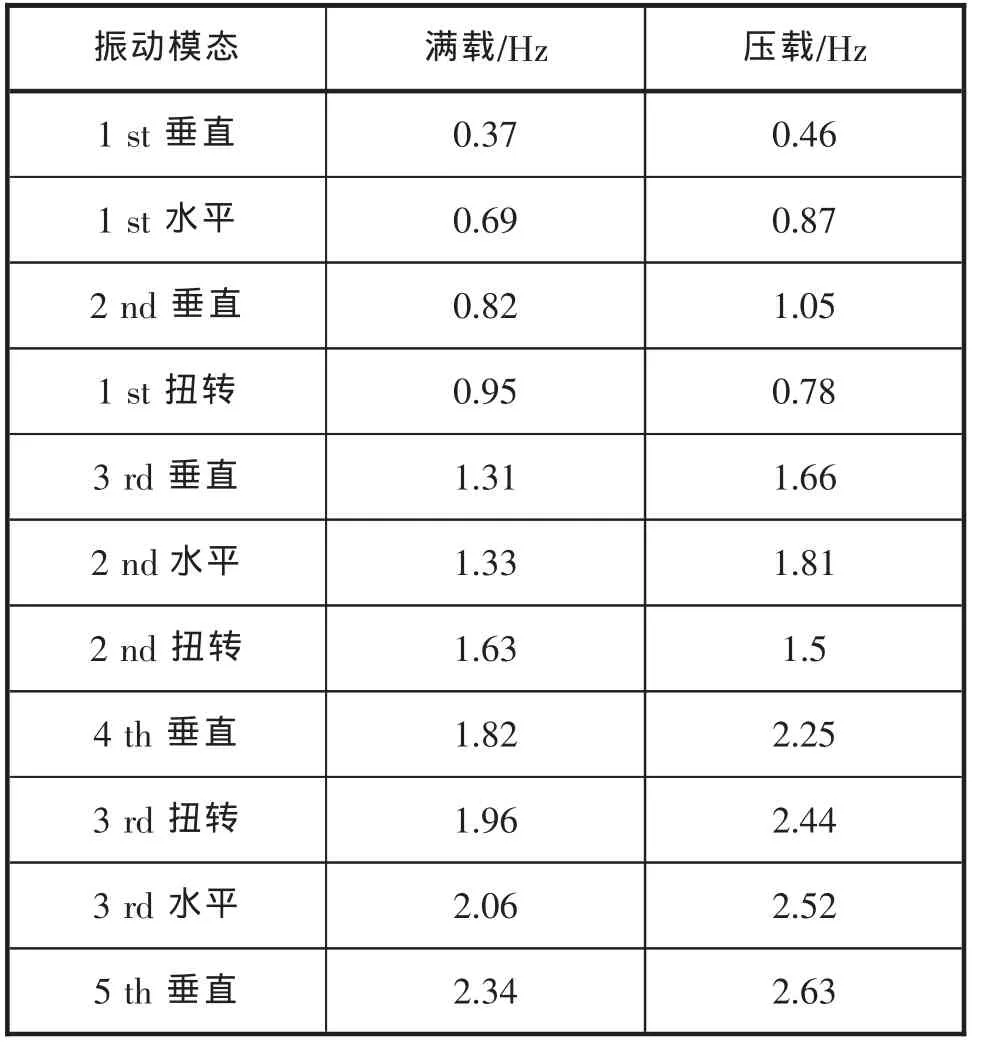
表2 总振动自由频率

其中，满载和压载的两节点（1阶）频率将用于弹振和拍振实验。频率和振型如图5、图6所示。

5.2 局部振动结果评估

在所有局部振动中，危害最大的就是上层建筑整体纵振，所以首先要计算上层建筑的固有频率，看是否高于螺旋桨叶频至少20%［10］。方法用前文所述的界面位移综合法。

图5 满载两节点自由频率0.37 Hz

图6 压载两节点自由频率0.46Hz

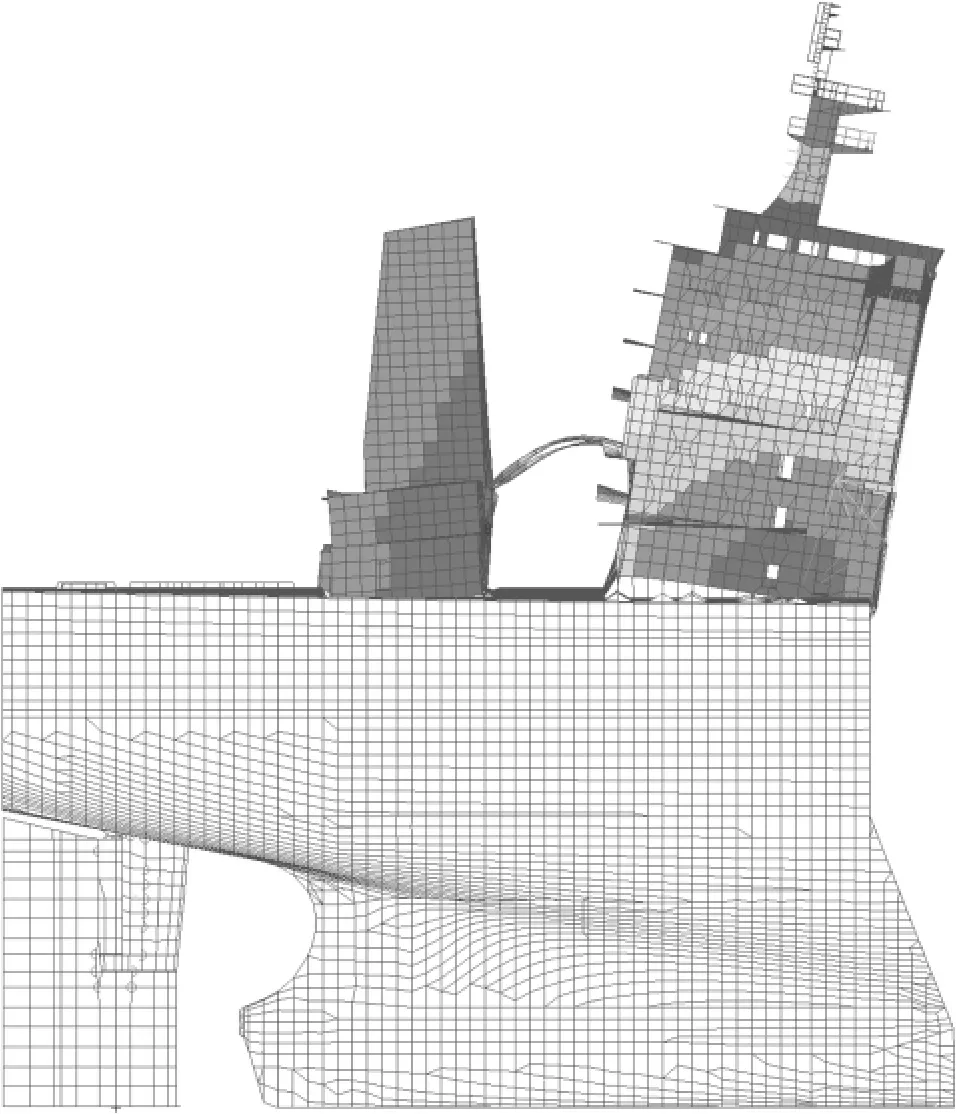
图7 上层建筑纵向振动频率9.2 Hz

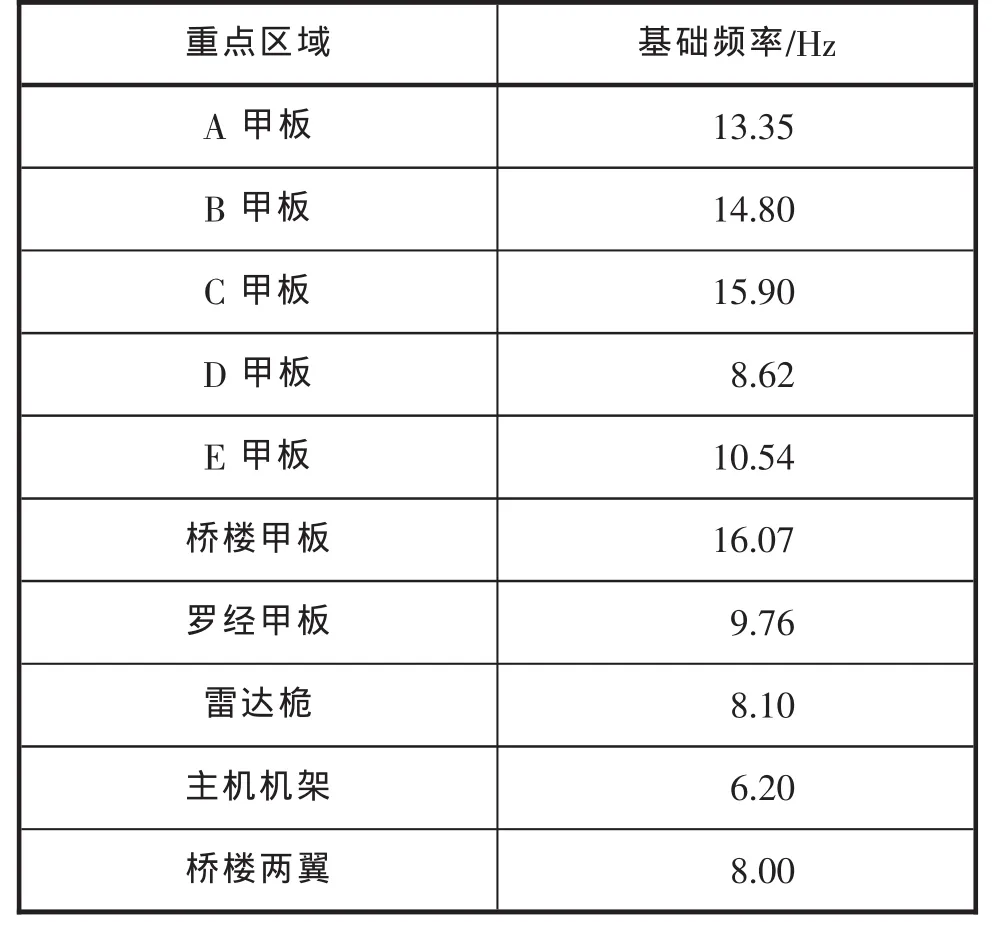
表3 船舶重点区域结构的基础频率

计算显示上层建筑纵向振动频率对螺旋桨叶频基本保有80%的设计余量，也就排除了其发生纵振的可能性。本文用类似方法分别计算出了上层建筑甲板和其他重点部位的基础频率。

按照GL要求［2］，局部结构固有频率必须对主机缸频或者螺旋桨倍叶频保持20%的余量。因为本船倍叶频激励太小可以忽略，所以局部结构原则上应该达到 1.2 倍的主机缸频以上，即 10.6 Hz，可以看出D甲板、罗经甲板、雷达桅、主机机架、桥楼两翼频率储备均不满足要求。雷达桅、主机机架、桥楼两翼频率更是落到了激励频率以内。这样就需要进行响应计算的进一步验证。

5.3 强迫响应计算评估

计算中发现螺旋桨引起的振动非常小，主机其他激振力也无大碍，但是H型激振力却引起了船体多处极为剧烈的振动。以下以满载载况为例说明这一情况，压载载况类似。

图8显示主机整体在6.2 Hz附近，整体发生剧烈的横向振动。横向速度响应最大达到了25.5 mm/s。

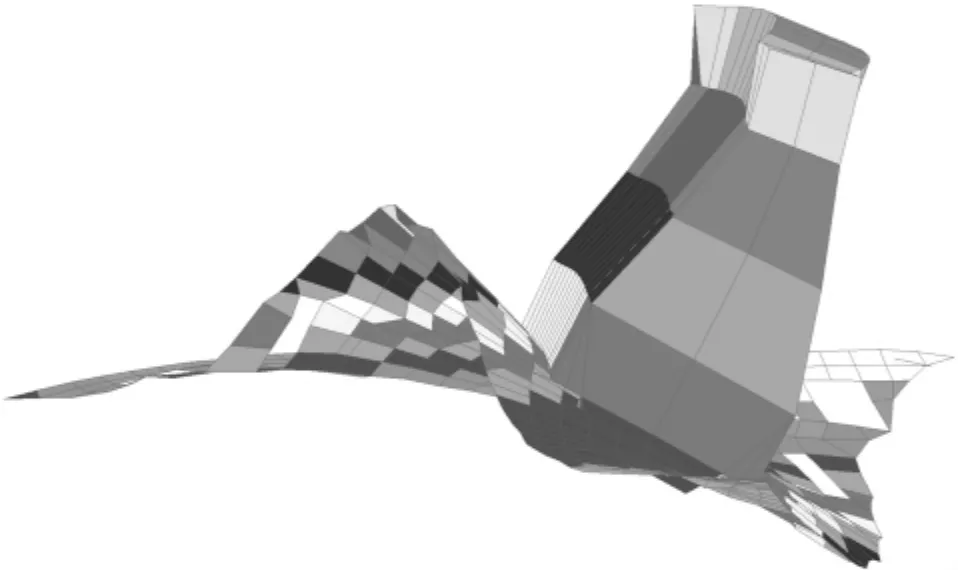
图8 主机机架在6.2 Hz时发生严重共振

图8显示共振频率和GL的振动指南的H型频率是几乎一致的 （GL指南上的7缸机无横撑H型振动频率是 5.9～6.5 Hz）［2］， 机舱顶部响应值和 CCS船上振动指南的响应值也几乎一致。CCS指南上的范例在没有横撑的情况下机舱顶部横向响应值是25 mm/s［11］。不仅如此，由于主机发生了严重的自振，

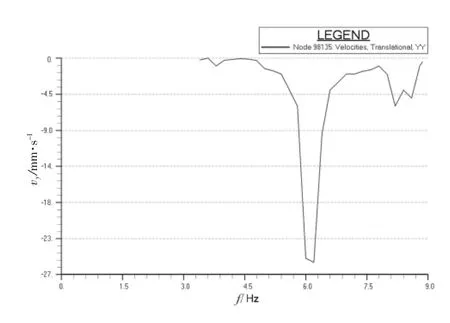
图9 机舱顶部一点横向速度响应曲线

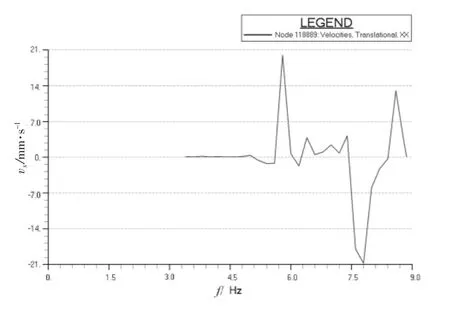
图10 桥楼甲板左舷翼顶部节点纵向速度响应曲线

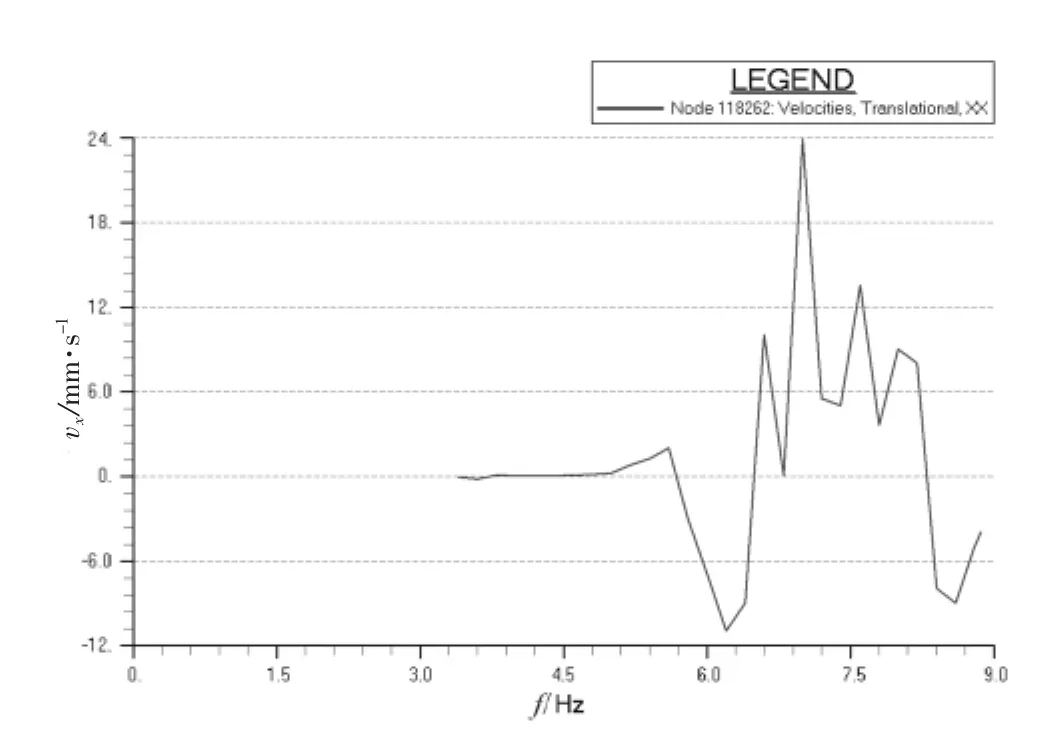
图11 桥楼甲板右舷翼顶部节点纵向速度响应曲线

图9～12中的速度响应极值分别达到了25、21、24、30 mm/s。基于H型激振力引起如此剧烈的振动，通过普通的结构修改可能无法满足振动要求，我们尝试在主机上添加横撑，用以提高主机的固有频率，避免主机和H型激振力共振，并且进一步避免主机自身振动所引起的2次振动源引发上层建筑振动。加横撑可以有3种方案，即左舷加、右舷加和双侧加。为验证最好的效果，本次计算对这3种方案都作了详细的分析对比。计算发现主机单侧（无论哪侧）加横撑，主机本身就可以完全满足振动要求，上层建筑大部分区域也将满足振动要求。但是考虑作为2次激励，引起了上层建筑多处剧烈振动。这里以最有典型意义的桥楼甲板两翼和雷达桅为例子，如图9～12所示。到本船主机质量过大，即使一点振动传递到上层建筑也会放大其效果，所以并不能完全消除振动影响。由于本船有一定特殊性，即两翼非常长且非常难以加强，所以无论哪侧加横撑都不能完全消除振动的恶劣影响，且右舷翼比左舷翼更加薄弱，横撑加在右舷主机本身振动会比左舷更强一些，所以右舷的振动条件更差一点。如果两侧都加横撑将基本消除主机的自身振动，并且上层建筑所有重点部位将满足振动要求，不需要再做大的结构改动。图13～16中的速度响应极值在主机双侧添加横撑后分别降到了0.65、4.50、7.00、3.00 mm/s，完全满足 ISO 6954 的振动衡准要求。

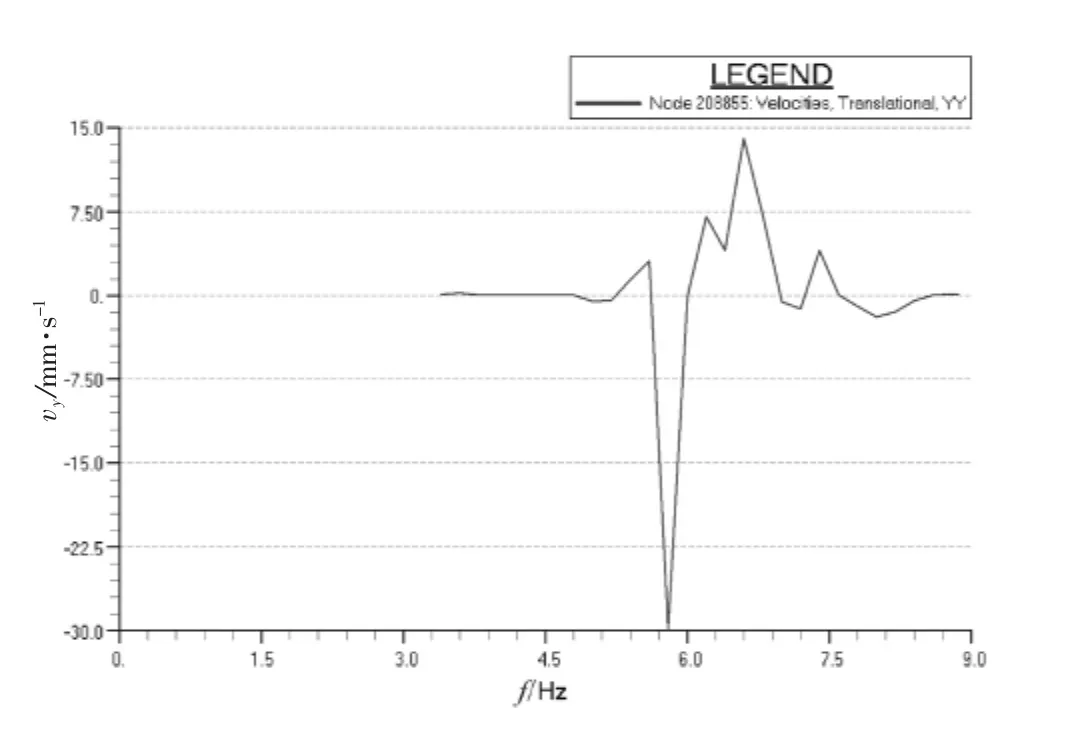
图12 雷达桅平台板上一点横向响应速度曲线

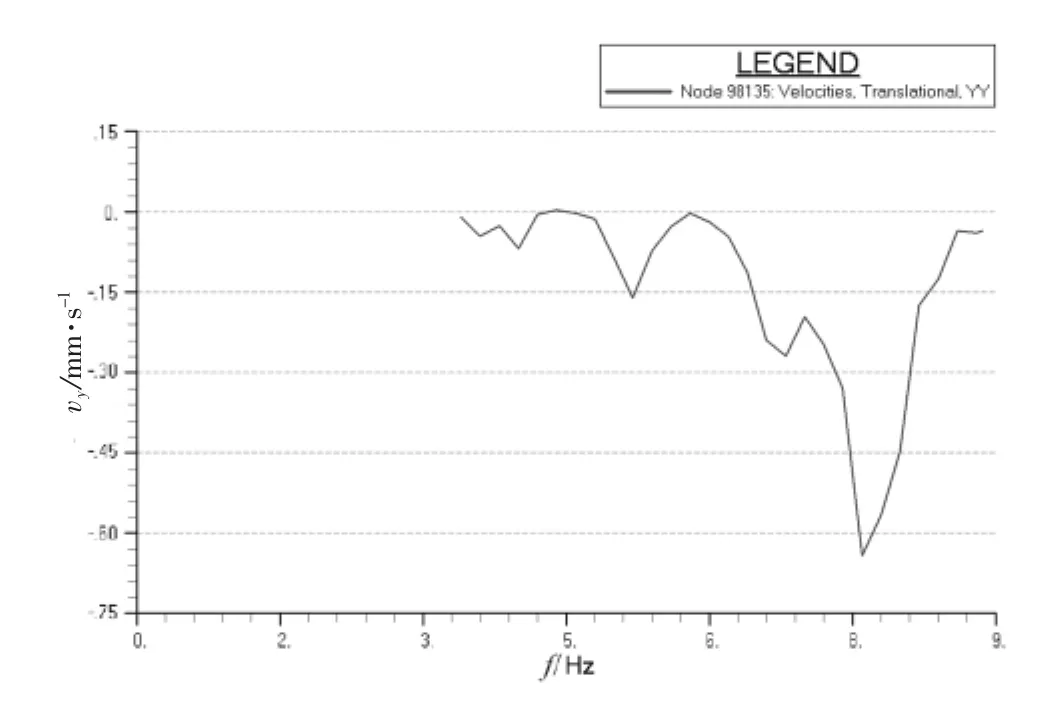
图13 机舱顶部一点横向速度响应曲线

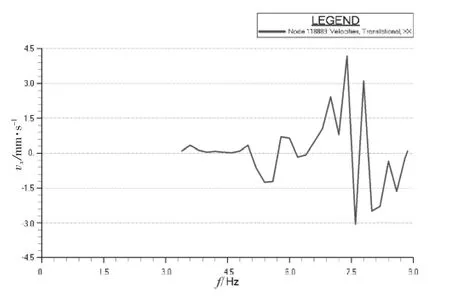
图14 桥楼甲板左舷翼顶部节点纵向速度响应曲线

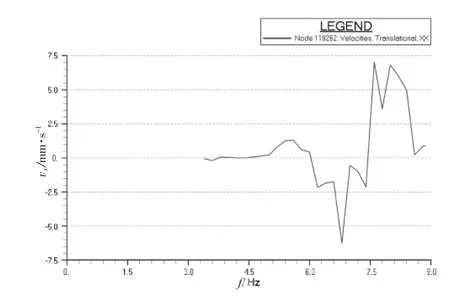
图15 桥楼甲板右舷翼顶部节点纵向速度响应曲线

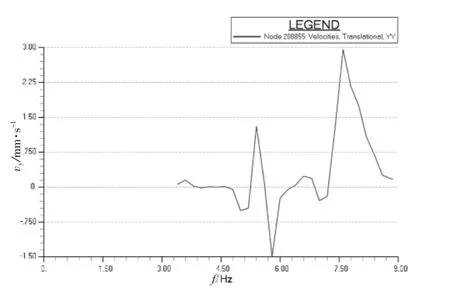
图16 雷达桅平台板上一点横向响应速度曲线

计算中还发现添加横撑的刚度和横撑所连接船体的刚度也非常关键。经过反复计算比较，最终确定横撑及其连接船体刚度都必须达到至少10e9 N/m才可以满足振动要求。如果该处构件不能满足所需的刚度要求，不仅不能减小振动，还有可能加剧振动［11］。目前有关主机添加横撑的方案和横撑刚度的要求已经得到了主机厂商的确认。

［1］MSC.MSC Nastran2003-Linear static analysis user’s guide［M］.Tokyo，2003.

［2］Iwer Asmnssen.Wolfgang Menzel.Holger Mumm.Ship Vibration［M］.Germanischer Lioyd.Hamburg，2001.

［3］MSC，MSC Nastran Version 70-Advanced dynamic analysis user’s guide ［M］.Tokyo，2003.

［4］Holden.K.O et.al Excitation forces and afterbody vibrations induced by marine propeller blade cavitation ［R］.Oslo:Det norske Veritas，1979.

［5］Prevention of harmful vibration in ships ［M］.Det norske Veritas Oslo.1983.

［6］Germanicher Lloyd Global Vibration Analysis of 2750 TEU Container Vessel［M］.2006.

［7］杜功焕，朱哲民，龚秀芬.声学基础［M］.南京：南京大学出版社，2009.

［8］姚熊亮.舰船结构振动冲击与噪声［M］.北京：国防工业出版社，2007.

［9］American Bereau of Shipping，Guide notes on ship vibration［M］.Houston:ABS Plaza，2006.

［10］O.M.帕利著.船舶结构力学手册［M］.徐秉汉译.北京：国防工业出版社，2002.

［11］中国船级社.船上振动控制指南［M］.北京，2000.