两正态总体均值与标差商的比的似然比检验ALI AL-SHAMI

（安徽师范大学数学计算机科学学院，安徽 芜湖 241003）

两正态总体均值与标差商的比的似然比检验ALI AL-SHAMI

（安徽师范大学数学计算机科学学院，安徽 芜湖 241003）

两个正态总体的均值与标准差的商的比值等于定值的似然比检验.给出了假设下的最大似然估计,似然比统计量及其渐近分布。

正态总体;最大似然估计;似然比检验

主要结果

考虑检验问题：

这里K是某个已知常数.

似然函数为

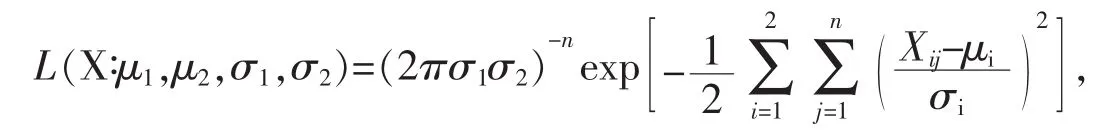
在Θ1中，μi，σi，i=1，2的MLE分别是其中

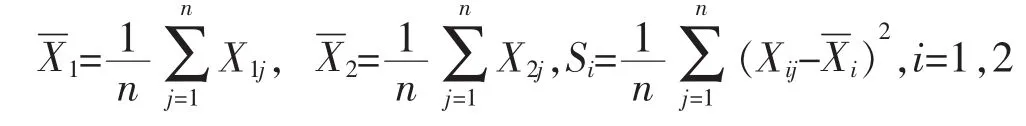
在零假设下，σ1，σ2和t的MLE由定理1给出.

定理1：在H0下σ1，σ2和t的MLE分别是.

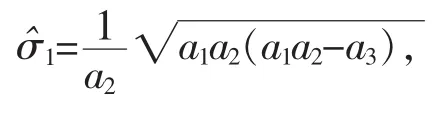
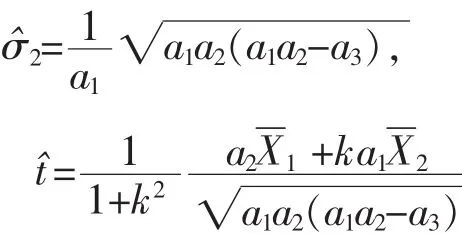
证明：

此时的似然函数为

对（2）式两边关于参数求偏导并令其为零得到

由（5）得

将（6）式代入（3）式得

将（6）式代入（4）式得

经整理，（7）式变为

（8）式变为

将（10）式代入（9）式得

整理得

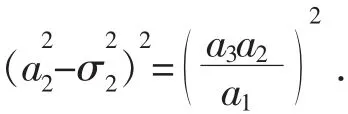
由（10）式知a3与同号，故

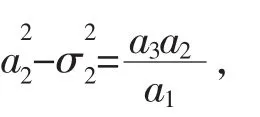
从而

将（11），（12）两式代入（6）式得

定理2：对检验问题H的似然比检验的统计量是

当H0立时，-2logT的渐近分布是自由度为1的χ2分布.

将定理（1）中得到的H0下的σ1，σ2和t的MLE代入（1）得

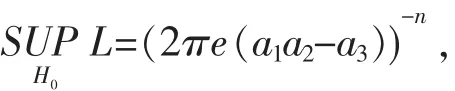
故似然比统计量为

当T≤C时拒绝H0.由Wilks[3]可知-2logT的渐近分布是自由度为1的χ2-分布.

[1]冶金工业部沈阳勘察研究院.锦州市安居工程秋B小区岩土工程技术报告[R].1997.

[2]锦州市岩土工程开发测试中心.安居工程秋B小区地基检测技术报告[R].1997.

[3]锦州市民用建筑设计研究院.安居工程秋B小区地质勘察报告[R].1997.

[4]GBJ79-91.地基处理技术规范[S].

[5]Yo un-Min Chou and Owen,D.B.A Likelihood Ratio Test for the Equality of Pro po rt ions of Two Normal Populat ions.

[6]Comm.Statist.1991,20（8）.2357-2374.

[7]Lohrding R K.A Test of Equality of Two Normal Population Means Assuming Homogeneous Coefficients o f Variation[J] Ann.Math.Statist.1969,40（4）.1374-1385.

[8]Wilks S S.Mathematical Statistics[M].Wiley,New York.1963.

[9]Miller E G.and Karson M J.Testing Equality of Two Coefficients of Variation[M].ASA Proceedings of Business and Economic Statistics Section.1997.278-283.

[10]Gray bill F A.Theo ry and Applications of the Linear Model[M].M assachusetts:Dux bur y Press,1976

责任编辑：陈 侃

O212.3< class="emphasis_bold">文献标识符：

符：A

1672－2868（2011）03－0022－03

2011-3-28

ALI AL-SHAMI（1977-），男，也门人。安徽师范大学研究生，研究方向：多元统计及其应用