中子星性质的研究
2011-09-19孙建新
孙建新
(1.山西大同大学煤炭工程学院,山西大同 037003;2.山西大学理论物理研究所,山西太原 030006)
中子星性质的研究
孙建新1,2
(1.山西大同大学煤炭工程学院,山西大同 037003;2.山西大学理论物理研究所,山西太原 030006)
对中子星状态方程作了简介,对核物质能量密度的计算的近似方法作了说明。以此为基础,研究了相互能对总能量的贡献,把相互能引入计算中,得到中子星质量、半径及密度的关系。
中子星;核物质;能量密度
众所周知,中子星是一个有着极端属性的致密星球[1],它的中心密度可达到约1017g/cm3,磁场强度可达到约1015G,角速度可达到约103s-1。在超新星爆炸期间质子中子星引力能的绝大部分被带走,中微子在巨大星体演化的最后阶段扮演着重要的角色。核物质计算在天体核物理和粒子物理领域的计算是非常广泛的。特别是在中子星上的应用[2],它是和超新星爆炸剩余物相联系的,比较著名的有巨蟹星座。典型的中子星质量M*大约是太阳质量Ms的1~2倍,半径大约是10km,中心密度约是1017g/cm3。在这样高的密度下,中子星内部是没有原子结构的,它是中子和小部分的质子与电子构成的核物质。基于近期对中子星的研究[3],进一步了解到对一个球对称体,它的引力场是非常强的,其张力被Schwarzschild解定义。它的压力和质量沿半径的分布服从Oppenheimer-Volkoff方程[4]:

初始条件M(0)=0和边界条件P(r*)=0确定中子星外半径r*。因此,可以通过质量半径关系M*=M(r*)算的中子星的总质量。结果依赖于中心密度ε(0)=ε*和状态方程。
1 研究方法
中子星核物质是介于P=ε和服从一般指数关系P=εα的费米气体之间的一种物质,在零温时的能量密度为:
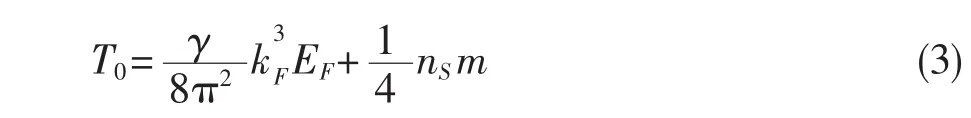
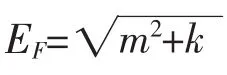
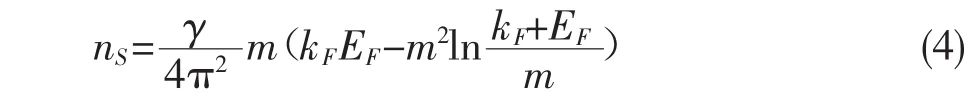
其中,nS是标量密度。对称核物质的简并系数γ=4(纯中子物质γ=2)。考虑到核物质粒子间相互作用引起的能量密度项W,整个系统的能量密度可写为:

压缩模数K和每个核子的束缚能E=ε/n的关系是:
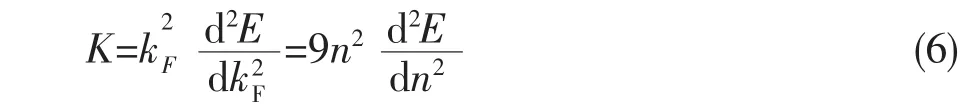
能量函数ε[n]和E[n]对理解压力P=-n(2dE/dn)是相同的。把压力P=-n(2dE/dn)和ρ=mn代入方程(1)和(2)中可得到中子星参数。较强的相互作用暗示了状态方程是硬的,这对巨大的中子星是可以理解的。现代研究估计中子星最大质量大约是太阳质量的1.5到3倍,不确定性反映了高密物质的状态方程不能精确地知道,并且中子星的质量对状态方程参数的改变是非常明显的。
科学研究者从来没有停止对相互作用项作更好的近似的研究,并进而得到更切合实际的核物质状态方程。对很多计算,相互作用是通过Hartree项作近似的,更复杂的Hartree-Fock[5]近似是估计了附加交换贡献项Wx,很多计算截止到了这一项。然而,精确的计算应包括相互能Wc的贡献,即:相互能的估计总是非常复杂的,在实际的核物质粒子的研究中总是被忽略掉。用σ-ω模型非线性方法描述介子场是非常复杂的,这个计算需要更多的努力,并且在随机项近似下计算,但也只能估计总相互能的40%。还有一个问题是大量的σ介子会导致核子质量的改变,因此,应该考虑对结果的修正。

我们用确切的状态方程来找出中子星参数是非常可取的,相互能的本质得到体现。关于相互能的确切描述是用拉氏密度函数计算σ模型的:
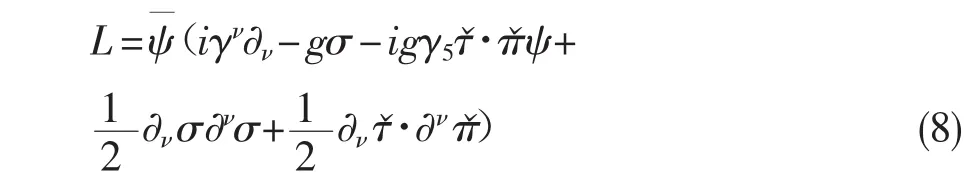
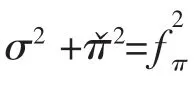

扩展的交换能Wx是两项的总和:
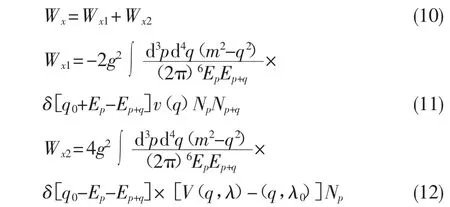
其中,
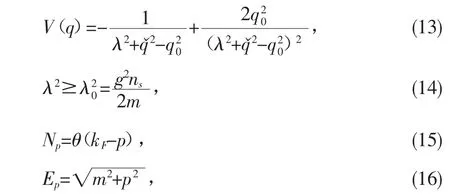
其中,参数λ是自洽的。并且有关系式:
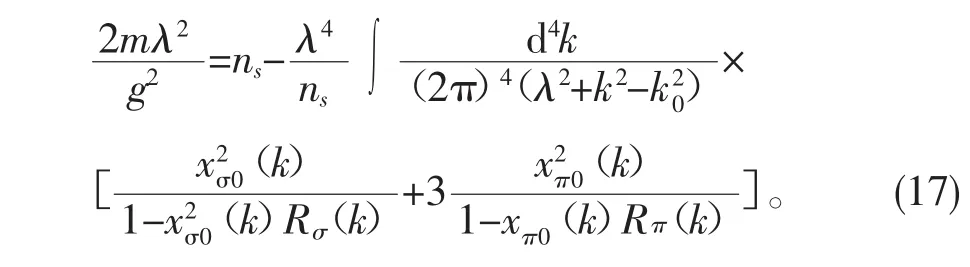
其中,xσ0和xπ0是σ介子和π介子非相互作用函数,并且

相互能可表达为:

有上述式(18)~(23)可确定相互能的值。系统总的能量密度也可有上述诸式确定,所以,可以得到每个核子的束缚能E=ε/n。
如果调整耦合常数g=13.96,得到以实验为依据的饱和值EB=-15.75MeV,对应的费米动量和压缩模数分别是kF=1.39fm-1和K=285 MeV。在理论上原则上可以预言的变化范围在110~470MeV。同样计算了没有相互能贡献的状态方程,这个近似的精确度是接近对应的Hartree-Fock水平的。
2 结果及讨论
通过模拟Oppenheimer-Volkoff方程(1)和(2),得到图1和图2。图1描绘了中子星质量M*(以太阳质量为单位)和中心密度ρ*(以ρ0=2.8×1017g/cm3为单位)的关系。实线代表包含相互能的状态方程,虚线代表不包含相互能的状态方程。图2描绘了中子星质量M*和半径r*的关系。实线与虚线表示的含义与图1相同。从图中可看出,在考虑了相互能时,最大质量是1.64Ms,对应的中心密度是7.87ρ0(ρ0=2.8×1017g/cm3是标准密度),半径是9.82km。如果应用现在的计算到Crab脉冲星中,因它的质量M*=1.44Ms,我们能估计它的半径约是10.8km,中心密度约是5.2ρ0。Hartree-Fock近似预言了中子星最大质量M*=2.06Ms,半径r*=12.07km,中心密度ρ*=6.79ρ0总的来说,质量和半径的关系是非常密切的,当半径有小的变化,质量的变化也是很明显的。
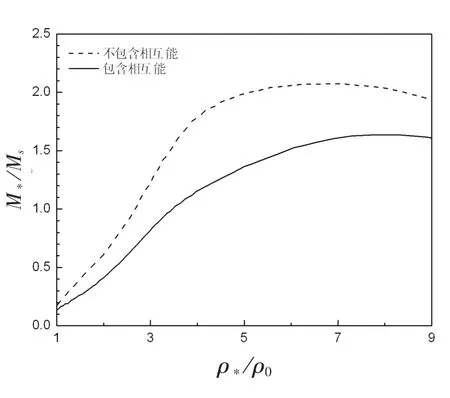
图1 中子星质量(以太阳质量为单位)与中心密度的关系(以ρ0=2.8×1017g/cm3为单位)
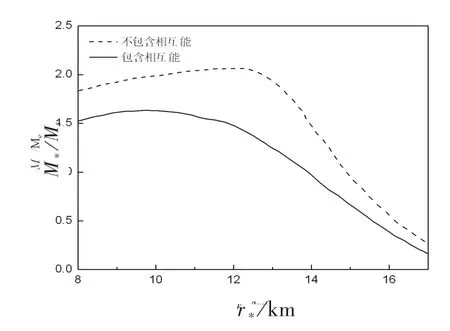
图2 中子星质量与半径的关系
我们的结果在早期研究讨论的值的范围内,核物质可以有非常软的状态方程,对应的压缩模量K=225Mev,最大质量M*=1.45Ms。硬的状态方程对应的压缩模量K=300Mev,最大质量M*=2.1Ms。我们用的拉氏密度方程对应的是中间状态(K=285Mev和M*=1.64Ms)。然而,考虑到扩展函数项的优点和估计相互能,对软化状态方程的固态物体是非常好的,在核物质计算方面得到检验。Hartree-Fock近似过高的估计了中子星的质量,相互能的引入作了较大的修正[-(0.3~0.4)Ms]。更小心的估计是必要的,通过拉氏密度方程(8)描述了核物质,更多成熟的相互作用模型可以为我们带来更宽范围的取舍。但是,每一个特有的拉氏密度函数需要作特殊的分析,并且构造方程解。巨大的中子星有复杂的结构,包括奇异粒子(除了中子、质子和轻子)和夸克核心。然而我们仍然能推断出相互能的引入是正确的。它对在这个领域进一步研究提供了新的思想观念,有助于进一步明确中子星及其他天体潜在的核物理和粒子物理性质。
[1]潘娜娜.高密核物质动力学与中子星理论的观测限制研究[D].武汉:华中师范大学,2008.
[2]徐骏.非对称核物质热力学性质、中子星结构和蒙特卡罗算法相关问题的研究[D].上海:上海交通大学,2008.
[3]孙建新.关于中子星物质中的K介子凝聚[J].山西大同大学学报:自然科学版,2009,25(3):24-26.
[4]周丽娜.有限温下含YY相互作用的中子星物质[D].长春:吉林大学,2008.
[5]米爱军.中子星的状态方程和性质以及非对称核物质中的核子超流性[D].兰州:兰州大学,2008.
〔编辑 李海〕
A Study on the Properties of Neutron Star
SUN Jian-xin1,2
(1.School of Coal Engineering,Shanxi Datong University,Datong Shanxi,037003 2.Institute of Theoretical Physics,Shanxi University,Taiyuan Shanxi,030006)
In this paper,we have made a brief introduction to the equation of state of neutron star and the approximation method to calculate the energy density of nuclear matter.On this basis,we researched the contribution that the correlation energy had done to the total energy,and by introducing it into the calculation,we got the relation between the mass,radius and density of the neutron star.
neutron star;nuclear matter;energy density
O434.14
A
1674-0874(2011)02-0027-03
2010-09-28
孙建新(1979-),男,山西山阴人,在读硕士,助教,研究方向:粒子物理与原子核物理。
