具有两个时滞的SEIRS脉冲接种模型的周期解

仝耀华，薛亚魁，李录苹

（1.山西大同大学数学与计算机科学学院，山西大同 037009；2.中北大学理学院，山西太原 030051）

具有两个时滞的SEIRS脉冲接种模型的周期解

仝耀华1，2，薛亚魁2，李录苹1

（1.山西大同大学数学与计算机科学学院，山西大同 037009；2.中北大学理学院，山西太原 030051）

讨论了具有两个时滞的传染病脉冲接种模型，考虑了周期解的存在性和全局吸引性。

时滞；脉冲；周期解；全局吸引性

1 模型的建立

本文将考虑具有两个时滞的SEIRS脉冲接种模型［1-4］

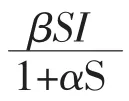
总人口N（t）=S（t）+E（t）+I（t）+R（t），

由系统（1）知

当t≠kT时，由系统（2）可以得到

μK-（μ+d）N（t）≤N（t）≤μK-μN（t）。

而N（kT+）=N（kT），

由常微分方程的比较定理可得

简化模型（1）得到

系统（3）的初始条件是

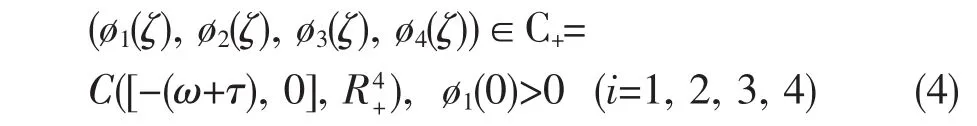
考虑实际生物意义仅在

2 周期解的全局吸引性

在这一部分中，首先讨论系统的周期解的存在性。此时系统（3）不存在染病者，即I（t）=0，t≥0。在这个条件下，易感者，恢复者，总人口应满足

得到下面关于系统（5）的极限系统

和

由文献［5］可知系统（7）的周期解为

定理2.1如果R*＜1，则系统（3）的周期解（Se（t），0，K-Se（t），K）是全局吸引的。其中

证明当R*＜1时，取一个充分小的ε0＞0，使得

由系统（3）的第一个方程，可得

S（t）≤（μ+γ）（K-S（t）。

考虑下面的比较系统

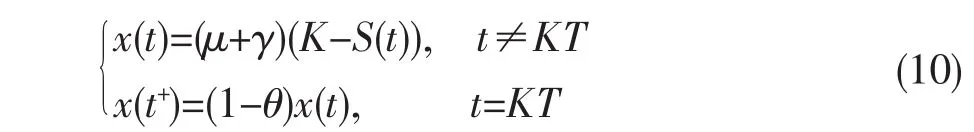
由文献［5］可知系统（10）的周期解

酸性解堵液加入胶塞中，在50～90℃条件下，1～4 h完全破胶，破胶液黏度低于5 m Pa·s，有利于从井筒排出。

xe（t）=K+（x*-K）e-（μ+γ）（t-kT），kT＜t≤（k+1）T。

是全局稳定的。其中

令（S（t），I（t），R（t），N（t）是系统（3）满足初始条件（4）和S（0+）=S0＞0的解，x（t）是系统（10）满足初始条件S（0+）=S0的解。

由文献［6］，［7］可知存在k1＞0，使得

S（t）＜x（t）＜xe（t），kT＜t≤（k+1）T，k＞k1。

也就是

由系统（3）的第二个方程，可以得到

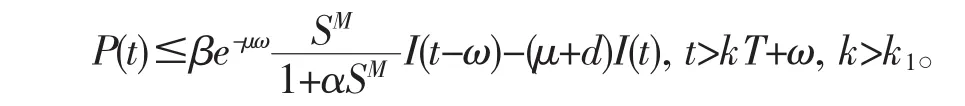
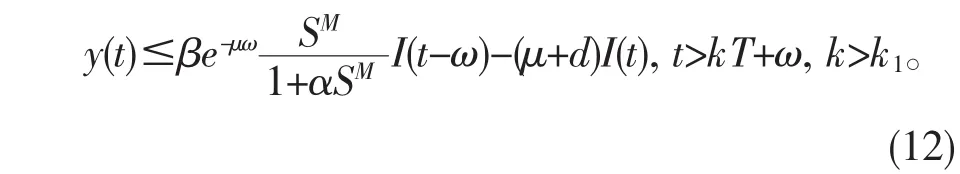
令（S（t），I（t），R（t），N（t）是系统（3）满足初始条件（4）和I（ζ）=φ（ζ）＞0（ζ∈［-ω，0］的解，y（t）是系统（12）满足初始条件y（ζ）=φ（ζ）＞0（ζ∈［-ω，0］的解。

由文献［6］，［7］，有

结合实际可知

因此对于充分小的ε1＞0，存在k2＞k1（k2T＞k1T+ω），使得对所有的t＞k2T，有I（t）＜ε1。

由系统（3）的第4个方程，可以得到

N（t）＞μ（K-N（t）-dε1，t＞k2T。

当t＞k2T时考虑下面比较方程

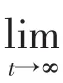
由（13）和（16）可得存在k4＞k3，使得

所以由系统（1）的第二个方程，可以得到

易知存在一个整数k5＞k4，使得

因此当t＞k5T时，由（17），（18）和系统（3）的第一个方程，可得

当t＞k5T且k＞k5时考虑下面比较系统

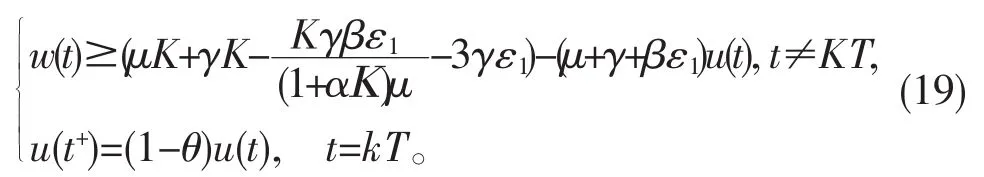
由文献［8］，得到（19）的周期解

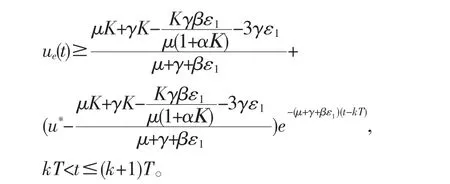
是全局稳定的。其中

由文献［6］，［7］可知存在k6＞k5，使得

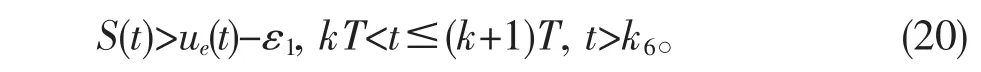
因为ε1充分小，由（11）和（20）可得

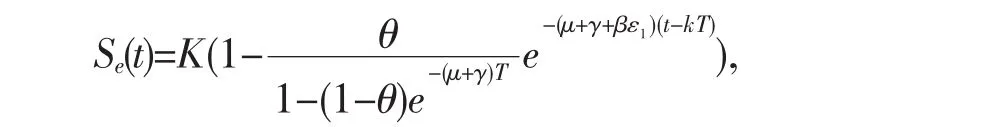
kT＜t≤（k+1）T是全局吸引的。也就是

又因为E（t）是正值且ε1充分小由（18）可知

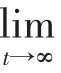
令

推论2.1（Ⅰ）如果Kβe-μω≤（1+αΚ）（μ+d），无病周期解（Se（t），0，K-Se（t），0）是全局吸引的。

（Ⅱ）如果Kβe-μω＞（1+αΚ）（μ+d），假如θ＞θ*或者T＜T*，无病周期解（Se（t），0，K-Se（t），0）是全局吸引的。

定理2.1描述了当R*＜1时，系统（3）的全局吸引性。

［1］Baino D D v，Simeonov P S.Impulsive differential equations：periodic solution and applications［M］.［s，l.］：Longman Harlow，1993.

［2］原三领，韩丽涛，马知恩.一类潜伏期和染病期均传染的流行病模型［J］.生物数学学报，2001，16（4）：392-398.

［3］薛亚奎，吴文利.一类次线性脉冲时滞微分系统的渐近性［J］.中北大学学报：自然科学版，2005，26（6）：391-395.

［4］Cull P.Global stability for population models［J］.Bull Math Biol，1981（43）：47-58.

［5］Onofrio A D.Stability properties of pulse vaccination strategy in SEIR epidemic model［J］.Math Biosci，2002（179）：57-72.

［6］Z Liu，R Yuan.Sstability and bifurcation in a harmonic oscillator with delays［J］.Choas Solitons and Fractals，2005（23）：551-562.

［7］Dong Y J，Zhou E X.An Application of coincidence degree continuation theorem in existence of solutions of impulsive differential equations［J］.Math Anal Appl，1996，197（1）：875-889.

［8］Kuang Y.Delay differential equations with applications in population dynamic［M］.New York：Acadermic Press，1993.

〔编辑 高海〕

Periodic Solution to SEIRS Pulse Inoculation Model with two Delays

TONG Yao-hua1，2，XUE Ya-kui2，LI Lu-ping1
（1.School of Mathematics and Computer Science，Shanxi Datong University，Datong Shanxi，037009；2.School of Science，North China University，Taiyuan Shanxi，030051）

This paper discussed the infectious disease model with two delays，considering the pulse inoculation periodic solutions of the existence and global exponential attract sexual

delay；pulse；periodic solution；global attract sexual

O175

A

1674-0874（2011）02-0011-03

2010-10-11

仝耀华（1979-），女，山西大同人，硕士，助教，研究方向：生物数学。