罗茨式三组元比例控制器的仿真研究
2011-09-19王育才
王 鹰, 王育才, 潘 光
罗茨式三组元比例控制器的仿真研究
王 鹰, 王育才, 潘 光
(西北工业大学航海学院, 陕西西安, 710072)
三组元比例控制器是水下热动力能源供应系统的关键组件, 其配比精度的高低, 对推进剂能效的发挥起着决定性的作用。对罗茨式比例控制器, 其比例控制精度主要受每路流体泄漏量的影响。通过对罗茨式三组元比例控制器的力学和泄漏量分析, 建立了罗茨比例控制器的数学模型, 在MATLAB环境下, 对其工作过程进行了数值仿真, 获得了诸如面积利用系数、定子内径、叶轮总高度以及端面间隙等重要参数的变化规律, 并分析了这些参数变化对比例(控制)精度的影响, 为其研制提供了理论依据。
罗茨式三组元比例控制器; 力矩; 泄漏量; 比例控制精度
0 引言
水下热动力系统使用的推进剂由燃烧剂、氧化剂和冷却剂三组元组成, 为充分发挥其能效, 对于三组元的配比比例有严格的要求。由于该产品的使用场所特殊, 国内外资料很难看到。
罗茨式三组元比例控制器的工作原理接近罗茨流量计, 它由3套类似于罗茨流量计的部件组成, 三路共轴同转速, 流量比例取决于三路的实际流量, 其比例精度主要由三路的泄漏量决定,而泄漏量由工作压差和间隙决定。
本文在对罗茨式三组元比例控制器进行力学和泄漏量分析的基础上, 建立其数学模型, 并利用MATLAB对其工作过程进行数字仿真, 获得了重要参数变化对比例控制精度的影响, 为其研制提供了参考。
1 数学建模
1.1 结构形式
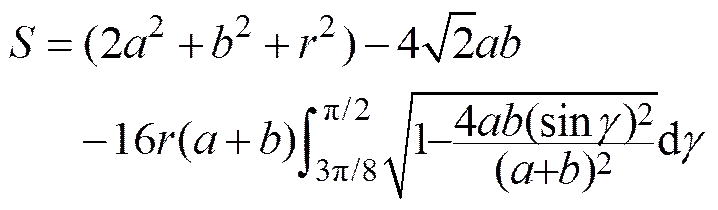
式中
(2)

(4)
文中下标=7,和分别表示燃烧剂、氧化剂和冷却剂, 设三路叶轮总高度为, 以表示单路的体积流量比重, 则每路叶轮的高度
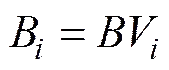
1.2 工作压差
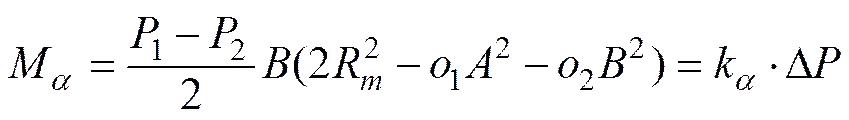
(7)
为防止流体向壳体外泄漏, 在轴两端分别放置大O型圈各一个, 小O型圈各2个, 其产生的摩擦阻力矩为
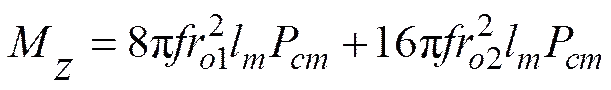
叶轮端面处的摩擦阻力矩总和为

两叶轮间以及叶轮与定子径向间的摩擦阻力矩约为端面处摩擦阻力矩的倍。由

可得工作压差为
(11)
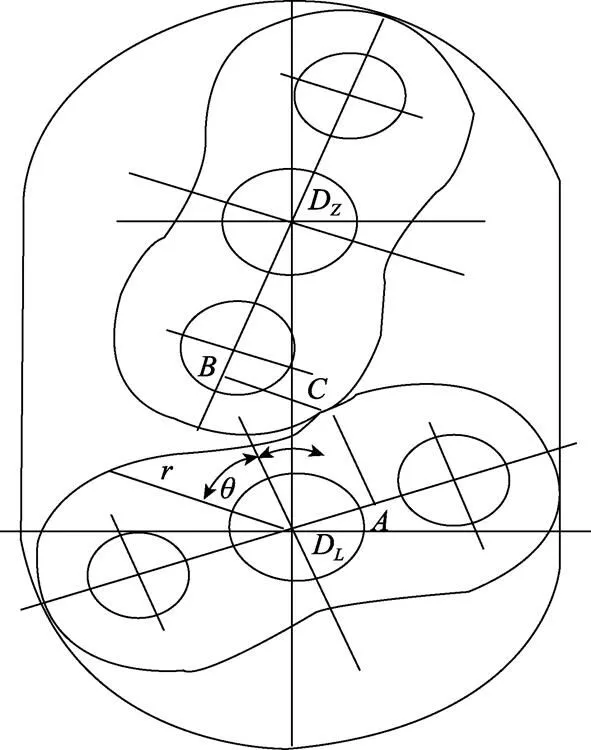
图2 比例器工作原理简图
1.3 泄漏量
由于叶轮结构对称, 所以由剪切流引起的泄漏量相互抵消, 只需考虑由压差引起的泄漏量。

(13)
由此可得叶轮端面处由压差引起的泄漏量为

叶轮径向顶端与定子间的压差流可视作孔口出流, 其湿周直径为
(15)

(17)
由此可得每路的泄漏量
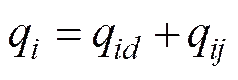
1.4 比例精度
由以上分析可知, 比例器单路的实际流量为

氧化剂和冷却剂与燃烧剂的实际体积流量比分别为
(20)

其理论体积流量比分别为
(22)
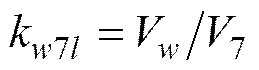
因此其比例精度分别为
目前洋山港已建一、二、三期集装箱码头,岸线总长5 640 m,其中一期工程共布置5个5万~10万吨级泊位,二期工程布置4个7万~10万吨级泊位,三期工程布置7个7万~15万吨级泊位。经加固升级改造,洋山港二、三期码头现可靠泊20万吨级集装箱船舶。[1]
(24)

2 结构参数对比例控制器性能的影响
通过前面的分析可知, 罗茨比例控制器的结构参数诸如面积利用系数, 定子内径, 叶轮总高度以及端面间隙对比例控制器的比例精度均有影响。下面运用MATLAB编程就这4个参数对比例控制器性能的影响进行数值仿真, 在分析某一参数对比例精度的影响时, 只改变所分析的参数大小, 其余3个参数均保持设计值不变, 同时工况均为最大流量。
2.1 面积利用系数对比例控制器性能的影响
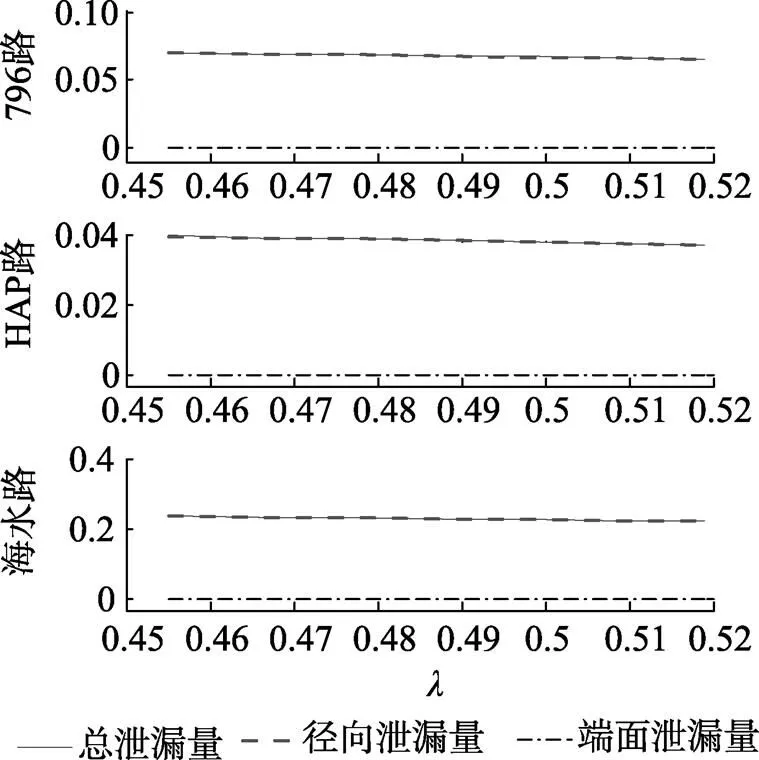
图3 泄漏量q与面积利用系数l的关系曲线

图4 每路比例精度与面积利用系数l的关系曲线
2.2 定子内径对比例控制器性能的影响

图5 泄漏量q与定子内径Rm的关系曲线
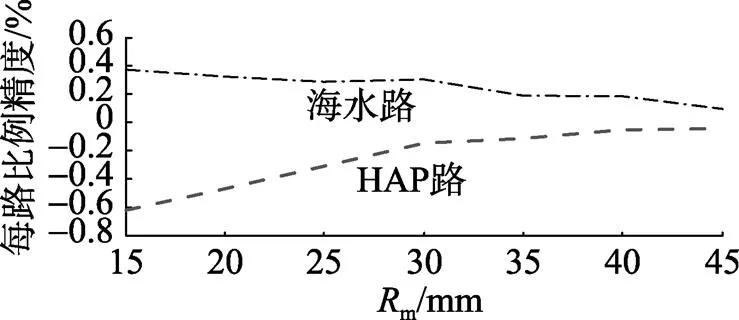
图6 每路比例精度与定子内径Rm的关系曲线
2.3 叶轮总高度对比例控制器性能的影响

图7 泄漏量q与叶轮总高度B的关系曲线
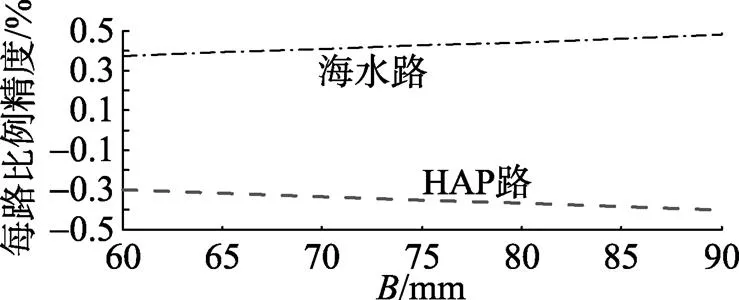
图8 每路比例精度与叶轮总高度B的关系曲线
在端面间隙很小的情况下, 整个比例控制器的泄漏量几乎全是由径向压差流引起的, 虽然的增大会使控制器的转速降低, 使控制器前后的工作压差降低, 但增大的同时使径向泄漏面积和径向泄漏量剧增, 这就使得由泄漏面积增大引起的泄漏量的增加远大于由压差减少带来的泄漏量的减少, 所以每路泄漏量增大, 比例精度降低。图7和图8的仿真曲线也证实了这一点。
2.4 端面间隙对比例控制器性能的影响

图9 泄漏量q与端面间隙dd的关系曲线

图10 每路比例精度与端面间隙dd的关系曲线
3 结论
改变定子内径、面积利用系数、叶轮总高度、叶轮与定子间的端面间隙对比例控制器的比例精度有着不同程度的影响。由前面的分析可知, 在罗茨比例控制器的设计中, 在空间许可的情况下, 应尽量增大其定子的内径和面积利用系数, 减小叶轮的总高度, 可以将端面间隙适当增加至0.03~0.04 mm。
以上结论提出了结构参数的正确选择原则, 从而为罗茨式比例控制器的设计和改进提供理论依据。
[1] 罗凯, 党建军, 王育才. 三路比例控制器比例精度分析[J].机床与液压, 2004(10): 139-140. Luo Kai, Dang Jian-jun, Wang Yu-cai. Proportion Precision Analysis of Tri-Proportion Controller[J]. Machine Tool & Hydraulics, 2004(10): 139-140.
[2] 刘金梅. 罗茨鼓风机叶轮CAD-CAM技术研究[D]. 长沙: 中南大学, 2007.
[3] 顾永泉. 流体动密封[M]. 北京: 中国石化出版社, 1992.
[4] 张也影. 流体力学[M]. 北京: 高等教育出版社, 1986.
[5] Smoldyrev A E.Calculation of Concentration and Velocity Distribution for Hydraulic Fluid Flow in Pipes[J]. Power Technology and Engineering (Formerly Hydrotechnical Construction), 2002, 36(4): 243-246.
[6] 魏学勤, 刘兴蓉. 腰轮流量计准确度的影响因素[J]. 机械研究与应用, 2005 (4): 46-47. Wei Xue-qin, Liu Xing-rong. Influence Factors on the Accuracy of Turbine Flowmeters[J]. Mechanical Research & Application, 2005 (4): 46-47.
(责任编辑: 陈 曦)
Simulation Research on Roots Tri-propellant Proportion Controller
WANG Ying, WANG Yu-cai, PAN Guang
(College of Marine Engineering of Northwestern Polytechnical University, Xi′an 710072, China)
Tri-propellant proportion controller is a key part of underwater heat engine energy supply system, its proportional precision is very important for exploiting the energy efficiency of the propellant. And for Roots tri-propellant proportion controller, its proportional control precision is mainly affected by the leakage volume of each way. In this paper, based on the analysis of mechanics and leakage volume of Roots tri-propellant proportion controller, a mathematical model is established, and numerical simulations are performed via MATLAB. Consequently, the variation rules of the important parameters, such as the utilization factor of area, the interior diameter of stator, the total height of impeller, and the end face clearance, are obtained. And the influences of these parameters on proportional precision are analyzed. This study may be applied to the development of Roots tri-propellant proportion controller.
Roots tri-propellant proportion controller; torque; leakage volume; proportion control precision
TJ630.32
A
1673-1948(2011)06-0463-05
2010-12-23;
2011-01-13.
王 鹰(1969-), 女, 硕士, 工程师, 研究方向为热能工程.
