形式幂级数环中的循环码

刘修生

（黄石理工学院 数理学院，湖北 黄石 435003）

1 引言

循环码是一类非常重要的码，首先是在二元域F2中研究循环码，然后扩充到有限域 Fq上( q = pr, p为素数， r ≥ 1 )。由于有限域 F 上长度为qn的循环码可以看成环 Fq[ x] xn- 1 的一个理想，在文献[1]中给出了这种域上循环码的构造。在文献[2]中，Norton 和 S alagean应用环同构技术扩充了文献[1]与文献[3]得到的定理推广到有限链环。接下来，Dinh和Lopez-permouth在文献[4]中用不同于文献[2]的方法研究了有限链环上循环码的生成元。近年来，Dougherty等研究了形式幂级数环R∞上循环码的投影码的循环性，得到了一系列的结果[5]。本文的目的是：由形式幂级数环R∞上码C投影码的循环性来研究码C的循环性，以及含有形式幂级环R∞的中国积中循环码来研究它的投影码的循环性。

2 有限链环与形式幂级数环

一个环R称为链环，如果它的所有理想在包含关系上是线性有序的，显然链环上的理想都是主理想，且是局部主理想环，因此它有唯一的最大理想。

设R是一个有限链环，I是它唯一的最大理想，让γ是的I生成元，则

于是

由于R为有限环，所以在式(1)中的链不可能是无限的。因此，存在正整数i使设e是使= { 0}的最小正整数，这个数e叫做γ的幂零指数。使用R×表示R中所有在乘法运算下的单位作为的集合。记则F是一个域，称为主理想环I的剩余类域。设它的特征为素数p，则存在正整数q和r，使显然

下面给出2个引理[6]。

引理1[6]记号如上，对任意0≠r∈R，存在唯一整数i且0≤i≤e，使得r=μγi，这里μ是一个单位且在模γe-i下是唯一的。

引理2[6]设R是具有最大理想I=γ 的有限链环，γ的幂零指数为e。设 V⊆R 是R中元素在γ的模同余关系的等价类的代表元作成的集合。则：

1) ∀r∈R,存在唯一的r0,r1, … , re-1∈V ，使得

从引理2知道∀a∈R有唯一的表达式。

其中，ai∈F。

下面2个定义是由Dougherty和刘宏伟在文献[5]中给出的。

定义1[5]设i是一个任意正整数，令

其中，在 R 中，γi-1≠0，但γi=0。在R中，定义ii2种运算

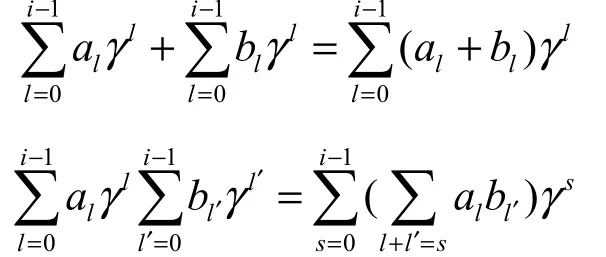
则 Ri是一个有限环。

注意到，当i=1时，R1=F；当i=e时，Re≅R。

易证明，对于任意i＜∞，环 Ri是有唯一最大理想γ的有限链环。

定义2[5]记号如上，设

则称R∞为形式幂级数环，显然且R∞为主理想数环。

定义3对于任意正整数i＜∞，定义映射

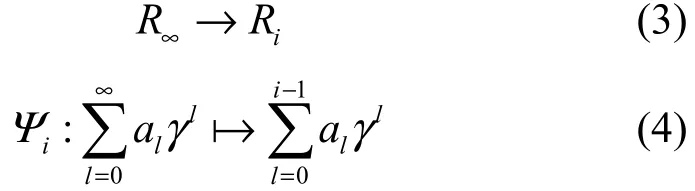
称Ψi为R∞到Ri的投射映射。

对于任意∀a,b∈R∞，易验证

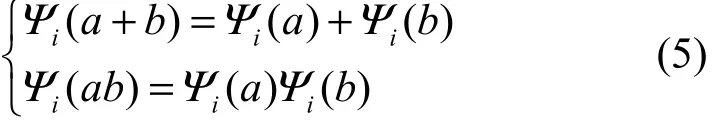
注意到，映射Ψi可以很自然地扩充成R∞n到 Rin的映射。

定义 4 如果C是R∞上码，对于任意i＜∞，称Ψi( C )是码C在环 Ri上的投影码。有时，用 Ci表示Ψi( C )。

由于循环码与多项式的剩余类环有密切关系。为此将等式（5）定义的映射引入到形式幂级数环R∞与有限链环 Ri的多项式中。

设

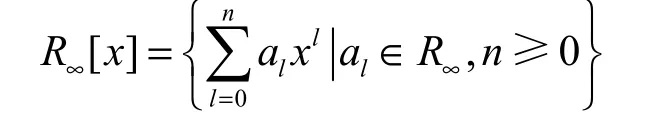
是环R∞上的多项式环。由于R∞为整环，因此 R∞[x]也为整环。

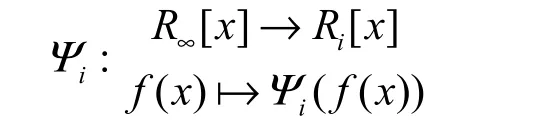
3 R∞上的循环码与负循环码

本节利用R∞上码C的投影码Ψi( C )的循环性来研究码C的循环性。

设λ是R∞上的任一单位，令对于若且则从而因此或

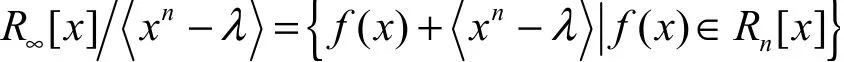
定义映射Pλ如下

特别地，如果取λ=1或λ=-1，得到下面2个映射P1和 P-1。

设C是 R∞n的任意集合，记

定义5 设C是R∞上长度n的线性码，如果对于任意有cn-2)∈C ，则称C为R∞上的λ循环码。 当λ=1时，称C为R∞上的循环码。当λ=-1时，称C为R∞上的负循环码。

引理3R∞上一个长度为n的线性码C是λ循环码，当且仅当 Pλ(C)是的理想。

证明设线性码C是R∞上λ循环码，则对于任意有cn-2)∈ C 。于是∈ Pλ(C)，由于

反之，当 Pλ(C)是的理想时，线性码C是R∞上一个长度为n的λ循环码，这是显然的事实。

推论1

1) R∞上一个长度为n的线性码C是循环码，

当且仅当 P1(C)是的理想；

2) R∞上一个长度为n的线性码C是负循环码，当且仅当 P-1(C)是的理想。

接下来，研究R∞上循环码与负循环码以及这类码的投影码。

设

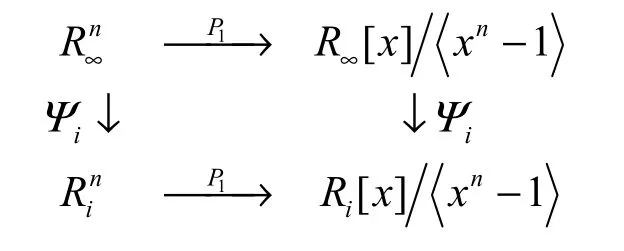
有了以上准备，就可以证明下面定理。

定理1记号如上。R∞上一个长度为n的线性码C是循环码，当且仅当对于所有i＜∞，Ψi( C )是Ri上的循环码。

证明先证明必要性。设C是R∞上的循环码，

则由推论1知 P1(C)是的理想。再由同态式(6)及上面的交换图，知道 Ψi(P1(C))是的理想。从而对于所有i＜∞，Ψi( C )是 Ri上的循环码。

同理可证如下定理及推论。

定理2记号如上，R∞上一个长度为n的线性码C是负循环码，当且仅当对于所有i＜∞，Ψi(C)是 Ri上的负循环码。

推论2设其中p为素数，则 ZP∞上的线性码为循环码当且仅当对所有i＜∞，Ψpi( C)为ZPi上的循环码。这里，ZP∞到 ZPi的映射Ψpi由定义。

4 中国积中的循环码

中国剩余定理在环上码的研究中有非常重要的应用[1,5,7]。在这一节，将用中国剩余定理研究中国积在什么条件下为循环码。

设R是一个环， I1,I2,… ,Is是R中两两互质的理想，且显然，映射

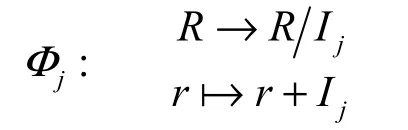
是一个自然同态，它可以自然扩充为下面映射：

易验证Φ是一个R模同构。记这个同构的逆为

如果 Rj= R Ij，则记对j = 1 ,2,… ,s ，设 Cj是 Rj上的码。让 C = C RT(C1,…,那么称C为码 C1,… ,Cs的中国积。

设 R1,… ,Rs是链环，其中Rj有唯一最大理想

e1esejγj和γj的幂零指数为ej，记

对于任意正整数i＜∞，由等式(4)定义的映射Ψi，可以得到下面映射（仍记为Ψi）：

于是，有下面交换图

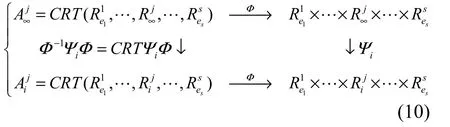
因此，环 Aij可以看成环 A∞j的投影。对1≤i＜ ∞ ，设Cij是 Rij上的码，而 C∞j是 R∞j上的码。记则由交换图(10)得到下面交换图

因此，对于所有i＜∞，在 Aij上的码 Cij可以看作 A∞j上码 C∞j的投影。

定理 3设分别是1的长为n的线性码是 A∞j上长为n循环码，对所有是 Aij长为n的循环码。

证明记号如上，有交换图

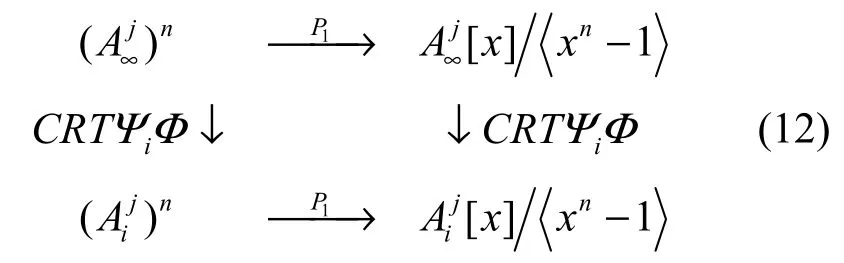
设 Cj是 Aj上的循环码，则 P(Cj)是∞∞1∞上的理想，故对于任意正整数i＜∞，结合同态式(5)及交换图(12)知道是的理想。再由交换图(11)知，是 Ai

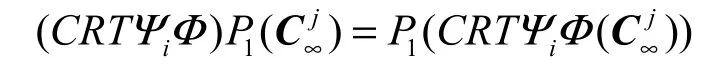
j的循环码。

[1] CALDEERBANK A R, SLOANE N J A. Modular and p-adic cyclic codes[J]. Designs,Codes,Cryptogr,1995,6∶21-35.

[2] NORTON G H, SALAGEAN A. On the structure of linear and cyclic codes over finite chain ring[J]. Appl Algebra Engrg Comm Comput,2000, 10∶489-506.

[3] KANWAR P, LOPEZ-PERMOUTH S R, Cyclic codes over the integers modulo pm[J]. Finite Fields Appl, 1997, 3∶334-352.

[4] DINH H, LOPEZ-PERMOUTH S R. Cyclic and negacyclic codes over finite chain rings[J]. IEEE Trans Inform Theory, 2004, 50∶ 1728-1744.

[5] DOUGHERTY S T, LIN H. Independence of vecter in codes over rings[J]. Designs,Codes, Cryptogr, 2009,51∶55-68.

[6] NORTON G H, SALAGEAN A. On the Hamming distance of linear codes over a finite chain ring[J]. IEEE Trans Inform Theory, 2000, 46∶1060-1067.

[7] DOUGHERTY S T, SKIROMOTO K. MDR codes over Zk[J]. IEEE Trans Inform Theory, 2000, 46∶265-269.