基于EM算法的改进OFDM时变信道估计

陈东华， 赵 睿

（华侨大学 信息科学与工程学院，福建 厦门 361021）

0 引言

为了抑制时变信道中 OFDM 系统子载波间干扰(ICI)，接收机必须获得精确的信道估计[1]，然而在时变信道环境中，传统的静态信道估计方案[2-3]不再适用。针对 OFDM 时变信道的估计，目前提出了很多方法[4-5]，但这些方法都具有很高的实现复杂度。文献[6]基于分段线性模型提出了一种低复杂度时变信道估计方法，该方法的优点是一个符号内只需估计时域平均信道脉冲响应(CIR)和信道变化斜率。基于分段线性模型的时变信道估计的性能依赖于符号时域平均CIR的估计精度，因此符号时域平均CIR的估计精度非常关键。为了提高符号时域平均CIR的估计精度，提出一种期望最大化(EM)辅助的信道估计与 ICI抑制的迭代算法，在 EM信道估计迭代过程中，通过ICI抵消来提高时域平均CIR的估计精度，从而提高时变信道估计的性能，该算法能在提高系统性能的同时保持较低的复杂度。

1 接收信号模型

解调后的接收频域信号可表示为[6]：

其中N为OFDM符号长度，H(k,k)为子载波X(k)上的信道频响(CFR)，Ic(k)为其它子载波对第k个子载波的ICI，W(k)是均值为零方差为2σ的频域加性高斯噪声。H(k,k)，Ic(k)的数学表达式分别为：

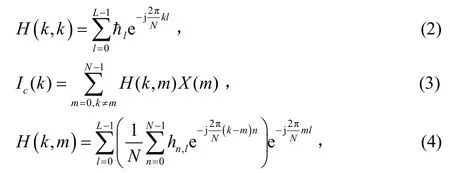
lCIR，hn,l为n时刻第l径的CIR。定义X=[X(0),…,X(N-1)]T，Y=[Y(0),…,Y(N-1)]T， ħl=[ħ0,…, ħL-1]T，则式(1)可表达为如下矢量形式：

其中W为加性高斯噪声矢量；Ic为ICI矢量；H为时变信道CFR矩阵，H的第(k,m)个元素为H(k,m)；FL表示N点DFT酉变换矩阵的前L列组成的子阵；diag(X)表示以矢量X为对角线元素的对角阵。

由式(5)可知，信道的时变带来ICI，为抵消ICI的影响，需要精确地估计出时变信道。同文献[6]，下面采用分段线性模型近似时变信道。记ħl,cur，ħl,pre分别为当前和前一个符号的第l径时域平均CIR，则当前符号前半时段信道线性变化的斜率为al=(ħl,pre-ħl,cur)/Ts，其中，Ts为符号持续时间，当前符号前半时段的时域CIR可表示为hn,l= ħl,cur+ ( N / 2 - n)Tsal( n = 0 ,1,… ,N 2) ，当前符号后半时段时域CIR hn,l(n=N/2+1,…,N-1)同理可求。一旦求得当前符号的时域CIR hn,l(n=0,1,…,N-1)，即可由式(2)，式(4)得到CFR并进行ICI抑制。

2 迭代信道估计

由前面的分析，时域平均CIR估计的精度是分段线性时变信道估计性能的关键，下面提出一种改进的分段线性时变信道估计方案。

假设发端在发送数据符号中等间隔插入梳状导频，则时域平均CIR可由导频估计得到[6]。仅利用导频通常不能得到可靠的信道估值，EM信道估计[7]是同时利用导频和数据的一种最大似然信道估计算法，通过迭代提高信道估计的精度。为提高信道估计的精度，下面采用EM算法来估计时域平均CIR。由式(5)，不考虑ICI的接收信号可表示为：

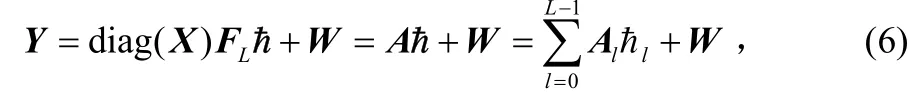
其中，A=diag(X)FL，Al表示矩阵A的第l列，Al的第k个元素记为A(k,l)。由式(6)可把式(1)写为：

定义“完整”数据矢量为Zk=[Z0(k),…,ZL-1(k)]T，其中Zl(k)=A(k,l)ħl+Wl(k)， Wl(k)是 W(k)的 任 意 分 解 ， 满 足∑lWl(k) = W(k)，利用Zl(k)，式(7)可表示为 Y (k)=∑lZl(k)。EM信道估计中，Y(k)被定义为“缺失”数据。由文献[7]，符号时域平均CIR的EM估计可表示为：

其中，i表示第i次迭代，βl满足∑lβl=1。同导频信道估计相比，EM算法提高了ħ的估计精度，但上述传统EM算法没有考虑ICI的影响，由式(1)可知，接收信号受ICI干扰，为降低ICI对时域平均CIR估计的影响，可在EM迭代过程中，根据时变信道分段线性近似嵌入ICI均衡和ICI抵消，在提高时域平均CIR估计的基础上提高分段线性时变信道估计的精度。嵌入ICI抵消后的EM信道估计步骤为：

①由估计出的符号时域平均CIR矢量ħ和对应的斜率计算CFR矩阵H，由H进行ICI均衡：σ2I )-1HHY ；

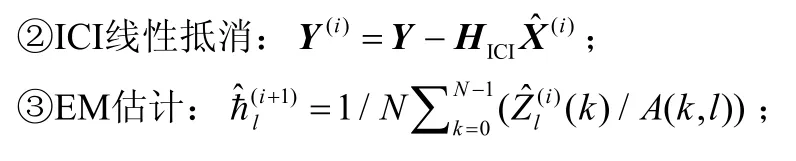
④若收敛或达到最大迭代次数则中止，否则返回步骤①。

其中步骤②中的 HICI为子载波间干扰矩阵，由对 CFR矩阵H的对角线元素置零得到。由步骤①可知，ICI均衡算法需要N×N的矩阵求逆，复杂度很高。研究表明[8]，ICI随子载波间隔的增大而迅速递减，某一子载波上的ICI主要来自相邻的若干个(如 D个)子载波，以此为基础，文献[8]提出了一种带状均衡器来降低 ICI均衡的复杂度。为了降低ICI均衡和抵消的复杂度，这里采用文献[8]的方法对 H做带状近似。由文献[7-8]，带状均衡器和 EM 算法的复杂度分别为 O(D2N)、O(N)，通常 D＜＜N，因此，整个算法的复杂度与N近似成线性关系。

3 仿真分析

仿真参数：OFDM系统采用QPSK调制，每符号子载波数为N=64，等间隔插入4个导频子载波，多径信道路径数L=2，每径的功率随时延服从指数衰减分布，且不同路径间相互独立。

图1和图2比较了基于导频的分段线性时变信道估计与EM辅助的分段线性时变信道估计的误比特率性能，两者均采用带状ICI均衡，且考虑的子载波间隔为D，图1和图2分别对应时变信道归一化多普勒频率fdTs为0.05和0.075时的情况，其中，fd为多普勒频率[9]。作为参考，同时给出了导频信道估计下单抽头均衡器的误比特率性能。由图可见，由于考虑了ICI的影响并采取了抑制措施，基于导频的分段线性时变信道估计并结合带状均衡比单抽头均衡具有更好的系统性能，而采用EM辅助的带状ICI抑制与仅采用导频的带状ICI抑制相比，系统性能得到进一步较大提高，这是由于导频个数很少，仅采用导频的时变信道估计不能得到可靠的信道估值，而EM迭代算法提高了符号时域平均CIR的估计精度，从而也提高了分段线性时变信道的估计性能。同时可以看到，考虑的子载波间隔D为4时，系统性能便有显著提高，而继续增大D，系统性能提高有限，这是由于ICI随子载波间隔的增加而逐渐递减，距离较远的ICI能量很小，忽略它们所带来的性能损失非常有限。

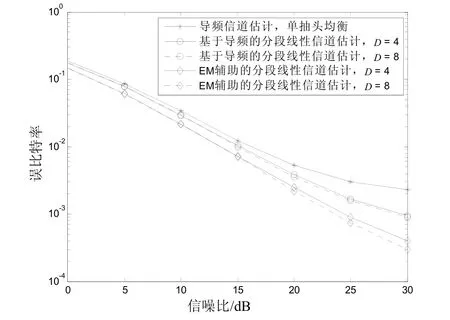
图1 误码率性能比较(fdTs=0.05)

图2 误码率性能比较 (fdTs=0.075)

通过仿真和分析可知，提出的改进算法不仅能很好地改善系统性能，而且迭代算法中采用了带状 ICI均衡和抵消，具有较低的计算复杂度。

4 结语

研究了基于分段线性模型的OFDM时变信道估计问题，提出了利用EM迭代和ICI抑制来提高时变信道估计性能的改进算法，仿真和分析表明，提出的改进算法能有效改善时变信道OFDM系统的误比特率性能；同时，提出的改进算法复杂度低，便于系统实时实现。

[1] 洪利, 马俊飞, 张亮, 等.移动WIMAX下OFDM载波间干扰消除[J].通信技术, 2007, 40(12)： 68-71.

[2] 郝国虎, 尹志伟, 万毅. 一种新的OFDM联合信道估计方法[J]. 通信技术, 2010, 43(1)： 40-42.

[3] 李勇, 李雀. OFDM系统中多导频的FFT信道估计算法[J]. 信息安全与通信保密, 2008(03)：30-33.

[4] CHOI Y S, VOLTZ P J, CASSARA F A. On Channel Estimation and Detection for Multicarrier Signals in Fast and Selective Rayleigh Fading Channels[J]. IEEE Transactions on Communications, 2001, 49(08)： 1375-1387.

[5] HIJAZI H, ROS L. Polynomial Estimation of Time-varying Multi-path Gains with Intercarrier Interference Mitigation in OFDM Systems[J]. IEEE Transactions on Vehicular Technology, 2009, 58(01)： 140-151.

[6] MOSTOFI Y, COX D C. ICI Mitigation for Pilot-aided OFDM Mobile Systems[J]. IEEE Transactions on Wireless Communications, 2005, 4(02)： 765-774.

[7] MA X, KOBAYASHI H, SCHWARTZ S C. EM-based Channel Estimation Algorithms for OFDM[J]. Eurasip Journal on Applied Signal Processing, 2004(10)： 1460-1477.

[8] RUGINI L, BANELLI P, LEUS G. Simple Equalization of Timevarying Channels for OFDM[J]. IEEE Communications Letters,2005, 9(07)： 619-621.

[9] 唐云, 王玲. MIMO-OFDM 系统信道估计算法研究[J], 信息安全与通信保密, 2007(05)：81-83.