一种自适应通道均衡技术及其实现

刘 毅 ， 何 春 ， 张旭东

（电子科技大学 a.电子科学技术研究院；b.通信与信息工程学院，四川 成都 611731）

0 引言

N元自适应天线阵包含N路信号接收通道，每个接收通道都包括低噪放、混频、中放、滤波器等模拟器件。接收通道中的各个部件在制造工艺上存在的各种误差、器件老化、下变频的正交误差等都会引起通道幅相特性的变化[1]，这种变化称为通道失配。自适应天线通道间的失配会导致抑制干扰的零陷深度变浅、方向图副瓣电平升高，严重影响了自适应阵列天线的性能[2]。对于窄带天线系统，可将通道失配视为载频的增益和相位的失真，对于宽带天线系统应该在整个频带内考虑其幅度和相位的不一致性。传统的单频点信号校正法只能对接收频带内的某一频点失配进行补偿，而不能对整个频带进行通道失配补偿，因此它不能用于校正宽带天线系统的通道失配。鉴于此，提出了一种基于VSS算法的自适应均衡方法，该方法能够在很宽的频带范围内对幅度和相位进行补偿，适用于宽带天线系统的通道均衡。

1 通道均衡原理

假设自适应天线系统由N个阵元组成，与阵元相连的N个接收通道的传输函数为 c1(ω),c2(ω),…,cN(ω)。选取畸变最小的接收通道作为参考通道，设其传输函数为Href(ω)，其余各通道后串接一个均衡器来实现阵元通道的幅度和相位调整，对于N元阵列天线需要N-1个均衡器，设均衡器的传输函数为 Ei(ω)，经过均衡后的通道传输函数为 Hi(ω)，则：

其中 N为天线阵元数。如果能使均衡后的通道传输函数Hi(ω)等于参考通道的传输函数 Href(ω)，即：

那么就实现了通道均衡，故均衡滤波器的传输函数应该设计为： Ei( ω) = Href( ω) ci(ω)。

2 自适应算法

根据自适应滤波算法优化准则的不同，自适应滤波算法可以分为LMS算法和最小二乘（RLS）算法[3]。RLS算法对输入信号的自相关矩阵的逆进行递推估计更新，收敛速度快。但是一旦自相关矩阵的逆失去了正定性，就会引起算法的发散，而且RLS算法的计算复杂度很高，所需的存储量很大，不适合在FPGA中实现。LMS算法不需要计算自相关矩阵，计算复杂度低，便于工程实现，但这种算法受梯度噪声影响大，在处理强相关信号时性能下降很快，而且难以兼顾收敛速度和收敛精度。鉴于 LMS算法的缺点很多学者提出了各种各样的变步长LMS算法[4-7]，变步长LMS算法在自适应的初始阶段误差较大，对应的步长也较大，算法收敛速度快，随着算法逐渐进入稳定误差减小，步长也相应的减小，因此在最佳权系数附近产生较小的失调。变步长 LMS算法中的VSS算法在最佳权值附近产生的失调比较小，且其步长因子计算公式只涉及到乘法和加法，易于FPGA实现，不像SVS算法[5]那样需要幂运算。鉴于以上分析选择VSS算法作为自适应均衡器的滤波算法。

LMS算法是基于最小均方误差和最陡梯度下降法提出的，根据这个准则来对滤波器的系数进行更新，设输入向量为X(n)，权向量为ω(n)，参考信号为d(n)，步长为µ，则标准 LMS算法可以描述为如下[8]：首先初始化滤波器系数ω( 0 ) = 0 ，对于n=0,1,2…计算：

其中 e(n)为误差，步长因子µ用来控制算法的稳定性和收敛速度，LMS算法的收敛条件为 0 ＜ u ＜ 1/λmax,λmax为输入信号自相关矩阵的最大值。由标准 LMS算法的描述可以看出其步长是固定的，而 VSS算法的步长是由误差自适应控制的，其计算公式为[7]：

其中()en为误差信号，由公式(5)给出，maxµ一般选择标准LMS算法的不稳定步长点，minµ用于控制算法的最小步长，可以根据具体情况而定，a为遗忘因子，一般非常接近1以获得最大可能的收敛速度。参数γ一般取值比较小，用来控制算法的失调和收敛时间。把公式(6)带入到公式(5)中就得到了VSS算法的权值计算公式。

3 通道均衡的实现

接收通道校正有远场校正和内部校正两种方式，远场校正是将测试信号从远场发射，测试信号经接收机天线阵元通道进入自适应均衡器，在均衡器中实现接收通道的幅相特性校正；内部校正是直接把测试信号输入至接收机天线阵元通道做一致性校正，为了保证用于通道均衡的N路信号的一致性，将测试信号输入到具有N个输出端口的功分器，把功分器的输出信号注入各阵元通道。图1示出了内部校正的自适应均衡的原理图。自适应天线阵元通道特性的改变是缓慢的，在一次通信过程中可以认为天线阵元通道的特性不改变。因此可以在每次通信前对阵列天线阵元通道进行校正，校正完成之后再开始正常的通信，即从时间上把校正和正常通信分开。在阵元通道校正过程中，自适应滤波器使各阵元通道特性趋同时，自适应滤波器的系数几乎不再改变，将这些系数固定下来用于均衡信道，然后停止注入校正信号，此时正常的通信就可以开始了。

图1 自适应均衡原理

图2 自适应均衡器结构

自适应均衡器在 FPGA中实现，FPGA中的程序采用Verilog HDL编写，开发环境为QuartusⅡ7.2，整个系统采用61.38 MHz的系统时钟。把自适应滤波器的阶数设为12，各通道AD芯片的输出位数为8 bit。众所周知，浮点运算具有较高的运算精度，但其消耗的硬件资源多，而且速度比定点运算慢，为了节约硬件资源和提升运算速度，FPGA内部的数据运算全部采用定点运算。为了确保运算精度，FPGA内部采用16位的硬件乘法器来实现乘法。用Verilog HDL编写完整个工程后用QuartusⅡ7.2综合得到的自适应均衡器顶层模块 RTL视图，RTL视图即为寄存器传输级视图，它是在对源代码编译后再现设计的寄存器传输级原理图。图2是根据RTL视图绘出的自适应均衡器结构图。

为了简明起见，以下仅分析两个阵元通道的情况，对于两个以上阵元的情况，无非就是多了几个待调整通道，所有待调整通道的输出信号和两个阵元情况下的待调整通道输出信号作同样处理即可。参考通道的输出信号作为均衡器的参考信号 d (n)，待调整通道的输出信号作为均衡器的输入信号x(n)，因为AD芯片输出的数据为8 bit，而FPGA内部的乘法器都是 16位的，所以在 d (n)和 x(n)用于运算之前，必须将它们扩展成16 bit。把扩位后的 x(n)送入到12阶的移位寄存器产生所需的输入信号矢量[x(n),x(n -1),…, x (n - 1 1)]T；把寄存器中的12维列向量送入到加权模块中与权值系数相乘产生 y (n)；把 y (n)送入到误差计算模块和 d (n)作差产生误差信号 e(n)，特别需要注意的是 d (n)和 y (n)必须在时序上对齐才能产生正确的误差信号 e(n)。滤波器是12阶的，需要经过12次复乘运算和11次复加运算才能得到 y (n)，而 d (n)直接由输入端输入，所以 d (n)必须经过适当的延迟才能和 y (n)在时序上对齐，因此在 d (n)的输入端和误差计算模块之间需要插入一个延时模块以保证 d (n)和 y (n)必须在时序上对齐。由于该均衡器使用的是VSS算法，和传统LMS算法实现均衡器相比，需要增加一个收敛因子计算模块来计算权值，把误差信号送入到步长计算模块中按照公式(7)和公式(8)更新步长因子，把更新后的步长因子、误差信号和输入信号矢量送入到权值计算模块中用于更新权值。

4 仿真分析

仿真时输入到自适应天线的信号是带宽为 10.23 M 的QPSK信号，用MATLAB软件模拟输入信号和通道特性，产生参考通道输出信号 d (n)和待调整通道的输出信号 x (n)。用Modelsim对综合后的电路进行仿真分析，通过仿真得出通道均衡前后的幅度特性和相位特性，图3所示的是均衡前后待调整通道和参考通道的幅度失配，图中横轴显示的是偏移中心频率的值；图4所示的是均衡前后待调整通道和参考通道的相位失配，均衡前相位差最大值达到58度，而校正后相位差最大只有0.22度。由仿真结果可以看出，在20 M的频率范围内阵元通道的幅度失配和相位失配都得到了很好的校正。

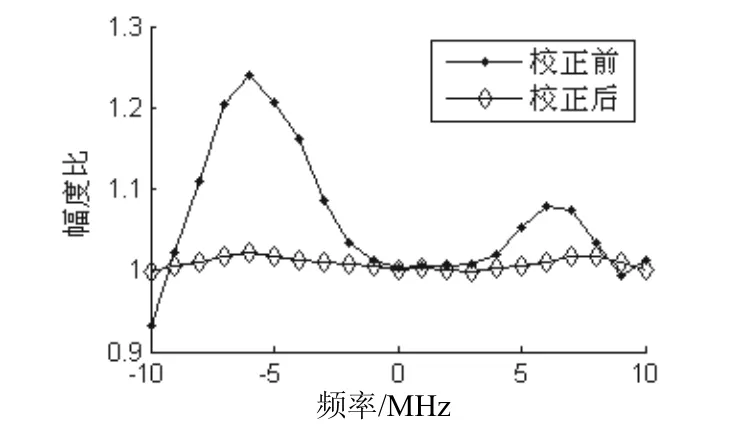
图3 校正前后的幅度失配

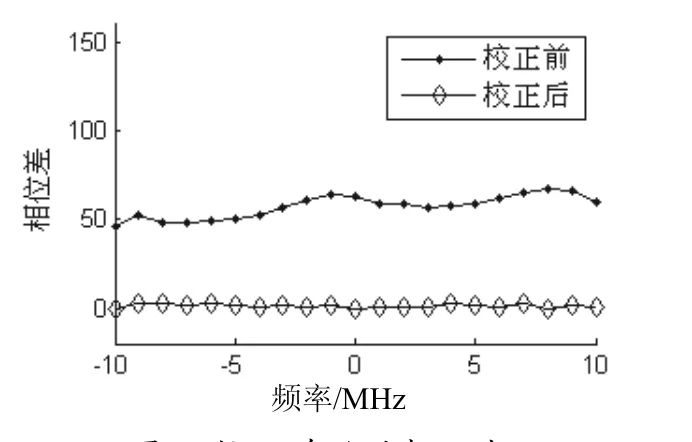
图4 校正前后的相位失配

5 结语

为了解决宽带天线幅度相位不一致的问题，提出了一种自适应通道均衡方法对宽带阵列天线的通道失配进行校正，并给了其FPGA实现方案。从算法的复杂度和目前FPGA器件的运算能力两方面考虑选择了VSS算法，VSS算法有其局限性但易于实现。随着集成电路的发展必将诞生运算能力更强的FPGA，这样就可以选择运算复杂度更高的算法来提升通道均衡精度；另外为了节省硬件资源和确保运算速度，采用了定点运算，众所周知定点运算的精度远不如浮点运算，在硬件资源丰富和运算速度要求不高的情况可以把 FPGA内部运算改为浮点，这样可以进一步提高通道均衡的精度。

[1] 王青松,习友宝,肖鹏,等.一种数字矢量调制幅相误差的校正方法[J].通信技术，2010,43(05)：19-23.

[2] 曾奋，董英凝，邓维波.均匀线阵幅相误差和互耦效应的自校正[J].通信技术，2010,43(04)：31-33.

[3] 龚耀寰.自适应滤波-时域自适应滤波和智能天线[M]. 第二版.北京：电子工业出版社,2003：36-99.

[4] 邓江波，侯新国，吴正国.基于箕舌线的变步长LMS自适应算法[J].数据采集与处理,2004,19(03)：282-285.

[5] 覃景繁，欧阳景正.一种新的变步长LMS自适应滤波算法[J].数据采集与处理,1997，12(03)：44-47.

[6] ABOULNASR T, MAYYAS K. A Robust Variable Step-size LMS Type Algorithm： Analysis and Simulations [J]. IEEE Trans on Signal Processing, 1997,45(03)：631-639.

[7] KWONG R H, JONSTON E W. A Variable Step Size LMS Algorithm[J].IEEE Trans on Signal Processing,1992,40(07)：1633-1642.

[8] Widrow B, Hoff M E Jr. Adaptive switching circuits[J]. IRE WESCON Conv. Rec., 1960(04)：96-104.