有机玻璃裂纹扩展双参量驱动力模型

宋全超， 张建国， 乙晓伟， 王 泓

(西北工业大学材料学院，西安 710072)

通常用应力场强度因子范围ΔK作为裂纹扩展的驱动力，并得相应的da/dN-ΔK曲线，来估算构件疲劳裂纹扩展寿命，但是不同应力比所对应的da/dN-ΔK曲线不同，所以寻找一个包含应力比对裂纹扩展速率曲线影响的裂纹扩展驱动力ΔKdrive，使不同应力比所对应的da/dN-ΔKdrive曲线重合在一起，有利于为研究不同应力比条件下的裂纹扩展速率曲线节省很多时间和成本。

自从Elber［1］试验发现裂纹闭合效应现象以来，裂纹闭合现象作为影响疲劳裂纹扩展行为的主要机制已被广泛接受，认为裂纹扩展的驱动力是有效应力场强度因子ΔKeff，其表达为:

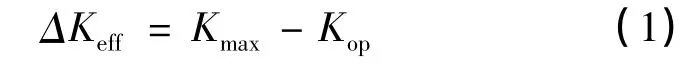
式中，Kop是裂纹张开时应力对应的场强度因子，Kmax是最大应力场强度因子，但是Kop因测量技术和测量位置的不同，是个变化的值［2，3］。而Sadanada和Vasudevan［4，5］认为裂纹闭合效应对裂纹扩展的阻碍作用被夸大了，并且Sadanada［6］提出裂纹扩展的动力是Kmax和ΔK，两者在不同的阶段起主导作用，裂纹尖端单调塑性变形区的大小主要受到Kmax控制，循环塑性区的大小受到ΔK参数控制。为了避免考虑裂纹闭合效应，结合Sadanada提出裂纹扩展的动力参数 Kmax和 ΔK，Daniel Kujawski［7］提出了新的包含应力比对裂纹扩展速率影响的新参数K*，其表达式为:

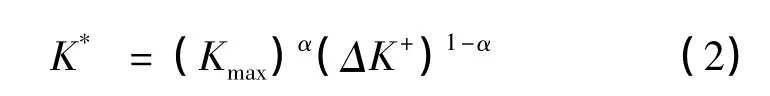
式中ΔK+为正应力对应的应力场强度因子范围，当R ＞0时，ΔK+=ΔK;当 R≤0时，ΔK+=Kmax。此裂纹扩展驱动力模型在大多数金属材料中得到验证，对于大多数金属材料，Kujawski给出相关参数α≅0.5。

其中参数K*中相关参数α的计算方法为式(2)两边同时取对数，得到:

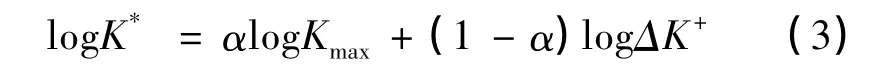
式(3)经过变形得到:

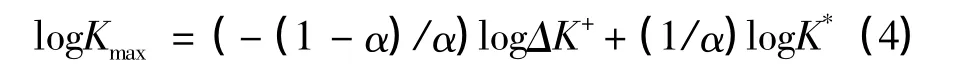
从式(4)可以看出，对于一定的裂纹扩展速率，不同的应力比将对应不同的(ΔK+，Kmax)，在双对数坐标中，直线的斜率为－(1－α)/α，由此就可以计算得到一定裂纹扩展速率所对应的参数K*中的αi，计算不同的裂纹扩展速率所对应的αi，并计算其均值αa，就是参数K*中的相关参数α值。

目前，有机玻璃作为飞机构件，遇到的重要问题之一就是有机玻璃的损伤容限和有机玻璃构件的疲劳寿命评估［8］。对有机玻璃构件的疲劳裂纹扩展寿命评估，主要是依靠试验，用ΔK作为裂纹扩展的驱动力，从而得到不同应力比条件下的 da/dN-ΔK曲线，如贾敬华［9］对不同应力比条件下中部区裂纹扩展速率的描述。而采用双参量裂纹扩展驱动力模型研究包含应力比对裂纹扩展速率影响的文献还比较少，本工作主要研究有机玻璃Ⅱ和Ⅲ区的裂纹扩展速率，用双参量裂纹扩展驱动力模型解释应力比对裂纹在有机玻璃内扩展速率的影响，将不同应力比的裂纹扩展曲线归一化到一条曲线上。

1 疲劳裂纹扩展速率试验

在本项研究工作中，疲劳裂纹扩展试验试件采用中心穿透的裂纹孔MT试样［10］，其尺寸为320mm(长)×100mm(宽) ×16mm(厚)。应力场强度因子幅值计算公式为:

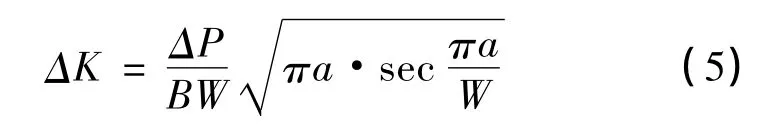
式中，ΔP为循环载荷范围，ΔP=Pmax－Pmin(R≥0)，ΔP=Pmax(R＜0)。B为试样厚度，W为宽度，a为计算裂纹长度。

疲劳裂纹扩展试验在岛津EHF-EA10电液伺服疲劳机上进行。室温，加载波形为正弦波，频率2.5Hz，应力比 R= －0.4，0.1 和 0.4。用移动式显微镜测量裂纹扩展增量，精度为0.01mm。

2 结果与分析

2.1 试验结果

试验结果及 Forman公式［11］拟合曲线见图1。从图1可见，三个应力比的裂纹扩展速率曲线都包含中部区和加速扩展区，用Forman公式拟合的结果见表1，Forman公式为:

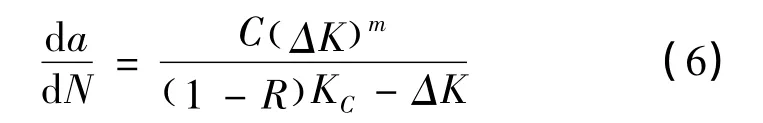
式中，KC是断裂韧度，ΔK是应力场强度因子范围，C和m是拟合参数。

从Forman公式拟合的参数得出，相同的ΔK，应力比越大，裂纹扩展速率就越大，裂纹扩展速率曲线的上限值(1－R)KC则越小，使得裂纹扩展较早进入加速扩展区;中部区直线的斜率m与截距C随着应力比的增大而增大。从图1拟合曲线与观察点的吻合性和表1中拟合结果的相关系数可知，Forman公式能够很好地表征有机玻璃裂纹扩展加速扩展区和Pairs区。

表1 疲劳裂纹扩展速率曲线Forman公式拟合结果Table 1 Constants in the Forman's law derived from the experimental results

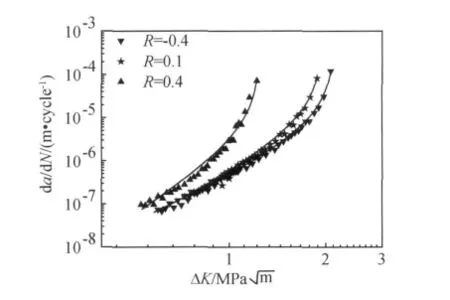
图1 用ΔK定义的裂纹扩展速率Fig.1 Fatigue crack growth data of orientation PMMA as a function of ΔK and the fitted equations by Forman's law

2.2 双参量裂纹扩展驱动力模型

依据Kujawski提出的双参量裂纹扩展驱动力模型中的K*，不同应力比所对应的曲线将会重合在一起。对于不同应力比，用Forman公式拟合所得参数应该是一个恒定量。

式(2)中α值反映Kmax与ΔK+作为裂纹扩展驱动力主次关系，当α值较大时，K*参数对Kmax的敏感性越大，即Kmax在裂纹的扩展动力中起主导作用，ΔK+起次要作用;相反，α值较小时，ΔK+在裂纹的扩展动力中起主导作用。

根据α值的计算方法，计算参数K*所对应的α值，发现对于有机玻璃，α值随裂纹扩展速率的增大而增大:当 da/dN=9×10－7m/cycle时，α1=0.2;当 da/dN=5×10－5m/cycle时，α2=0.5;当 da/dN→∞(ΔK→(1－R)KC)时，αb=1.1。所以对于有机玻璃而言，随着裂纹扩展速率的增大，裂纹扩展驱动力的主次由ΔK+逐渐过渡到Kmax，并且加速区与中部区参数K*中α值差别较大，因此，将α的均值αa代入参数K*时，对于中部区，夸大了Kmax的作用以及应力比对中部区的影响;对于快速扩展区，反而夸大ΔK+的作用，此时用α均值作为K*中的α值是不合理的。

简单认为 αa为 α1，α2和 αb三者的均值，αa=0.6。将 αa=0.6 和 αb=1.1 分别代入参数 K*，得到不同应力比所对应的裂纹扩展速率曲线和如图2和图3所示。从图2和图3可以看出，参数K*中的α值越大，应力比 R=0.4和R=0.1对应的裂纹扩展速率曲线右移，无论是αa=0.6或者αb=1.1，都不能将不同应力的裂纹扩展速率曲线归一化处理。当αa=0.6时，仅归一化应力比R=0.4，R= －0.4 和 R=0.1 曲线中部区的小部分。当 αb=1.1 时，参数 K*=(Kmax)α(ΔK+)1－α能够很好地归一化应力比 R=0.4，R=－0.4和 R=0.1加速快展区的尾部以及R= －0.4和 R=0.1 的中部;对于中部区，相同的裂纹扩展动力参数K*，应力比R=0.4的裂纹扩展速率反而比R=－0.4和R=0.1对应的裂纹扩展速率低，与实际不符。这主要因为ΔK相同时，R=0.4所对应的Kmax较大，αb=1.1时，虽然能够解释应力比对加速区的影响，但夸大了Kmax在中部区的作用，导致高估应力比R=0.4的裂纹扩展寿命。

为了使相关参数α反映不同裂纹扩展速率区域裂纹扩展驱动力的主次变化，需要提出一个裂纹扩展速率的函数α=f(da/dN)或者应力场强度因子的函数α=f(ΔK)来表征不同裂纹扩展区域动力ΔK+和Kmax对参数K*的贡献。

裂纹扩展速率由中部区到近门槛值区转变时，也伴随着裂纹扩展驱动力由ΔK+到Kmax的主次转变，Sudip Dinda［12］用一个函数 α(ΔK)=α0g(ΔK)取代α具体值，其中α0是ΔK→ΔKth对应的裂纹扩展速率计算得到的α值，α(ΔK)随着裂纹扩展速率的降低而增大，从而使得K*参数能够很好解释应力比对近门槛值区和中部区的裂纹扩展速率的影响，其中函数g(ΔK)=exp(1－ΔK/ΔKth)。

对于裂纹的扩展速率曲线由加速区到中部区，提出了一个新相关参数 αM=αbf(ΔK)，其中，f(ΔK)=exp(1－(1－R)KC/ΔK)，αb是 ΔK→(1－R)KC时，对应的裂纹扩展速率计算得到的相关参数 α 值。当 ΔK→(1－R)ΔKC时，f→1，能够反映加速区裂纹扩展驱动力主要是Kmax。而随着ΔK的降低，裂纹的扩展由加速区转到了中部区，f→0，αM=αbf(ΔK)的值逐渐减小，1－αM值相应的增大，反映了裂纹扩展驱动力由Kmax→ΔK+的逐步过渡。从而得到一个适合于中部区和加速区，修正的裂纹扩展双参量动力根据修正的两参量驱动力K*M，本工作得到不同应力比所对应的裂纹扩展速率曲线，如图4所示。

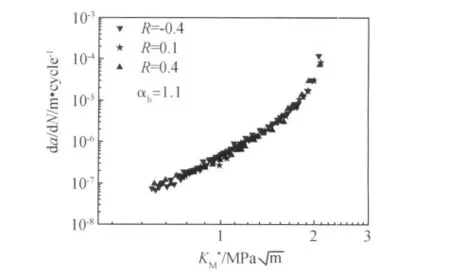
图4 用K定义的裂纹扩展速率Fig.4 Fatigue crack growth data of orientation PMMA as a function of K

从图4可以看出，对于定向有机玻璃YB-DM-11，K*M参数能够很好地解释应力比对裂纹扩展速率的影响规律。由此就得到包含应力比对裂纹扩展速率影响的Forman公式表达式:

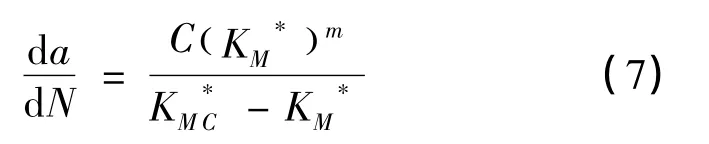
式中，KM*C是试件断裂瞬间K*M对应的最大值，即和m是拟合参数。

对于参数 K*M，当 R≤0时，ΔK+=Kmax，此时，，最终不同应力比R=0.4和R=0.1的裂纹扩展速率曲线与曲线重合。

3 结论

(1)Forman公式能够很好拟合YB-DM-11有机玻璃中部区和快速扩展区，应力比越大，拟合参数C和m越大，(1－R)KC的值变小，导致裂纹扩展较早进入加速扩展区。

(2)将双参量裂纹扩展驱动力模型中的α值用函数αM=α1f(ΔK)代替，得到修正的双参量裂纹扩展驱动力K*M，能够反映裂纹扩展由中部区过渡到加速区ΔK+和Kmax的转变，使双参量裂纹扩展驱动力模型很好地解释应力比对有机玻璃裂纹扩展中部区和加速区的影响。

(3)对于参数K*M定义应力比R=－0.4，R=0.1和 R=0.4的裂纹扩展速率曲线，与应力比R=－0.4时，Kmax定义的裂纹扩展速率曲线重合。

［1］ELBER W.The significance of fatigue crack closure［C］//POSEN Feld M S.Damage tolerance in aircraft structure.ASTM STP 486.Philadelphia(PA):American Society for Testing and Materials，1971:230 －242.

［2］MACHA D E，CORBLY D M，JONES J W.On the variation of fatigue crack opening loading with measurement location［J］.Experimental Mechanics，1979，19:207 －213.

［3］SHIN C S，SMITH R A.Fatigue crack growth from sharp notches［J］.International Journal of Fatigue，1985，7:87 －93.

［4］SAGANANDA K，VASUDEVAN A K.Analysis of fatigue crack closure and threshold［C］//ERDOGAN F.Fracture Mechanics:Vol 25.Philadelphia:American Society for Testing and Materials，1995:484 －501.

［5］SADANANDA K，VASUDEVAN A K.Short crack growth behavior［C］//PIASCIK R，DOWLING N，NEWMAN J.Fatigue and Fracture Mechanics:Vol 27.Philadelphia(PA):American Society for Testing and Material，1997:301 －316.

［6］SADANANDA K，VASUDEVAN A K.Crack tip driving forces and crack growth representation under fatigue［J］.International Journal of Fatigue，2004，26:39－47.

［7］KUJAWSKI D.A fatigue crack driving force parameter with load ratio effects［J］.International Journal of Fatigue，2001，23(supl):239－246.

［8］姚卫星.飞机结构疲劳寿命分析的一些特殊问题［J］.南京航空航天大学学报，2008，40(4):433－441.

［9］贾敬华，李亚智，肖健.YB-MD-3有机玻璃的疲劳裂纹扩展性能研究［J］.航空材料学报，2006，26(5):109－112.

［10］GB/T 6398.金属材料疲劳裂纹扩展速率试验方法［S］.2000.

［11］FORMAN R G，KEARNEY V E，ENGLE R W.Numerical analysis of crack propagation in cyclic-loaded structures［J］.Journal Basic Engineering，1967，89:459 －464.

［12］DINDA S，KUJAWSKI D.Correlation and prediction of fatigue crack growth for different R-ratios using Kmaxand ΔK+parameters［J］.Engineering Fracture Mechanics，2004，71:1779－1790.