一个求解非线性互补问题的光滑化全局收敛性算法
2011-09-09何婵
何婵
(武夷学院数学与计算机系,福建武夷山3543 00)
一个求解非线性互补问题的光滑化全局收敛性算法
何婵
(武夷学院数学与计算机系,福建武夷山3543 00)
求解非线性互补问题的一种方法是将其转化为非光滑方程组。本文通过引进一个基于F isc h e r-B u rm e iste r函数的光滑N C P函数[8],建立了求解P0函数非线性互补问题的一个新的光滑牛顿算法。这个算法在每步迭代中只需要解一个光滑方程且不要求给出具体光滑因子下降的过程。在一定的条件下,证明了该算法的全局收敛性。数值试验表明该算法是有效的.
非线性互补问题;光滑牛顿算法;全局收敛性.
§1引言
考虑如下的P0函数非线性互补问题(简记为N C P(F)):求一个向量x∈Rn,使得
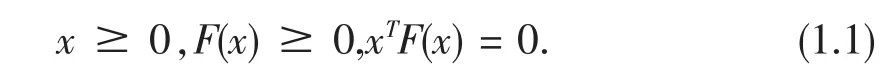
这里F(x):Rn→Rn是一个连续可微P0函数(见文[1])。
非线性互补问题是数学规划的一个基本问题,在工程和经济等领域都有非常重要的应用,感兴趣的读者可以参考文献[2,3]。
目前,求解非线性互补问题的一类重要方法是利用所谓的互补函数将N C P(F)转换成非线性方程组或非线性最优化问题来求解。本文将通过引进一个光滑N C P函数来建立求解N C P(F)的光滑牛顿法。并证明了所提出的算法是适定的。同时证明了在一定的条件下该算法是全局收敛的。
本文的结构如下:§2主要介绍一个光滑函数及其性质;§3介绍算法并证明算法是适定的;§4讨论算法的总体收敛性;§5为小结。
§2光滑函数及其性质
首先,给出F isc h e r-B u rm e iste r函数[4]:
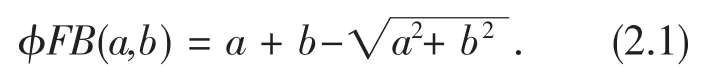
F isc h e r-B u rm e iste r函数有很多好的性质,在求解N C P(1.1)时,一般都以F isc h e r-B u rm e iste r函数(2.1)作为N C P函数(参见[5,6,7]),但它有一个明显的不足,即F isc h e r-B u rm e iste r函数在(a,b)=(0,0)点是不可微的,因此给算法的收敛性分析带来了困难,于是各种光滑化方法应运而生。
本文讨论了一个光滑N C P-函数[8]如下
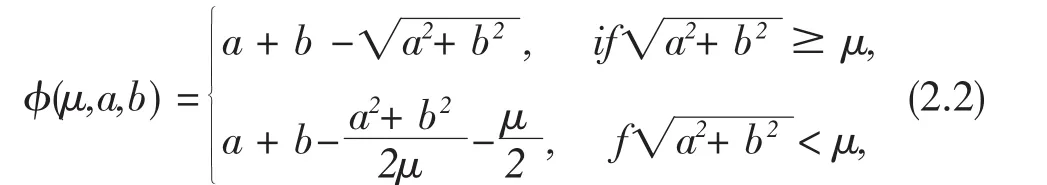
其中μ>0为光滑参数。这个光滑的N C P-函数有很好的性质,下面列出了其中的两个基本性质。
性质2.1(1)对任意的(μ,a,b)∈R++×R2,我们
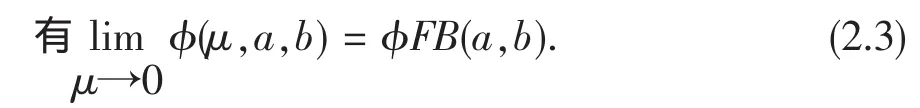
(2)对任意的μ1,μ2∈R++,我们有
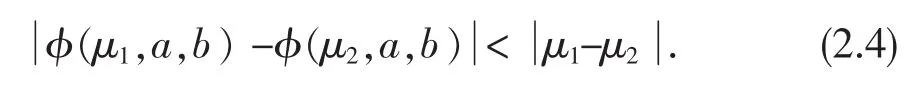
通过简单的计算,可得
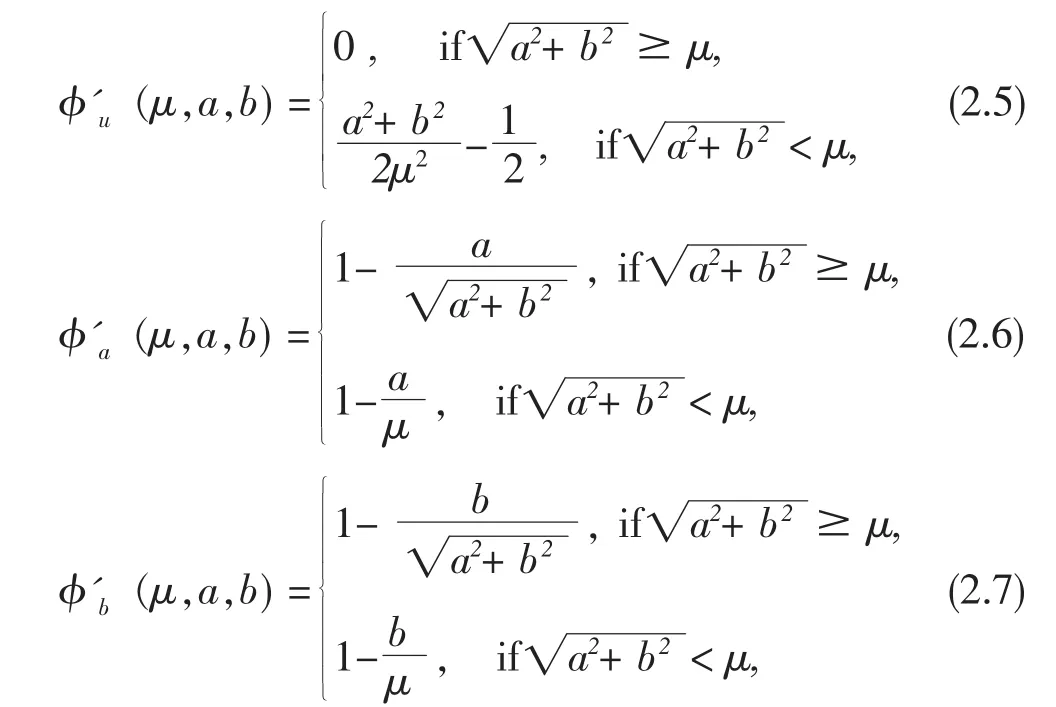
显然对于任意的μ>0,准'μ,准'a,准'b都是连续的,且有
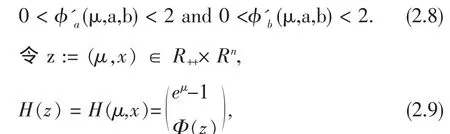
其中
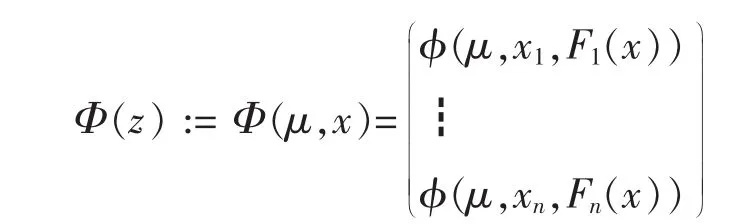
不难证明,求解(1.1)等价于求解下面的非线性方程组

引理2.1设H:R++×Rn→Rn+1由(2.9)定义。那么H在R++×Rn连续可微,且其Ja c o b i矩阵为
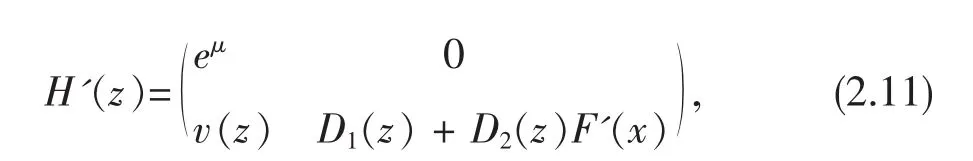
其中
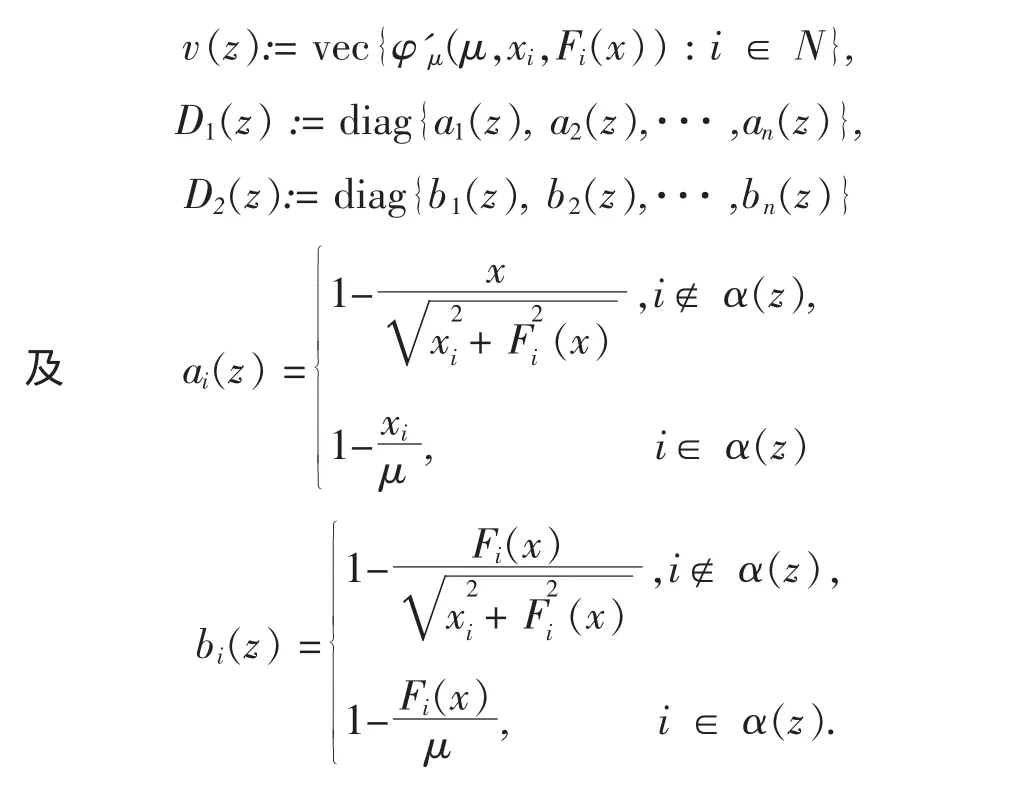
这里,指标集
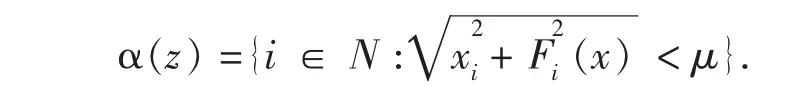
若F是P0-函数,则H'在R++×Rn非奇异。
证明:矩阵(2.11)可通过具体计算得到。由(2.8)不难发现
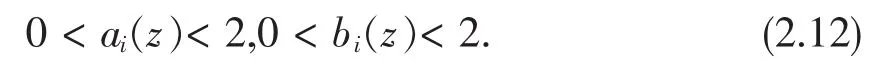
(2.11)可通过计算可以得到。由于eμ>0,因此,只需证明D1(z)+D2(z)F'(x)是对称正定的。事实上,注意到对角矩阵D1(z)和D2(z)的对角元素都恒为正数,而Ja c o b i矩阵F'(x)是P0-矩阵(因F是P0-函数),根据P0-矩阵的性质可以推得对称矩阵D2(z)F'(x)的所有主子式是非负的,从而D1(z)+D2(z)F'(x)是对称正定的,因而是非奇异的。由此可得,H'(z)也是非奇异的。证毕。
§3光滑化牛顿算法
基于上面的光滑函数,我们提出一种新的牛顿算法:令dk=(△μk,△xk),定义模函数θ:R++×Rn→R+:
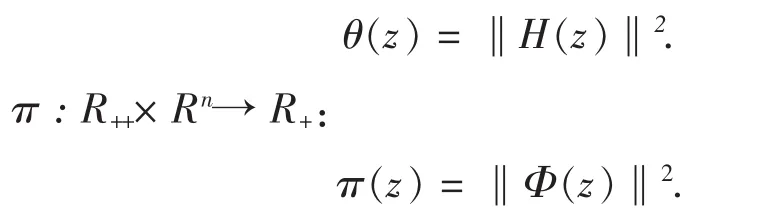
我们现在提出求解问题(1.1)的一个光滑牛顿法。
算法3.1(光滑牛顿法)
步0选取参数δ∈(0,1),η>0,σ∈(0,1/2),置z0:=(μ0,x0)∈R++×Rn为任意点.
步1如果‖Φ(xk)‖=0,停算;
步2解下面方程组得dk

置tk:=δm,z軇=(μ軌k,x軇k):=zk+tkdk,这里m为使下式成立的最小非负整数,
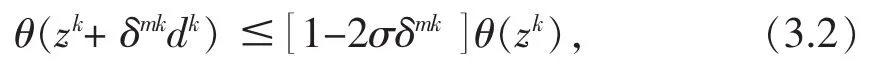
如果tk=1,则令zk+1:=z軇k,k:=k+1转到步骤1.否则转到步骤3
步3如果‖Φ(μ軌k,x軇k)‖燮η μ軌k成立,则令zk+1:=z軇k,k:=k+1转到步骤1.
步4否则,求△x軇k满足
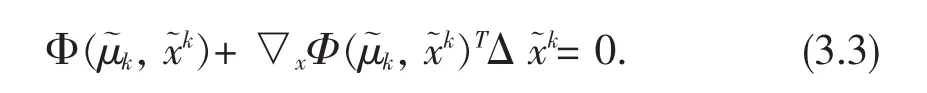
置x軇k:=x軇k+δl△x軇k转到步骤3,这里l是使下式成立的最小非负整数,
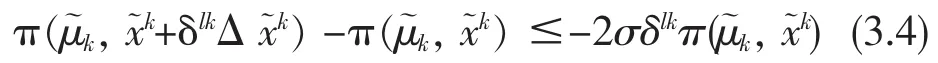
注3.1由式(2.9)、(2.11)的形式知,由式(3.1)求dk的方法可以分成两步:第一步是求△μk使得下式成立:

第二步是解n维线性方程得到△xk.
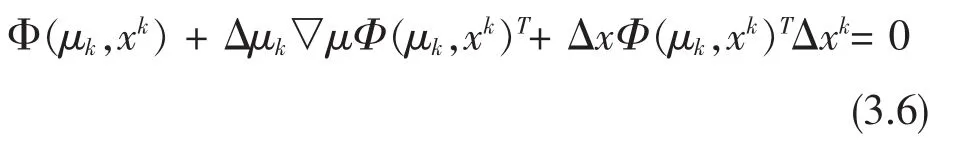
下面我们来证明这个算法是适定的。为此,我们引出如下假设:
假设3.1水平集D0={z∈R+×Rn|θ(z)燮θ(z0)}有界。
引理3.1{μk}单调下降,且μk>0对所有的k成立。证明:由(3.5)可得又由可知△μk>-μk.同时我们知道0
如下的定理表明算法3.1中的步骤2和步骤4是有限终止的。
证明:只需要证步骤2是有限终止的,步骤4同理可证。
由于f,ek-1均是光滑的知H在μ>0时是光滑的。因此θ是光滑函数。我们有
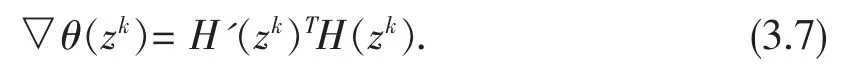
用反证法证明。假设步骤2中的线搜索不是有限终止的,则由(3.2)有
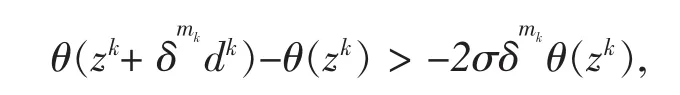

对于任意mk都成立。上式两边除以δmk且令mk→∞,就可以得到由(3.1),(3.7),(3.8)可得也即是但是≠0且
定理3.2算法3.1中的步骤3和4的迭代有限终止。
k调下降且趋于0.因此,对于充分大的l有不等式‖Φ(μ軌,~xki)‖燮η μ軌成立。
kk
§4全局收敛性分析
下面证明算法3.1的全局收敛性。由定理1知算法3.1产生无限序列我们将证明迭代序列的任一聚点都是非线性方程组(2.10)的解。
定理4.1设H:R+×Rn→Rn+1是由(2.9)定义的函数。假设假设条件3.1成立。则算法3.1要么有限终止于‖Φ(x)‖=0的一个解,要么生成一个无限数列这个序列的任意一个收敛点中的x*都满足
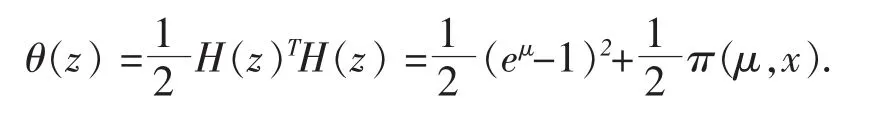
由算法3.1的更新规则知{θ(zk)}是单调下降的。因此由假设3.1,{zk}存在一个收敛点
当tk=1时,由(3.2)有因此,如果步骤2中tk=1无限次发生,则有=0,也即是
下面讨论tk≠1发生有限次的情况。
由引理2.1知对于任意的k有荦H(zk)是非奇异的。同时由假设3.1及θ(zk)是单调下降的可知,存在
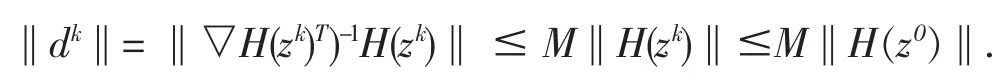
因此对于所有的k,{dk}都有界。
由引理3.1知{μk}单调下降。所以有μk叟μ*.所以有如果则由步骤3中μk的更新规则可以推出μk→-∞.因此,必须有lim in fk→∞tk=0。
令K0是使得序列收敛到0的指标集。不失一般性,我们可以假设序列收敛到z*。由(3.2)有
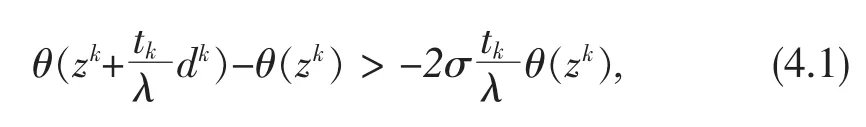
两边同时除以tk,且取极限,有
λ
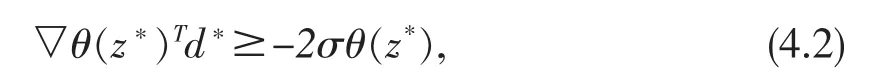
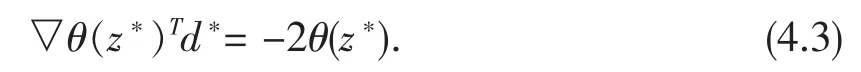
§5数值例子
为了验证算法3.1的有效性,我们对几个问题进行了数值实验,并就迭代次数与非精确N e w to n型信赖域算法(以下简称算法N T)和非精确L e v e n b e rg-M a rq u rt型信赖域算法(简称算法L-M)进行了比较(参见[12]),数值结果如以下诸表。在下列各实验中,迭代次数右上角打*号的表示收敛到退化解,迭代次数打*号的表示算法的迭代次数超过100次。
算例1[8]试验函数为
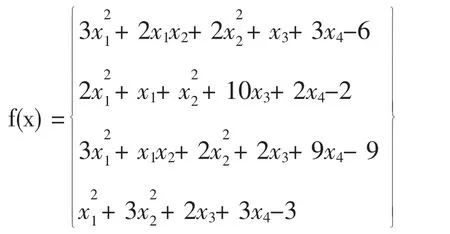
这个例子有一个非退化解(1,0,3,0)T和一个退化解试验中,我们取ρ=0.95,σ
=0.25,α=0.5,λ=0.4,终止值取为θ(xk)<10-12.对于不同的初始值,数值结果如表1.
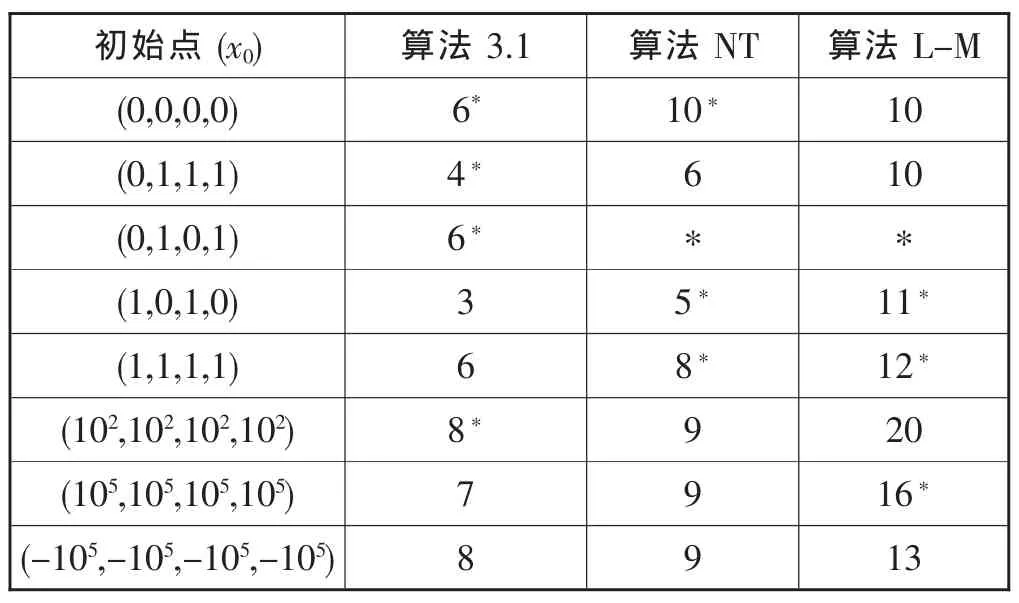
表1算例3.1的数值结果
算例2[11]试验函数为
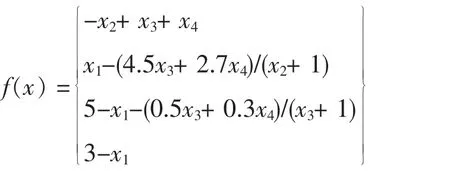
这个例子有无穷多个解x*=(λ,0,0,0)T,其中λ∈[0,3],λ=1,3时为退化解.试验中,我们发现参数ρ的取值对迭代次数较为敏感,对于不同的初始点,我们选取合适的ρ值,其它参数和终止准则值同算例1,数值结果如表2.
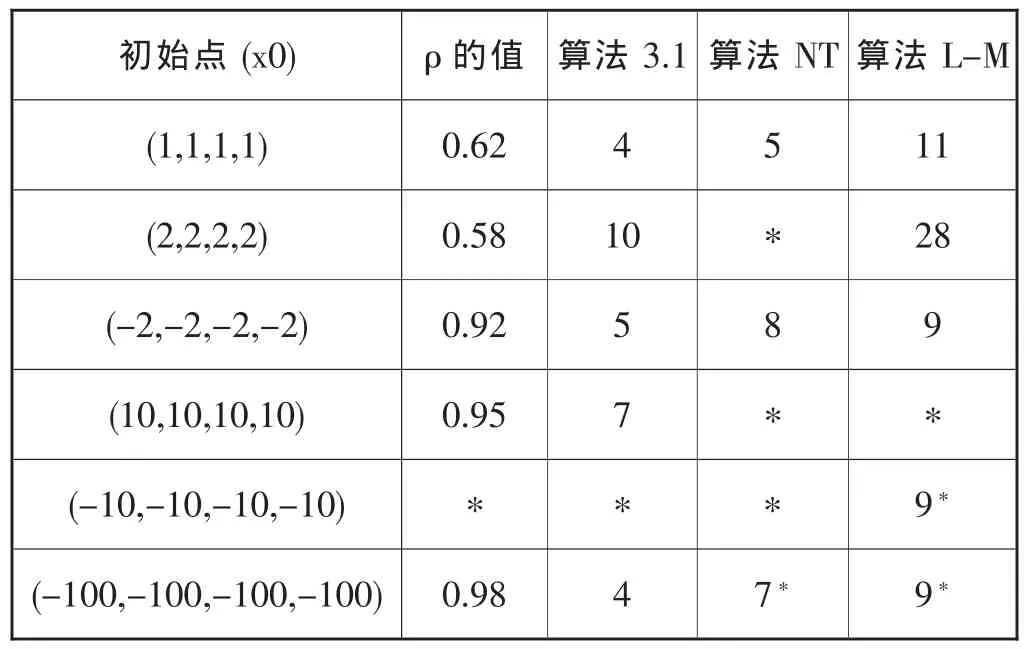
表2算例2的数值结果
§6结论
基于光滑牛顿法思想,本文通过引进一个新的光滑N C P-函数,建立了求解非线性互补问题光滑牛顿法,并在适当的条件下证明了算法的全局收敛性。此外,可以证明在一定的条件下,算法产生的迭代序列至少存在一个聚点,并具有局部二阶收敛速度,这将是我们进一步的工作。
[1]Z h a n g L ip in g,G a o Z iy o u,S u p e rlin e a r/q u a d ra tic o n e-ste p sm o o th in gN e w to nm e th o dfo rP 0-N C Pw ith o u tstric t c o m p le m e n ta rity[J],M a th e m a tic a lM e th o d so fO p e ra tio n R e se a rc h,p p.231-241(2002).
[2]H a rk e r,P.T.,P a n g,J.S.,F in ite-d im e n sio n a l v a ria tio n a l in e q u a litya n dn o n lin e a rc o m p le m e n ta rityp ro b-le m s:A su rv e yo fth e o ry,a lg o rith m sa n da p p lic a tio n s[J], M a th e m a tic a l P ro g ra m m in g 48:161-220(1990).
[3]F e rris,M.C.,P a n g,J.S.,E n g in e e rin ga n de c o n o m ic a p p lic a tio n s o f c o m p le m e n ta rity p ro b le m s[J],S IA M R e v ie w 39:669-713(1997).
[4]F isc h e r,A.,A sp e c ia l N e w to n-ty p e o p tim iza tio n m e th o d[J], O p tim iza tio n 24,269–284(1992).
[5]C h e n,B.,a n d H a rk e r,P.T.,S m o o th in g a p p ro x im a tio n s to n o n lin e a rc o m p le m e n ta rityp ro b le m s[J],S IA M Jo u rn a lo n O p tim iza tio n,7(1):403-420(1997).
[6]Q i,H.,Are g u la rize dsm o o th in gN e w to nm e th o dfo r b o x c o n stra in e d v a ria tio n a l in e q u a lity p ro b le m s w ith P 0-fu n c tio n s [J],S IA M Jo u rn a l o n O p tim iza tio n,10(1):315-330(2000).
[7]Q i,L.,S u n,D.,a n dZ h o u,G.,An e wlo o ka t sm o o th in g N e w to n m e th o d s fo r n o n lin e a r c o m p le m e n ta rity p ro b le m s a n d b o xc o n stra in e dv a ria tio n a lin e q u a lityp ro b le m s[J], M a th e m a tic a l P ro g ra m m in g,87(1):1-35(2000).
[8]M a,C.,C h e n,X.,T h e c o n v e rg e n c e o f a o n e-ste p sm o o th in g N e w to n m e th o d fo r P 0-N C P b a se d o n a n e w sm o o th in g N C P-fu n c tio n[J],Jo u rn a lo fC o m p u ta tio n a la n dA p p lie d M a th e m a tic s,216(1):1-13(2008)8.
A G lo b a lly C o n v e r g e n t S m o o th in g M e th o d fo r S o lv in g N o n lin e a r c o m p le m e n ta r ity P r o b le m
H E C h a n
(M a th e m a tic s a n d C o m p u te r D e p a rtm e n t o f W u y i U n iv e rsity,W u y ish a n,F u jia n 3543 00)
T h e n o n lin e a r c o m p le m e n ta rity p ro b le m(d e n o te b y N C P(F))c a n b e re fo r-m u la te d a s th e so lu tio n o f a n o n sm o o th sy ste m o f eq u a tio n s.B y in tro d u c in g a sm o o th in g N C P-fu n c tio n[8]b a se d o n F isc h e r-B u rm e iste r fu n c tio n,th e p ro b le m is a p p ro x im a te d b y a fa m ily o f p a ra m e te rize d sm o o th e q u a tio n s.An e w sm o o th in g N e w to n m e th o d is p ro p o se d fo r so lv in g th e n o n lin e a r c o m p le m e n ta rity p ro b le mw ith P 0 fu n c tio n b a se d o n th e sm o o th in g N C P-fu n c tio n,a n d it n e v e r re q u ire s a p ro c e d u re to d e c re a se a n a p p ro x im a tio n p a ra m e te r.T h e p ro p o se d a lg o rith m is p ro v e d to b e c o n v e rg e n t g lo b a lly.S o m e n u m e ric a l e x p e rim e n ts a re re p o rte d.
n o n lin e a r c o m p le m e n ta rity p ro b le m;sm o o th in g N e w to n m e th o d;g lo b a l c o n v e r-g e n c e
book=2,ebook=1
O 224.2
A
1674-2109(2011)02-0035-05
2011-02-10
2009年武夷学院科研基金资助项目(项目编号:x q 0927)。
何婵(1984-),女,汉族,助教,主要研究方向:性互补问题的算法。
