太阳能路灯光电板气动导风设计数值研究

花长城，彭兴黔

(华侨大学土木工程学院，福建 泉州 362021)

目前，城市夜景照明广泛应用光电技术及LED新技术，利用倾斜放置的太阳能光电板在白天吸收并贮存太阳热能，夜间将其转换成电能发电，供街道、广场等公共场所的LED照明使用。太阳能光电板是主要的吸热换电器件，因其露天设置于电杆上，对风荷载较为敏感，尤其在我国东南沿海地区，因其自重较轻，常在台风作用下发生损坏，造成较大的经济损失，同时其被风毁堕落也可能造成行人伤亡事故，因此抗风设计已成为光电板结构设计的关键。历次灾害调查表明，单纯采用加强构件和连接措施并不能有效解决结构的风致损坏问题，因此国内外已有学者采取气动措施来控制结构的风致损坏。FRANCHINI［1］等对一低矮房屋弧形屋面做了腾空悬挑女儿墙处理，风洞实验表明这种女儿墙可以有效地降低弧形屋面负压峰值。BANKS［2］对50%开孔率(圆孔)的透风女儿墙做了风洞实验，发现负压峰值可减小50%左右。傅继阳［3］等提出在悬挑屋盖承受较大负压的屋檐和角点附近部位采取开槽气动措施，可有效削减屋盖风敏感处的风荷载值。黄鹏和顾明［4］研究了悬挑屋盖结构在顶部开洞情况下屋盖表面的风压分布特性，结果表明开洞后屋盖上的风压有一定程度的降低。结合前人研究成果，笔者提出以气动措施导风设计方法来疏导光电板表面的风荷载，以期有效地解决光电板风致损坏问题。

1 数值风洞模型

1.1 模型及计算工况

笔者根据光电板及其导风板的实际尺寸建立几何实体模型，根据文献［5-6］，数值风洞计算域的长、宽、高分别取120 m、100 m、60 m，光电板处于流域沿来流方向的前1/3处。模型的阻塞率为0.013%满足小于3%的要求［7］。计算域的离散采用适应性较好的四面体非结构化网格，模型面上的网格尺度为0.01 m。根据文献［8-10］，数值模拟时选取SST k-ω模型，1.75阶迎风格式，迭代残差小于0.0001时认为计算收敛，经过计算收敛性较好。

笔者算例的太阳能光电板是厚度较小的矩形板，与水平方向夹角 β=24°(闽南地区一般取值)，距地面高度H=11 m，底边长L=1 m，斜边宽B=0.8 m，如图1所示。根据研究对象的特性和对称性，笔者选用了7个风向角，导风板的布置及来流风向角的定义如图2所示，取角度α=90°-β=66°(即导风板竖直)和90°(即与光电板垂直)，导风板高度为h，导风板设置状况以h/B表示，分别取h/B=0(即未加导风板)和h/B=0.1、0.2、0.3、0.4。考虑63种工况，在每种工况下研究光电板的风压分布。

图1 光电板照片

图2 加设导风板和风向角位置示意图

1.2 湍流模型和边界条件

入口风剖面为:

湍流强度为:

式中:u1为垂直高度z位置的水平风速;u0为参考高度z0处的风速，取z0=10 m，u0=5.35 m/s;该建筑所处地面粗糙度为B类，粗糙度系数α取0.16，对应的梯度风高度zG=350 m。

湍流动能为［11］:

湍流积分尺度为［12］:

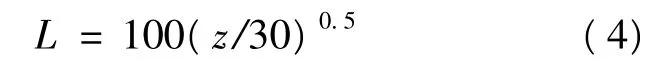
耗散率为:

式中:z为建筑物的高度;常数C=0.09;卡曼常数K=0.41。

出口面假设湍流已充分发展，地面、建筑物表面采用非滑移壁面，在近壁面区采用壁面函数法［13］，数值风洞边界采用自由滑移壁面。

2 气动导风设计结果分析

2.1 各种工况下光电板的净风压

光电板的平均风压系数定义为Cp，为各计算点的风压系数Cpi按该点所属面积Ai的加权平均值，其计算式为［14］:

但在实际应用中，一般采用面上的净风压系数，即用上下表面的平均风压系数之差来表示光电板的净风压系数ΔCp，即:

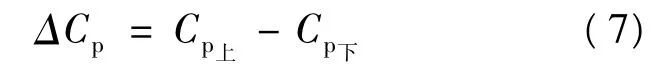
笔者给出的平均净风压系数ΔCp均以B类地貌10 m高度处的风压为参考风压。

带导风板时的光电板净风压系数曲线如图3所示。从图3可以看出:当在光电板的边缘处设置导风板时，可以减少风荷载在光电板表面的附着。如图3(a)所示导风板竖直时，随着导风板高度的增加，光电板表面的净风压系数减小，风向角为90°时，由于来流与导风板平行，因此光电板净风压系数几乎没有减小。导风板相对高度h/B=0.3和0.4时，卸载效果最为显著，光电板上最大净风压系数为0.4左右。此时由于光电板上的净风压系数几乎相同，因此没有继续增加导风板的高度。如图3(b)所示导风板与光电板垂直时，基本变化规律与前者相类似，当导风板相对高度h/B=0.4时，卸载效果最为显著。由图3(a)与图3(b)比较可知，在任意风向角下，导风板都具有一定的卸载效果，即使在最不利的0°和180°风向角下，卸载效果也较为显著，导风板竖直放置时，卸载效果较导风板与光电板垂直放置要好。随导风板高度增加，卸载也增加，当然，导风板自身也受风荷载作用，在设置导风板时应优化其设计高度。

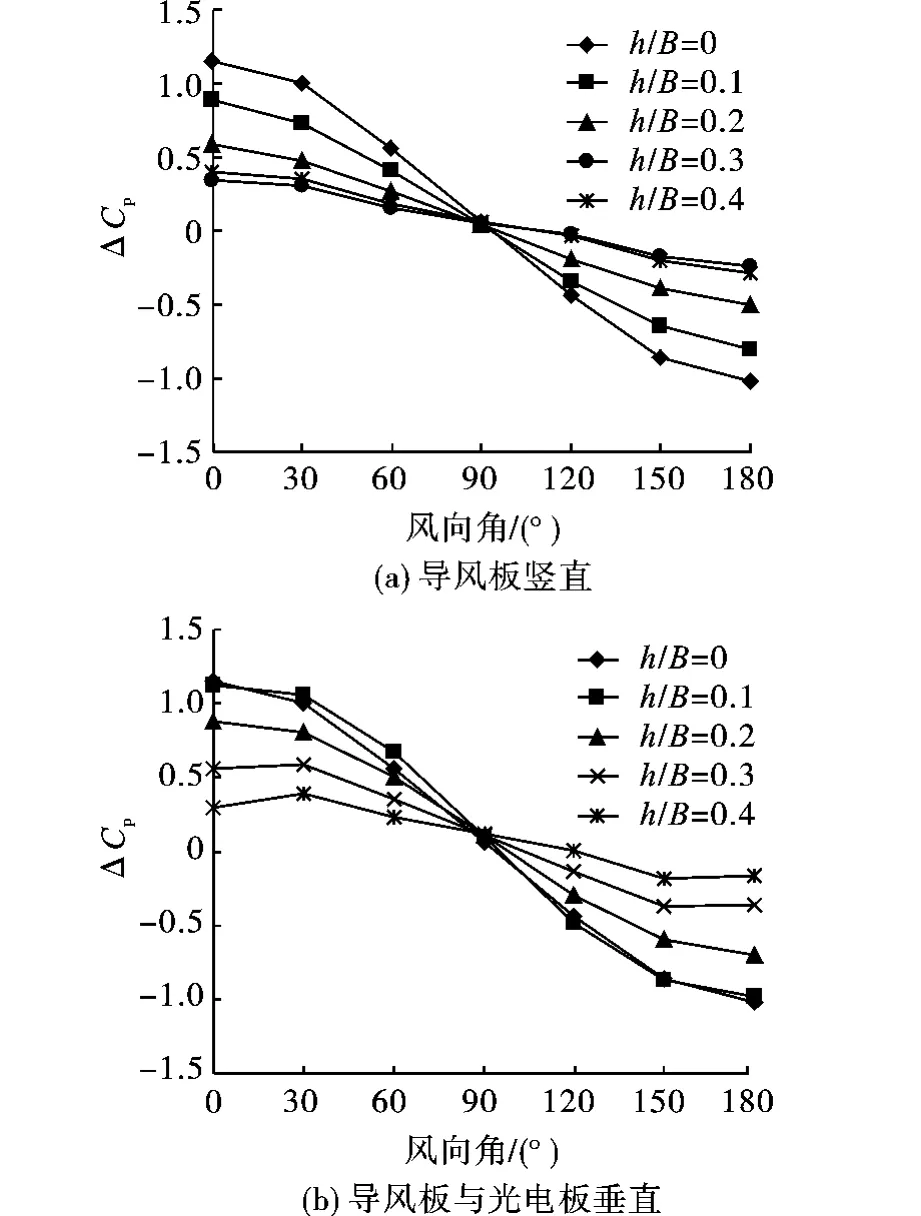
图3 带导风板时的光电板净风压系数曲线

2.2 光电板的减压率分析

为了比较光电板减压的效果，定义光电板的减压率为:

式中:ΔCp0j为没有导风板时j风向角的净风压系数(j为风向角变化);ΔCpij为对应j风向角和导风板i高度时光电板净风压系数(i为导风板高度的变化)。具体计算结果如表1所示。总体来说，随着导风板高度的增加，光电板的减压率也逐渐增加。在同等条件下，导风板竖直设置时光电板的减压率比导风板与光电板垂直设置时好。综合考虑最优的导风板设置取导风板竖直安放、相对高度h/B=0.2，此时减压率可以达到50%。减压效果显著。

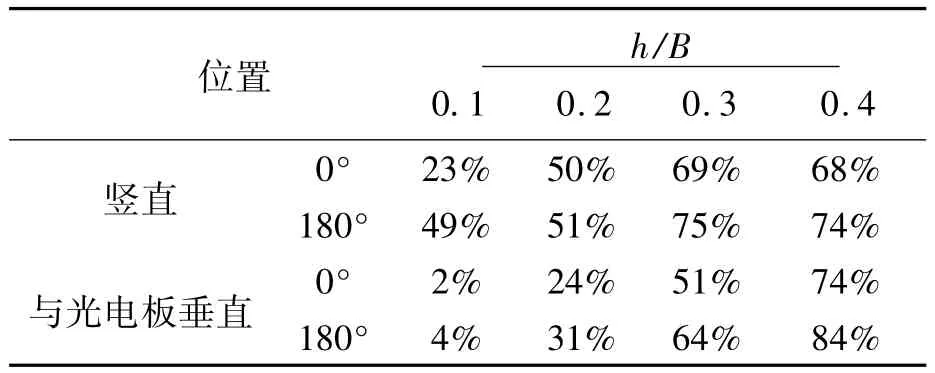
表1 光电板在不同高度和角度导风板下的减压率

2.3 减压机理比较

为了进一步理解光电板的减压机理，探讨其内在规律，笔者选取了导风板设置的最优值和未设置导风板的光电板在0°风向角下的附近流场进行对比分析，如图4所示。由图4(a)可以看出，来流直接作用在光电板上，光电板上表面风荷载较大且风力分布较均匀，在光电板边缘分离处风速突然增大，下表面风荷载低于上表面以吸力为主。图4(b)因导风板的设置，改变了光电板周围的空气流场，减少了风荷载在光电板上表面的附着面积，减轻了气流对太阳能光电板上表面的撞击，即减小了太阳能光电板上表面风压力;同时光电板的设置减轻了气流在光电板下表面的分离，即减小了太阳能光电板下表面风吸力，从而对太阳能光电板起到减小风荷载的作用。

3 结论

图4 0°风向角下光电板附近的流场图

通过以上分析证明，所提出的变被动抗风设计为主动导风设计的新理念，能有效地疏导光电板表面的风荷载。同时通过对光电板边缘设置不同的导风板进行比较分析，可知导风板的存在可改变太阳能光电板的空气流场，有效减卸高速气流在太阳能光电板上施加的风荷载，保障太阳能光电板安全及其正常使用功能，同时得到导风板设置的最优值，即导风板应竖直且相对高度h/B=0.2，此时减压率约为50%。因此，笔者的研究成果可以为以后沿海地区光电板的抗风设计提供参考。

［1］FRANCHINI S，PINDADO S，MESEGUER J，et al.A parametric，experimental analysis of conical vortices on curved roofs of low-rise buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，2005，93(3):639-650.

［2］BANKS D.The suction induced by conical vortices on low-rise buildings with flat roofs［D］.Fort Collins，Colorado:Department of Civil Engineering，Colorado State University，2000.

［3］傅继阳，甘泉.开槽对大跨悬挑平屋盖结构风荷载的影响［J］.实验力学，2003，18(4):458-465.

［4］黄鹏，顾明.一大跨度悬挑雨篷的风荷载及开洞比较［J］.结构工程师，2004，20(4):51-55.

［5］孙晓颖，武岳，林斌，等.土木工程CFD数值模拟中的参数设置［C］//第七届全国风工程和工业空气动力学学术会议论文集.成都:［s.n.］，2006:558-563.

［6］侯爱波，江梦甫.建筑数值风洞的基础研究［J］.湖南大学学报:自然科学版，2007，34(2):21-24.

［7］MOCHIDA A，ISAAC Y F L.Prediction of wind environment and thermal comfort at pedestrian level in urban area［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96(7):1498-1527.

［8］BEKELE S A，HANGAN H.A comparative investigation of the TTU pressure envelope-numerical versus laboratory and full scale results［J］.Wind and Structures，2002，5(2/4):337-346.

［9］TOMINAGAA Y，MOCHIDAB A，YOSHIE R，et al.AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96(10/11):1749-1761.

［10］曾锴，汪丛军，黄本才，等.计算风工程中几个关键影响因素的分析与建议［J］.空气动力学学报，2007，25(4):504-508.

［11］RICHARTSON G M，HOXEY R P，ROBERTSON A P，et al.The silsoe structures building:comparisons of pressures measured at full scale and in two tunnels［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，85(1):187-197.

［12］AYNSLEY R M.Politics of pedestrian level urban wind control［J］.Building and Environment，1989，24(4):291-295.

［13］陶文锉.数值传热学［M］.2版.西安:西安交通大学出版社，2001:147-165.

［14］黄本才，汪丛军.结构抗风分析原理及应用［M］.2版.上海:同济大学出版社，2008;14-31.