基于自适应动态规划的三容水箱液位控制

傅 剑，陆世辉，李绘英，余 愿

(武汉理工大学自动化学院，湖北 武汉 430070)

三容水箱模型是一个典型的液位控制模型，具有大滞后性、非线性的典型系统特点［1］。目前，对三容水箱系统进行控制的常规方法主要是把非线性系统线性化，使其满足复杂控制系统的性能要求。传统的控制方法最主要有PID控制［2］、预测控制［3］、模糊控制［4-5］和 H∞控制［6］等。然而传统PID控制对于控制对象参数变化无法自适应;预测控制算法主要用于线性系统;模糊控制又受限于设计者和操作人员的经验知识;H∞控制存在系统保守性的问题。总之，这些方法要么受到线性化的限制，要么受到模型的限制。因此笔者考虑采用了自适应动态规则(adaptive dynamic programming，ADP)在线学习算法，其理论基础根植于动态规划的贝尔曼方程，从而在动态过程中取得基于某种性能泛函的最优［7-8］。

ADP使用函数逼近器来近似该性能函数，从而实现学习和控制进而克服传统动态规划的维数灾难问题。简言之，ADP在线学习不依赖于先验知识，而是根据环境反馈的评价信号和环境状态来近似最优控制策略，具有良好的通用性，适合用于处理时变的非线性复杂系统。采用这种方法来控制三容水箱液位，使系统具有较强的自适应能力以克服干扰和系统内部的摄动。

1 三容水箱模型

典型的三容水箱模型［9］如图1所示。

图1 三容水箱模型

三容水箱模型由3个水箱、3个阻力板和1个调节阀组成，在各个水箱的出水口处放置有非线性阻力板。水箱1～水箱3的进水量分别为Qi、Q1、Q2，其中 Qi由调节阀开度 μ 控制;出水量分别为 Q1、Q2、Q3，底面积分别为 F1、F2、F3。

当系统平衡后突然加大流入量Qi，使得液位H1随Qi的增大而变高，又由于Q1与H1相关，因此Q1随之变大;同理，Q1变大后，导致 H2、Q2随之相应变大;最后H3、Q3也随之变大。当H1、H2、H3上升到一定高度后，系统达到新的平衡点或液位过高导致溢出。反之，减少流入量Qi，系统最终平衡在另一个液位上或减少到该层水箱底部。选取状态量 X=(H1，H2，H3)，进水量 Qi为控制量。控制目标是:系统平衡后，当Qi被干扰时，系统呈现不平衡趋势，经过ADP在线学习和控制，最后系统保证3个水箱的液位都在设定范围内。

根据物料平衡推导得出液位数学模型的动态方程组如下:

其中，α(H)为流量系数，它与液位H和阻力板模型有关。

在实际过程中，Qi会受到干扰的影响，因为它是由调节阀的开度来控制，而控制调节阀的电器可能受到电磁干扰或因长期磨损导致其工作曲线偏离出厂的设定值。这里设定干扰为两种，时不变的干扰和时变的干扰，用以检验系统的抗干扰性，进而验证该系统的学习能力和鲁棒性。

阻力板的模型如图2所示。以阻力板1为研究对象，假设水箱1液位下降的速度为V1，大气压力为P，阻力板的液体流出速度为V2，液位为y，根据理想的伯努利方程得:

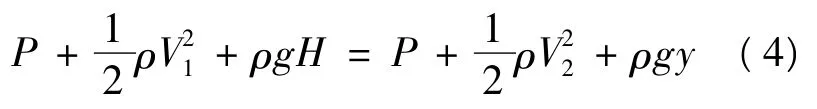
图2 阻力板模型

由于V1＜＜V2可忽略不计，因此式(4)可化简为:

阻力板的流出量Q(H)可以由阻力板的液位面积S乘以速度V2得到，即:

而面积S可以由定积分元素法求出。当水箱液位不同时，可以由下面的积分来求Q(H)的值。

(1)当H≤10时，Q(H)的计算公式为:

(2)当10＜H≤60时，Q(H)的计算公式为:

(3)当60＜H≤70时，Q(H)的计算公式为:

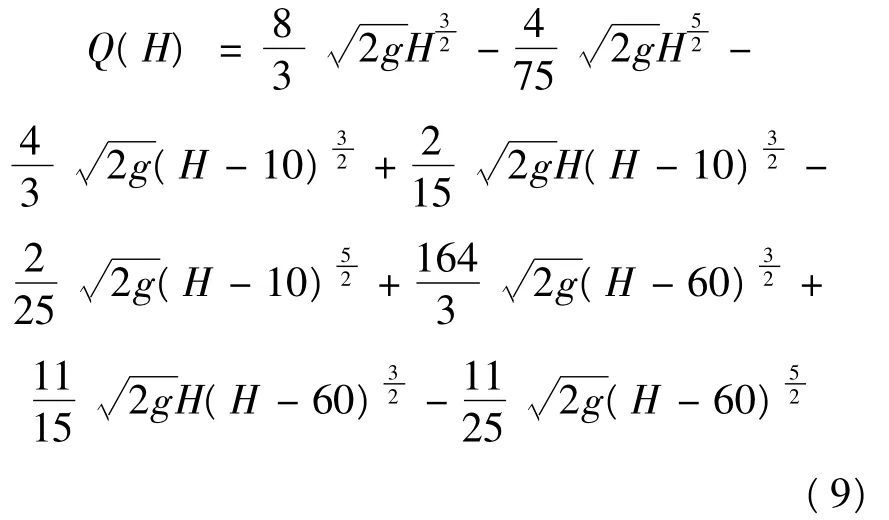
(4)当70＜H≤100时，Q(H)的计算公式为:

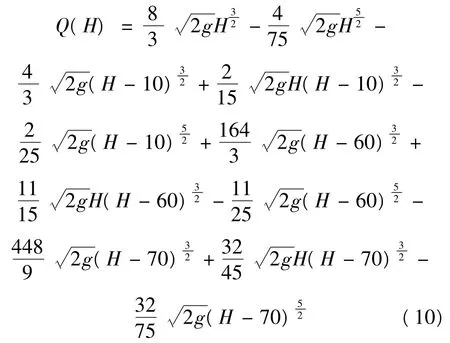
根据文献［9］的实验数据，可以得到流量系数α(H)作为对理想建模假设的修正值为:

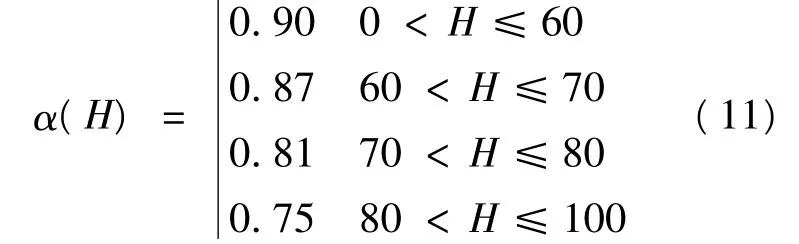
那么由式(1)～式(11)可以得到三容水箱系统的动态方程为:

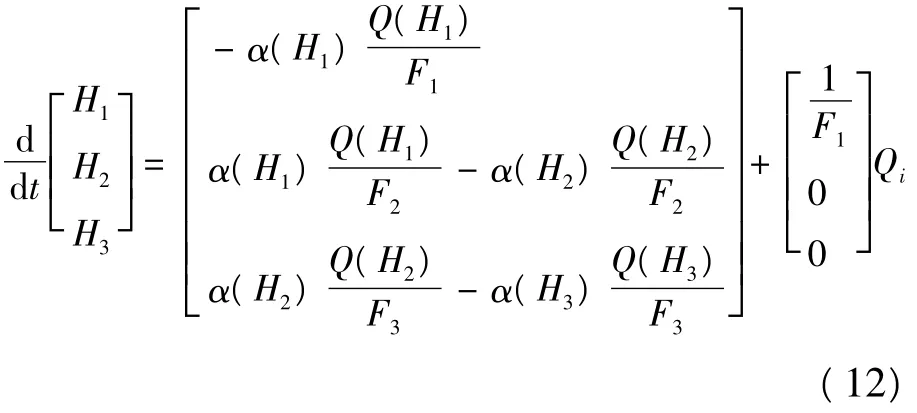
可见式(12)为非线性微分方程，其系数矩阵的元素随着3个水箱液位的不同而变化。

2 ADP的相关理论

2.1 ADP的结构和工作原理

自适应动态规划是动态规划、强化学习和人工神经网络相融合而产生的交叉领域，也可以认为是离散领域的强化学习在连续领域的扩展。自适应动态规划的本质是基于动态规划原理、强化学习原理，模拟人通过环境反馈进行学习，是一种非常接近人脑智能的算法［10］。

ADP的基本思想可以用图3表示。它通常由动态系统、动作控制和评论性能指数函数3个模块组成。其中动作控制和评论性能指数函数组合成为一个Agent。当动作控制模块的输出作用于动态系统后，系统就产生新的状态和奖惩值，评论模块根据获得的状态和奖惩值，来影响动作控制模块。具体来说就是评论值函数的参数更新是基于Bellman最优原理进行的，目标是A动作控制必须使得评论值函数最小。这样就可以通过调整网络的权值来在线响应系统的动态变化。

图3 ADP的原理图

随着研究的深入，人们设计出了很多具体的算法来实现 ADP算法［11］，如 ADHDP(action dependentheuristicdynamicprogramming)、HDP(heuristic dynamic programming)和DHP(dual heuristic dynamic programming)等，笔者采用的是无参考模型的 ADHDP［12］。

ADHDP是由HDP发展而来的，它比HDP少了一个模型网络，因此不需要知道系统的动态模型即可实施控制，这是其非常显著的一个优点，因为在实际系统中，常常很难或无法得到控制对象的控制模型而要去实施控制。具体到三容水箱这种场合，整个系统由行为网络、评价网络和三容水箱模型组成。需要特别指出的是三容水箱模型仅仅是为了模拟环境对象本身，对于ADHDP而言是不知道其模型也不需要其模型结构即可实施控制。状态X(t)为行为网络的输入，行为网络的输出为u(t)，u(t)和X(t)一起作为评价网络的输入，J(t)为评价网络的输出，J(t-1)为上一时刻评价网络的输出值，Uc(t)为行为网络的期望值，r(t)为奖惩值，成功时为0，失败时为-1;α为折扣因子。三容水箱系统结构图如图4所示。

系统学习控制过程的伪代码描述如下:

while 终止条件do

图4 三容水箱系统结构图

初始化状态X行为网络权值Wa评价网络权值Wc

repeat

计算行为网络的输出u

通过三容水箱系统得到新的状态X和及时奖惩值r

基于时序差分计算cost-to-go的误差Ec

采用反向传播算法训练评价网络使误差Ec最小

采用反向传播算法，通过调整行为网络的权值，使得‖J-Uc‖最小。

until当前状态不属于液位范围end while

2.2 在线学习算法

在设计中，行为网络和评价网络都是非线性的多层前馈网络。具体的神经网络结构如图5所示。

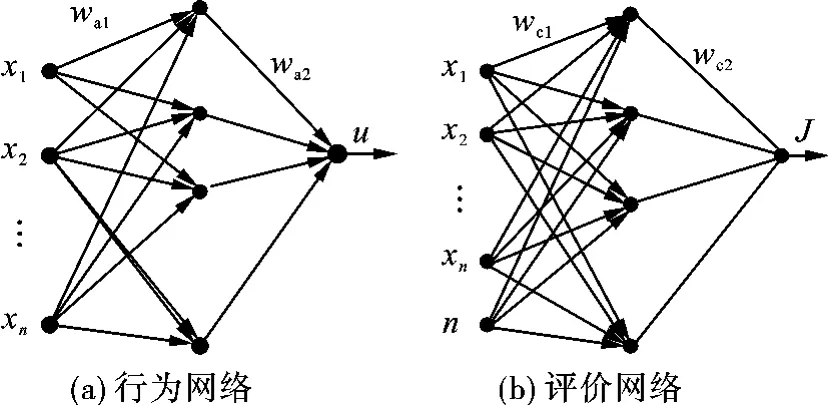
图5 行为网络和评价网络的结构图

2.2.1 行为网络

行为网络的误差值为ea(t)，Ea为行为网络的均方差，目标是使Ea最小。

由图5可以得到行为网络的输出为:

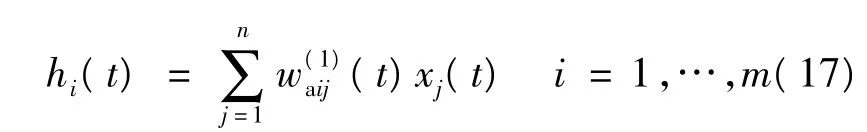
式中:hi为神经网络第i个隐层节点的输入;gi为神经网络的第i个隐层节点的输出;m为隐层节点数;n为神经网络输入量的个数。

行为网络权值的更新公式为:

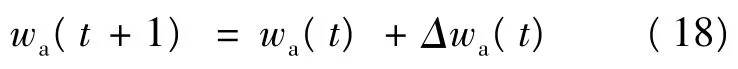
从输入到隐层的权值变化量为:

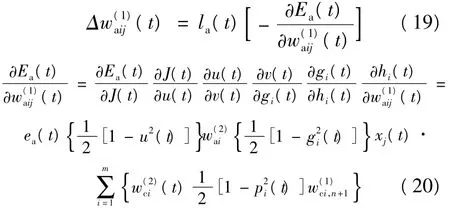
从隐层到输出的权值变化量为:

其中，la(t)＞0为神经网络在t时刻的学习率，它随着时间的递增而减小。

2.2.2 评价网络

评价网络的目标函数为均方差Ec，其目标是使目标函数最小，其思想来源于动态规划的最优化原理和嵌入原理。

根据图5可得评价网络的输出函数J(t)为:

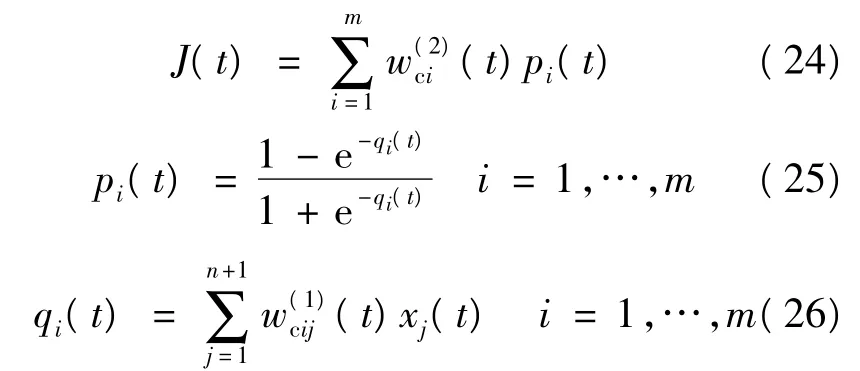
式中:qi为神经网络的第i个隐层节点的输入;pi为神经网络的第i个隐层节点的输出;m为隐层节点数;n+1为神经网络的输入变量的个数。

评价网络的权值更新公式为:

从输入层到隐层的权值变化量为:

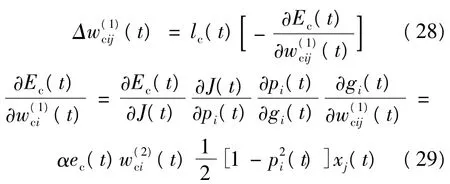
从隐层到输出层的权值变化量为:

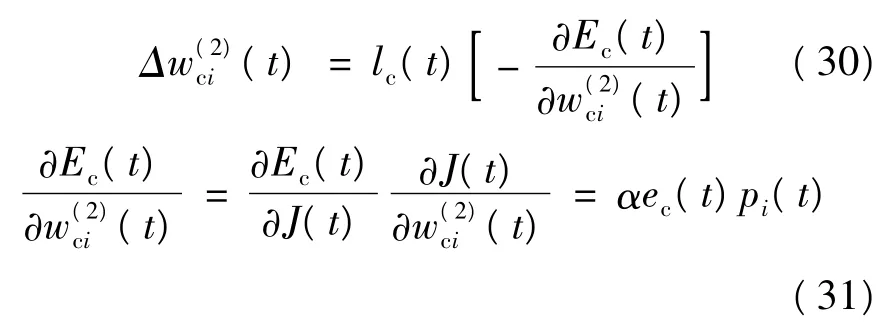
3 仿真及结果

3.1 设定参数

水箱的底面积F1=166585 mm2，F2=169510 mm2，F3=166585 mm2，g=9806.65。

行为网络输入节点n=3，隐层节点m=10;评价网络输入节点n=4，隐层节点m=10;初始学习率la=lc=0.3，每5个时间步减少0.005，直到≤0.005为止;行为网络和评价网络内部训练误差的阈值Ta=0.005，Tc=0.05;折扣因子α=0.95;取时间步为0.02 s。

取控制量Qi=98000 mm3/s;状态量H1=H2=H3=65 mm;水位波动最大值boundary=2 mm;希望奖惩值Uc=0。

在一次运行过程中，有20次训练。当加入干扰后，要求成功的训练序号在20以内，并且在该次训练过程中，实时的在线学习和控制使得3个水箱的液位控制在［63，67］之间，并且至少持续6000个时间步，即120 s。

3.2 仿真结果及分析

当给控制量Qi施加0.25 sin(2π·0.03 t)干扰时，获得3个水箱的液位曲线图，如图6～图8所示。可见，当第一次训练到187步时，H1低于设定的液位下限63 mm(H2、H3在设定范围内)，训练失败;第二次训练到724步时，H1低于设定的液位下限63 mm(H2、H3在设定范围内)，训练失败;第三次训练成功地进行了6000个时间步，且3个水箱的液位都在［63，67］范围内，训练成功。图9为训练成功时进水量Qi的曲线图。

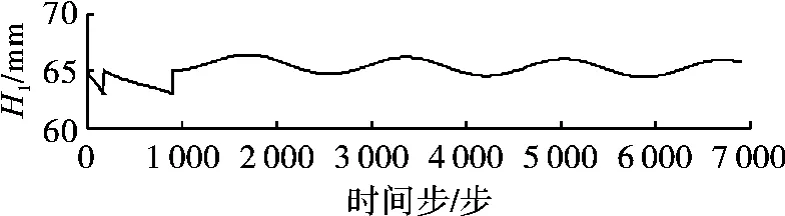
图6 液位H1的曲线图

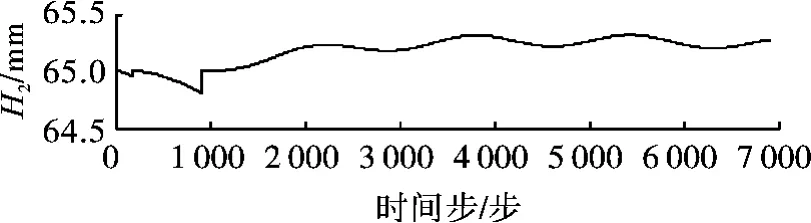
图7 液位H2的曲线图

图8 液位H3的曲线图

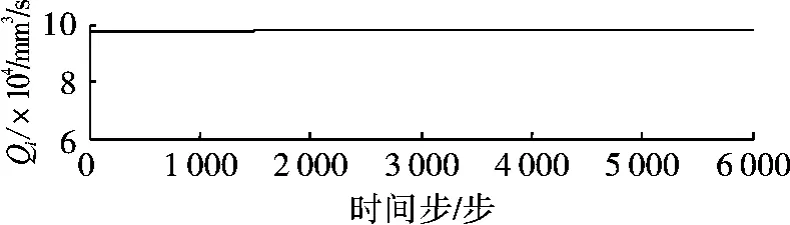
图9 流入量Q1的曲线图

当不同类型的干扰施加于控制量Qi时，比较ADHDP在各种干扰条件下对系统在线学习和控制的能力。设定每种干扰下进行30个训练过程，每个过程有20次训练，每次训练有6000个时间步。仿真结果如表1所示。

表1 性能比较

从表1可以看出，虽然有不同的干扰叠加在三容水箱的进水阀上，ADHDP有很强的学习能力很快适应了这种变化，从而实施了有效的控制。

4 结论

首先建立了三容水箱的数学模型，然后引入ADP的无参考模型的ADHDP结构，直接对三容水箱非线性系统本身实施在线学习和控制。Matlab仿真实验验证了该方法的正确性和可行性。经过分析仿真结果发现，采用ADP在线学习来控制三容水箱系统，有较好的控制效果和鲁棒性。

［1］金以慧.过程控制［M］.北京:清华大学出版社，1993:8-15.

［2］李智，张雅婕，杨洁.基于实验的三容水箱数学模型［J］.武汉工程职业技术学院学报，2009，21(3):1-4.

［3］谢启，杨马英，余文正.基于预测函数控制算法的水槽液位控制系统［J］.控制工程，2003，10(6):509-511.

［4］李学军，徐俊山.三容模糊控制系统设计［J］.长春大学学报，2004，14(6):8-10.

［5］朱海荣，杨奕，姜平，等.三容系统的智能神经网络模糊控制研究［J］.电气传动，2007，7(7):46-49.

［6］韩光信，张桂芹，施云贵.三容系统H∞控制［J］.吉林化工学院学报，2004，21(4):37-39.

［7］BELLMAN R，DREYFUS S.Applied dynamic programming princeton［M］.NJ:Princeton Univ Press，1962:25-50.

［8］WANG F Y，ZHANG H G，LIU D R.Adaptive dynamic programming:an introduction［J］.IEEE Computational Intelligence Magazine，2009，8(3):39-47.

［9］赵科，王生铁，张计科.三容水箱的机理建模［J］.控制工程，2006，13(6):521-525.

［10］PROKHOROV D V，WUNSCH D C.Adaptive critic design［J］.IEEE Transactions on Neural Networks ，1997，8(5):997-1006.

［11］SI J，WANG Y T.On-line learning control by association and reinforcement［J］.IEEE Transactions on Neural Networks，2001，12(2):264-276.

［12］MURRAY J J，COX C J，LENDARIS G G.Adaptive dynamic programming［J］.IEEE Transactions on Systems，Man，and Cybernetics-Part C:Applications and Reviews，2002，32(2):140-152.