一种新型移动机器人运动学坐标系快速构建方法研究

宋孟军 张明路 张建华

河北工业大学，天津，300130

0 引言

在对串联机器人进行运动学求解的过程中，需要建立机器人的运动学坐标系。传统的构建方法是依据D－H参数法则将坐标系建立在机器人的转动或移动关节处，然后在此基础上应用相应的坐标系变换法则进行相应的坐标系构建[1－4]。这种方法在某些情况下影响了坐标系构建的多样性，且给结构多样的串联机器人的分析工作带来过多的分析步骤，不仅影响了串联机器人设计的效率，而且可能在某种程度上给后续的分析工作带来一定的困难（如存在机器人机构模型不一致的现象从而给分析工作带来困难）。针对这个问题，本文提出冗余坐标系的概念以解决串联机器人运动学坐标系快速构建的问题，从而为串联机器人坐标系的快速构建提供一种新的解决方案；同时沿Y轴进行坐标变换，进一步提高机器人运动学模型构建的效率。构建冗余坐标系及沿Y轴构建运动学模型，两种方法均可提高机器人运动学坐标系构建的效率。

1 D－H法则坐标系的构建

首先，应用D－H 法则[5－6]对一种多足移动机器人的腿部构建全局坐标系，如图1所示，其中连杆参数和关节变量如表1所示。

图1 基于D－H法则构建坐标系

表1 基于D－H法则连杆及关节变量参数

依据运动学方程求解公式可以求出多足机器人末端坐标系相对于固定参考系的位姿解。求解运动学方程，所得位姿解具体情况如表2所示。其中，c1＝cosθ1，s1＝sinθ1，c12＝cos（θ1＋θ2），s12＝sin（θ1＋θ2），余同。

表2 新型移动机器人位姿

2 冗余坐标系的构建

冗余坐标系就是建立在机器人非运动关节处，为机器人整体运动学坐标系的构建起到过渡作用的坐标系，在机器人进行运动时，冗余坐标系并不参与相应的运动（如移动或转动），即冗余坐标系的变换始终为常量。

冗余坐标系的构建仍以本例多足移动机器人为研究对象。首先构建图2所示全局坐标系。

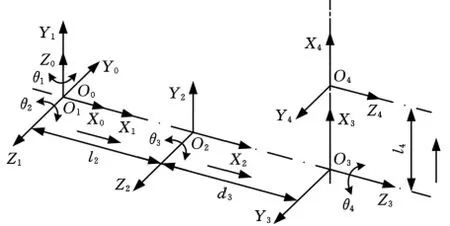
图2 全局坐标系构建

仍依据图1所示坐标系构建方法对多足移动机器人的坐标系进行构建，将基座固定坐标系O0X0Y0Z0通过连杆坐标系进行传递，同时推导末端坐标系O4X4Y4Z4的位姿形态，推导结果如表3所示。

表3 全局坐标系的连杆及关节参数

推导进行到坐标系O3X3Y3Z3时，再依据D－H坐标系的确定方法很难将坐标系O3X3Y3Z3变换到坐标系O4X4Y4Z4，因此本文将采用构建冗余坐标系的方法，在冗余坐标系概念基础上，构建图3所示的全局坐标系。

图3 冗余坐标系构建图

如图3所示，在图2所构建的坐标系的基础上，在原关节3的位置（O2X2Y2Z2）构建冗余坐标系O3X3Y3Z3，从而在表3推导结果的基础上继续对末端坐标系的位姿进行推导，推导结果如表4所示。

表4 冗余坐标系的连杆及关节参数

由表4可以看出，每增加一个冗余坐标系就会增加一个坐标系的传递过程（即推导过程）。与表1所示传递推导过程相比较，冗余坐标系的构建简化了全局坐标系变换的规则，改变了变换的思路，从而有利于快速构建运动学全局坐标系，并且为较复杂的关节变换关系提供了良好的解决方案，有利于构建具有复杂关节变换关系的坐标系系统。

对全局坐标系下的各个变换矩阵进行求解[4]，可以求得上述各个传递推导过程的变换矩阵分别如下：

可以看出，增加了冗余坐标系的变换矩阵与没有增加冗余坐标系的变换矩阵相比，变换矩阵的结构得到了简化，从而便于分析计算。

利用已经求得的各个变换矩阵A1～A5，可以首先得出运动学方程T5：

进而求得运动学方程的正解如表5所示。

表5 新型移动机器人冗余坐标系下位姿

如图1、图3所示，在两种建立全局坐标系的方法中，基坐标系所选择的姿态均相同，而末端姿态略有不同，图3建立的末端坐标系O5X5Y5Z5与图1建立的末端坐标系O4X4Y4Z4，其姿态解并不完全相同，需进行相应的旋转变换，如图4所示。

图4 末端坐标系构建图

由图4可以看出，经过变换后的末端坐标系与图1构建的坐标系具有相同的位姿解。在表2的基础上继续对坐标系O6X6Y6Z6在基座固定坐标系中的位置姿态进行推导，结果如表6所示。

表6 末端连杆及关节参数

表6所示传递过程的变换矩阵可表示为

在变换矩阵A6的基础上，可以得到运动学方程：

同理，可以求得运动学方程T6的正解如表7所示。表7所列θ5与表2所列θ4为同一关节转角变量，即｜θ5｜＝｜θ4｜，而在各自的全局坐标系中，两变量所在坐标系的Z轴相互夹角为180°。当－θ5＝θ4时，将表2所得结果与表7所得结果进行比较可知，两坐标系末端具有相同的位姿正解。

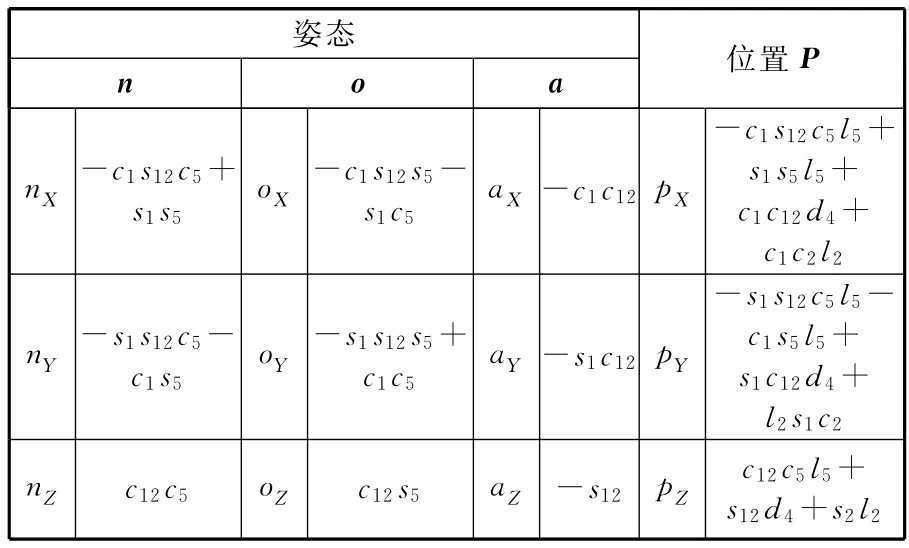
表7 基于冗余坐标系的机器人位姿

3 冗余坐标系的仿真验证

由前面分析可知，应用冗余坐标系构建坐标系所得的位姿结果与应用D－H法则构建坐标系所得位姿结果一致，如表2和表7所示。由表2和表5可知，若两种方法所得末端坐标系不进行相应的转换，则结果并不相同（图5）。图5所示为各个关节变量以不同的非线性函数进行输入时的情况（对正解随机输入的情况进行模拟）。

图5 各关节角度输入情况

应用D－H法则构建的坐标系下，各关节变量输入如图5所示，所得末端坐标系的空间运动轨迹点的X、Y、Z坐标在平面上的投影如图6所示。

在应用冗余坐标系构建方法所构建的坐标系下，各关节变量输入如图5所示，所得末端坐标系的空间运动轨迹在平面内的投影如图7所示。

由图6和图7可知，由于构建坐标系的方法不同，导致部分关节转角的旋向并不相同。将θ5逆向旋转，如图8所示。将图8所示角度应用到冗余坐标系构建方法中，所得结果与图6所示结果相一致。这也进一步证明了冗余坐标系建立的正确性。

图6 D－H法则坐标系末端轨迹投影输出情况

图7 冗余坐标系末端轨迹投影输出情况

图8 θ5变换后各关节角度输入情况

4 沿Y轴构建坐标系

沿Y轴构建坐标系，仍以本例多足移动机器人为研究对象。

依据图1所示坐标系构建方法对多足移动机器人的坐标系进行构建，将基座固定坐标系O0X0Y0Z0通过连杆坐标系进行传递，仍对末端坐标系O4X4Y4Z4的位姿形态进行推导，推导结果如表8所示。

表8 前两关节变换的连杆及关节参数

推导进行到坐标系O3X3Y3Z3时，仍依据D－H坐标系变换方法将坐标系O3X3Y3Z3变换到坐标系O4X4Y4Z4会存在一定的困难。本文将继续分析坐标变换规则，采用将运动学坐标系沿Y轴进行变换的方法，构建图9所示的全局坐标系。

图9 应用坐标变换规则构建全局坐标系

如图9所示，在图1所构建的坐标系的基础上，将关节3处坐标系O2X2Y2Z2变换到关节4处坐标系O3X3Y3Z3，沿Y轴进行旋转变换。将Z轴直接变换到旋转关节4处，这样便减少了变换步骤。如图1所示，将关节3变换到关节4处须进行两次旋转变换，增加了变换的步骤。利用图9所示方法对末端坐标系的位姿进行推导，推导结果如表9所示。由表9可知，坐标系变换既绕Z轴进行旋转和平移变换，同时又绕Y轴进行旋转和平移变换。

表9 后两关节变换的连杆及关节参数

下面依据D－H坐标系的确定方法[4]和沿Y轴进行坐标系变换的方法相结合，对全局坐标系下的各个变换矩阵进行求解。由表8、表9和表1可知，两种方法所对应的前两种关节变换矩阵相同，后两种关节变换矩阵不同，上述各个传递过程的变换矩阵如下：

其中，A3Y、A4Y为在Y轴方向进行坐标变换后所得的变换矩阵，与没有添加冗余坐标系的变换矩阵相比，变换矩阵的计算过程得到了进一步简化，即转换步骤得到了一定程度的简化。

利用求得的变换矩阵A1Y～A4Y可以首先计算出运动学方程T4Y：

进而求得运动学方程的正解如表10所示。

表10 沿Y轴变换机器人位姿

如图1和图9所示，两种建立全局坐标系的方法中，基坐标系选择均相同，而末端姿态有所不同，即图9建立的末端坐标系O4X4Y4Z4与图1所建立的末端坐标系O4X4Y4Z4姿态并不完全相同，需进行相应的旋转变换，如表11所示。

表11 末端坐标系变换连杆及关节参数

由表11所进行的变换可知，经过变换后的末端坐标系与图1所构建的末端坐标系具有相同的位姿解，表11所示传递过程的变换矩阵可以表示为

在变换矩阵A5Y的基础上，可以得到运动学方程T5Y：

同理，可以求得运动学方程T5Y的正解如表12所示。

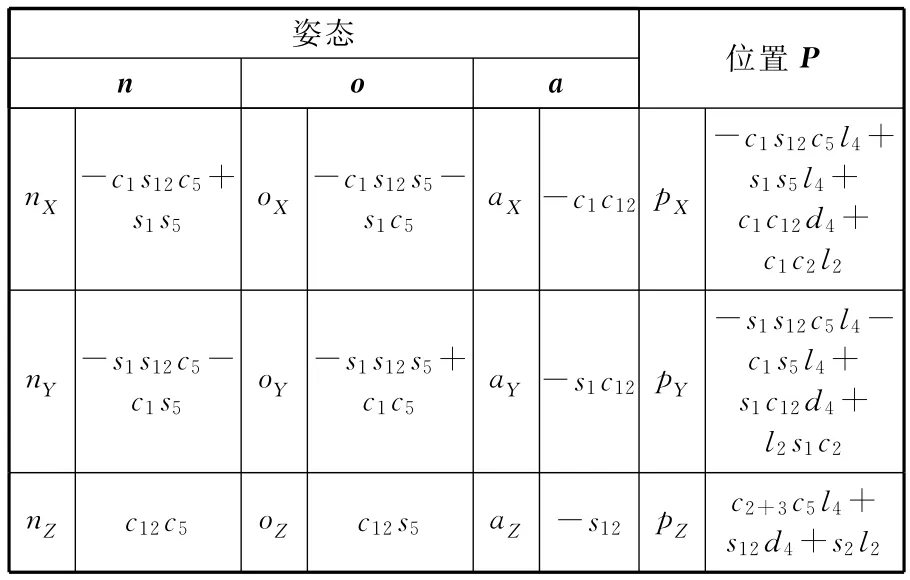
表12 沿Y轴变换机器人最终位姿

表12所列θ5与表2所列θ4为同一关节转角变量，即｜θ5｜＝｜θ4｜，且在各自的全局坐标系中两变量相差180°。当－θ5＝θ4时，表2与表12将具有相同的结果，即两坐标系末端将具有相同的位姿正解。

通过以上求解证明可以发现，沿Y轴进行坐标系变换与使用D－H法则进行坐标系变换，两种方法具有相同的运动学求解结果。

5 结论

本文针对机器人运动学分析过程中坐标系快速构建问题，提出了冗余坐标系的概念，并对冗余坐标系进行了求解，进行了仿真验证，研究结果表明，冗余坐标系的构建可以更加直接、快速地求解机器人的运动学问题，并且可以为运动学求解提供较为准确的运动学模型。

本文进一步沿Y轴进行了坐标变换，构建了多足移动机器人运动学模型，求解了运动学方程，并证明了这种方法的正确性，为快速构建运动学模型、求解运动学方程提出了另一种新的解决方案。

[1]杨峰.JJR－1型机器人运动学分析及其控制系统的研究[D].兰州：兰州理工大学，2006.

[2]陈平.MOTOMAN－UPJ型机器人运动学研究[D].镇江：江苏大学，2006.

[3]张铁，谢存禧.机器人学[M].广州：华南理工大学出版社，2001.

[4]熊有伦，丁汉，刘恩沧.机器人学[M].北京：机械工业出版社，1993.

[5]Tavasoli A，Eghtesad M，Jafarian H.Two－time Scale Control and Observer Design for Trajectory Tracking of Two Cooperating Robot Manipulators Moving a Flexible Beam[J].Robotics and Autonomous Systems，2009，57：212-221.

[6]van Henten E J，Schenk E J，van Willigenburg L G.Collision－free Inverse Kinematics of the Redundant Seven－linkmanipulator Used in a Cucumber Picking Robot[J].Biosystems Engineering，2010，106：112-124.