基于仿生结构锡抛光垫的抛光接触压力分析

王 军 邢雪岭 吕玉山 张辽远

沈阳理工大学,沈阳,110159

0 引言

化学机械抛光是电子基片、光学平面和陶瓷平面等零件超精密加工的最重要方法。该技术在IC和MEMS制造领域中有着关键作用。在抛光过程中,工件抛光表面的接触压力场是导致被加工工件表面平面度下降和表面完整性不一致的关键因素。为了解决上述问题,许多学者从弹性力学接触理论出发,对接触压力进行了仿真与计算,分析得出了接触压力场分布不均的原因,并采用了一系列方法来解决该问题[1-2]。尽管取得了一定的成效,但是仍然没有得到全面有效的解决方案。因此,本文基于Winkler地基理论及叶序理论[3-4]设计了一种锡仿生结构抛光垫。

1 抛光的原理及锡仿生结构抛光垫

1.1 化学机械抛光的原理及问题

图1为化学机械抛光装置原理图。在抛光过程中,晶片安装在料架上并被压向抛光垫的上表面,抛光垫在抛光台支撑下绕主轴旋转。抛光液喷洒在抛光垫表面,晶片表面材料经过抛光液的化学腐蚀和抛光垫的机械摩擦被逐渐去除,从而达到除去晶片被抛表面材料的目的。

图1 化学机械抛光装置原理

在一般的化学机械抛光中,抛光垫材料的横向牵连效应使得接触表面压力分布不均匀,抛光液难以均匀地分布于接触区域内,抛光形成的废物也难以顺畅地排出。同时,抛光产生的摩擦热在向外传导过程中的不顺畅会导致温度场分布的不均匀。这些因素通常会导致工件表面材料去除的不均匀,因而会导致加工表面的宏观与微观几何形状精度下降。

1.2 锡仿生结构抛光垫设计

图2a是葵花籽粒分布的结构示意图[5],籽粒分布满足叶序理论中的Vogel方程[6]:

式中,r为籽粒极坐标半径;n为籽粒序数;k为叶序参数,是由生长率决定的;φ为叶序角。

这种叶序分布结构在大自然普遍存在,具有籽粒自分离和对热辐射的最大吸收效应,形成的叶列线沟槽对流体具有均布发散功能。

图2b所示为所设计的锡仿生结构抛光垫,其中,抛光垫直径为275mm,磨料半球直径 d=2.0mm。磨料半球材料为锡合金(Sn63/Pb37)。基垫材料为紫铜,厚度h=0.25mm。

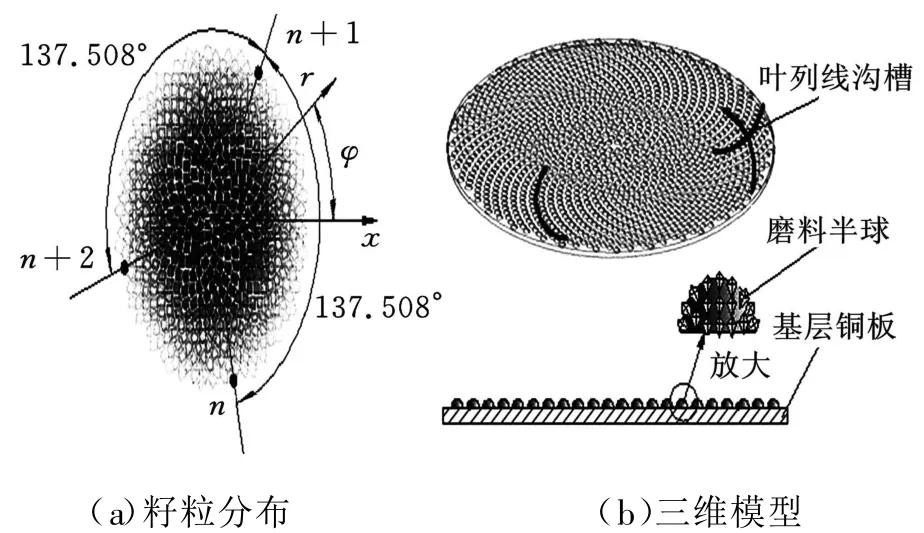
图2 籽粒分布及抛光垫三维模型

1.3 抛光的接触力学模型的建立

Winkler地基理论[7]把一个整体分割成无数个独立而没有横向牵连效应或剪切效应的单元个体。笔者设计的抛光垫磨料半球分布符合Winkler地基理论的这一要求。根据Winkler地基理论,Winkler地基的反力大小只与地基反应模量K及支撑物变形位移成正比,而在横向上没有牵连效应,所以晶片只受垂直方向上力的作用。抛光垫籽粒半球与晶片接触为非Hertz问题,且这种接触很难用解析法表达。有限元法是获得接触压力分布可行的方法之一。根据上述理论,建立图3所示的锡仿生结构抛光垫抛光的接触力学模型。

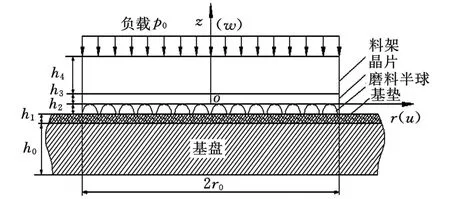
图3 锡仿生抛光垫接触力学模型

模型中,ur i、wzi分别为径向和轴向的变形位移,σri、σzi和τrzi分别为径向应力、轴向应力和剪切应力,A为晶片与料架接触区域,C和D分别为磨料半球与晶片、磨料半球与基垫间的接触区域,下标 0、1、2、3、4 分别表示抛光基盘 、基垫、磨料半球、晶片、料架。该问题的边界条件如下:

当z=h3+h4,即在料架上表面时

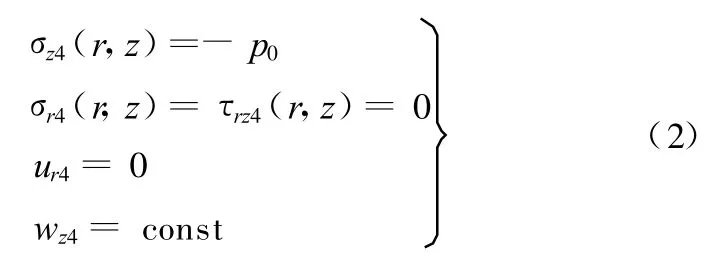
当z=h3,即料架与晶片接触时,若r∈A,则

若r ∉ A,则

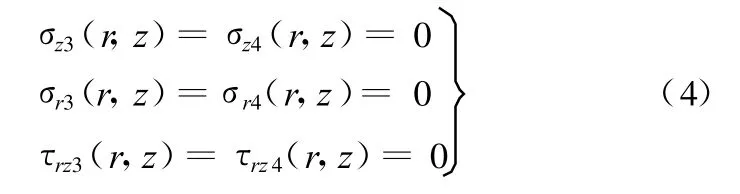
当z=0时,若r∈ A ∩ C,则

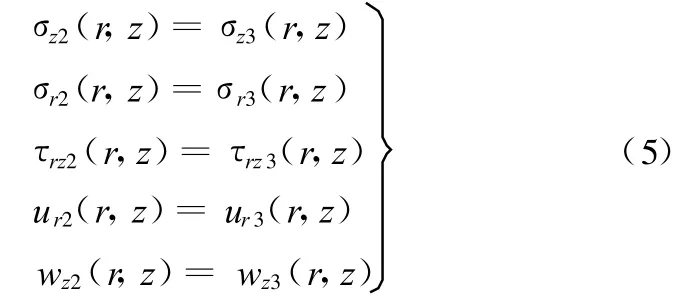
若r∉A∩C,则

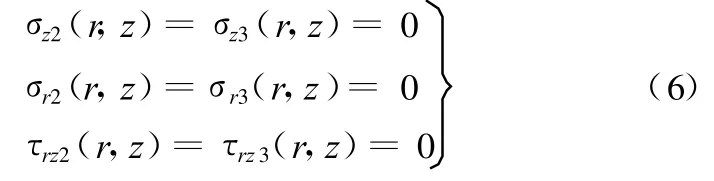
当z=-h2,即磨料半球与基垫接触时,若r∈A∩D,则

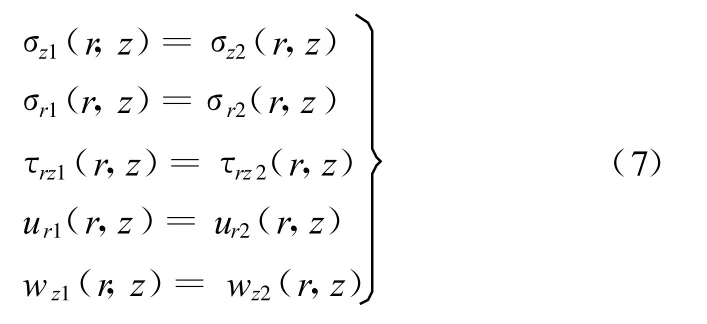
若r∉A∩D,则

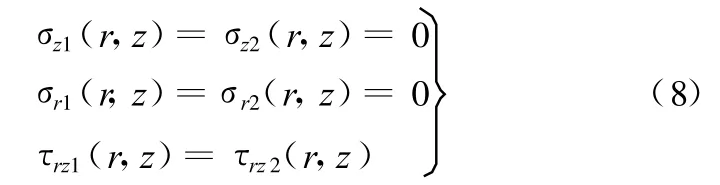
当z=-h1-h2,即基垫与基盘接触时,

晶片表面接触压力表达式为

2 仿真计算结果与分析

2.1 有限元计算的基本问题与已知条件

利用仿真软件ANSYS11.0建立有限元分析模型及边界条件[8-10],采用Solid45及Solid92单元对模型进行网格划分。对于要研究的区域进行网格细化,对其余部分网格粗糙划分,以减小电脑CPU资源占用率,提高计算速度。图4所示为有限元计算网格划分模型。

图4 有限元计算网格划分模型

本文主要研究抛光垫磨料半球的直径d及叶序参数k的变化对晶片表面接触压力分布的影响。已知条件为如下:抛光垫磨料半球直径d=2.0mm,基垫直径为275mm,厚度 h1=0.25mm,弹性模量 E1=120GPa,泊松比 ν1=0.326。工件为光学晶片,直径为 76mm,厚度h3=3mm,弹性模量E3=1.9GPa,泊松比ν3=0.278。基盘与料架为钢盘,其弹性模量E0=E4=215GPa,泊松比 ν0=ν4=0.28。料架顶部施加的压力p0=0.1MPa,基盘底部全约束。利用上述边界条件来计算晶片与抛光垫的接触界面压力。

2.2 接触压力的计算结果与分析

图5为普通锡抛光垫抛光的接触压力的二维应力及三维直观分布图。从图5可以看出,接触压力场的基本分布形态为压力从晶片中心到边沿逐渐增大,晶片在被抛光过程中,边缘处的抛光量大于中心部分的抛光量,从而导致晶片产生平面度误差和塌边现象。

图5 普通锡抛光垫对晶片表面接触压力分布的影响

图6所示为锡仿生结构抛光垫叶序参数k的变化对抛光接触压力分布的影响。图6中,随着叶序参数k值的增大,接触压力分布的均匀性越来越明显,边界效应也得到了明显的改善,相比普通锡抛光垫晶片,表面接触压力分布均匀性有了很大的提高。但是当叶序参数k增大到一定值后如果继续增加,晶片内部开始出现压力过大现象,这会导致晶片出现平面度误差。当叶序参数k=2.2时,晶片表面接触压力分布较为均匀。

图7为在不同的磨料半球直径d时晶片表面接触压力分布三维直观图。从图7我们可以看出,随着锡仿生结构抛光垫磨料半球直径d的增大,磨料半球与晶片接触有效面积也随之增大,晶片内外接触压力分布差值逐渐减小,磨料半球直径d超过2.0mm时,接触压力在晶片表面的分布开始变得不均匀。所以,接触压力在晶片表面分布呈现一种从不均匀到均匀再到不均匀的状态,当锡仿生结构抛光垫磨料半球直径d=2.0mm时,晶片表面接触压力的分布最均匀。此时晶片内外压力差值很小,晶片周边压力和内部压力趋于相等,晶片边缘材料单位去除量也变得较为合理,塌边现象变得不明显。

相对普通锡抛光垫抛光来说,利用锡仿生结构抛光垫抛光后的晶片表面接触压力场分布的均匀性有了较大的改善。普通锡抛光垫对于晶片的影响主要体现在晶片的边缘处,根据Preston方程,材料去除厚度正比于抛光接触压力,由抛光接触压力分布不均而导致的平面度误差也会随之增大。而锡仿生结构抛光垫能够很好地均匀晶片表面接触压力分布,如图6、图7所示。这些压力分布形态改变了整个晶片材料的去除量,晶片周边和内部接触压力分布均匀,晶片表面内外材料单位去除量基本相等。因此能够减小平面度误差并改善塌边现象。

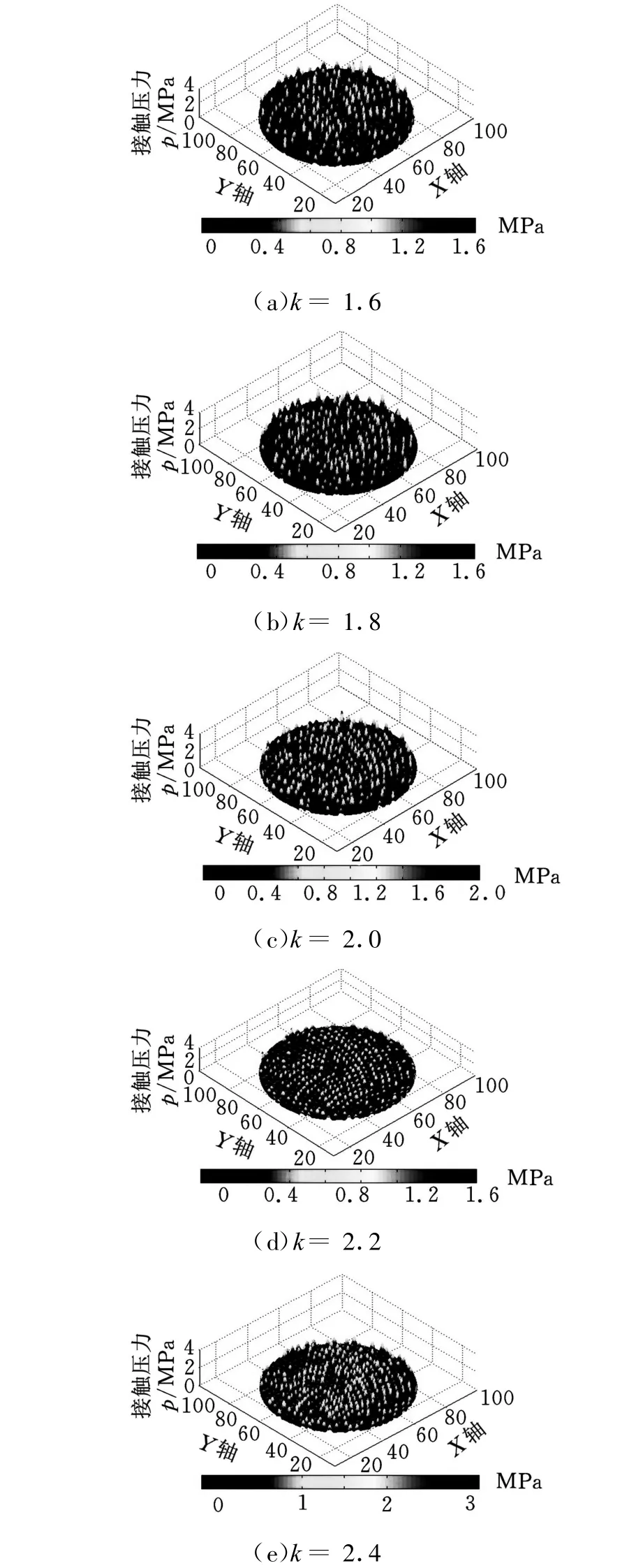
图6 不同的抛光垫叶序参数k对晶片接触压力分布的影响(d=2.0mm,p0=0.1MPa)

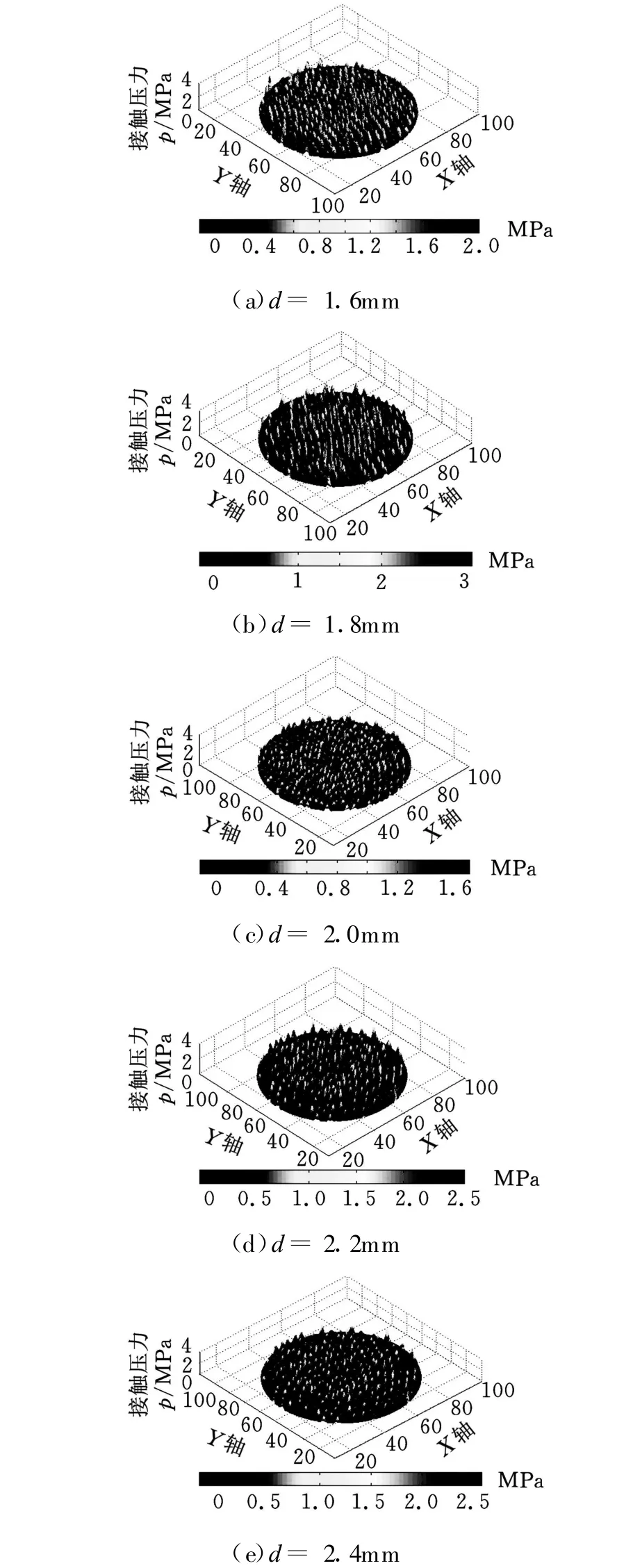
图7 不同的磨料块直径d对晶片接触压力分布的影响(k=2.2,p0=0.1MPa)

3 实验结果与分析

本实验是在摆式抛光机上进行的,抛光盘转速n=90r/min,抛光压力 p0=0.1MPa,摆臂摆幅α=25°,摆臂摆角 θ=15°,抛光液流量为60mL/min,实验温度为25～30℃,抛光时间t=90min。抛光液为PC-N100-W 型、体积分数为0.5%纳米金刚石抛光液。使用锡仿生结构抛光垫与普通锡抛光垫进行对比实验,实验完成后采用光学平晶在钠光灯下获得干涉条纹,经过计算机处理的结果如图8、图9所示。

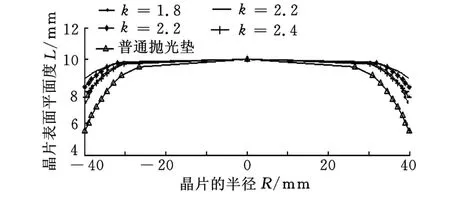
图8 叶序参数k对晶片表面平面精度的影响(d=2.0mm,p0=0.1MPa,t=90min)

图9 磨料半球直径d对晶片表面平面精度的影响(k=2.2,p0=0.1MPa,t=90min)

从图8可以看出,随着叶序参数k的逐渐增大,晶片抛光后的平面精度越来越不理想,晶片边缘产生的塌边现象越来越明显。叶序参数k越大,锡仿生结构抛光垫表面磨料半球分布密度就会越小,磨料半球与晶片接触的有效面积也越来越小,而当利用普通锡盘抛光垫抛光时,我们从图8可以看出,晶片的塌边现象很明显。采用仿生结构抛光垫抛光,当叶序参数k=2.2左右时,晶片的平面精度最为理想,塌边现象最不明显。

相比抛光垫叶序参数k的影响,抛光垫磨料半球直径d的改变也会对晶片平面精度产生影响。在实际情况中我们可以认为,磨料半球顶部很小的面积与晶片接触,由于叶序参数k的大小影响磨料半球的分布,改变磨料块直径大小,对磨料块与晶片接触有效面积影响很小。因此,磨料半球直径对晶片平面精度的影响远远不如抛光垫叶序参数k影响大。但是我们也可以从图9看出,随着磨料半球直径的增大,晶片表面精度越来越高,塌边现象也会越来越不明显,不过这种情况不如改变叶序参数k值时明显。当磨料半球直径d=2.0mm左右时,晶片表面平面精度最为理想。

4 结论

①锡仿生结构抛光垫减小了材料本身的横向牵连效应,使抛光压力得到了均匀化,解决了晶片边界压力增大的问题。②叶序参数k和磨料半球直径d是影响晶片表面接触压力均匀分布的主要因素。③当叶序参数k=2.2、磨料半球直径d=2.0mm时,晶片表面接触压力分布较为均匀。此时,能够使抛光的边界效应减小,晶片的塌边现象得到很好的改善。

[1]Lin Y Y,Lo S P.A Study on the Stress and Nonuniformity of the Wafer Surface for Chemical-mechanical Polishing Process[J].The International Journal of Advanced Manufacturing Technology,2003,22(5/6):401-409.

[2]Luo J F,Dornfeld D A.Material Removal Mechanism in Chemical M echanical Polishing:Theory and Modeling[J].IEEE T ransactions on Semiconductor Manufacturing,2001,14(2):112-133.

[3]Jean R V.Mathematical Approach to Pattern and Form in Plant Growth[M].New York:John Wiley&Sons Inc.,1984.

[4]Neumann P,Carpendale S,Agarawala A.PhylloT-rees:Phyllotactic Patterns for Tree Layout[C]//EUROVIS-Eurographics/IEEE VGTC Symposium on Visualization.Toronto,2006:59-66.

[5]Levitov L S.Phyllotaxis of Flux Lattices in Layered Superconductors[J].Phys.Rev.Lett.,1991,66(2):224-227.

[6]Vogel H.A Better Way to Construct the Sunflower Head[J].Mathematical Biosciences,1979,44(3/4):179-189.

[7]Chan S K,Tuba I S.A Finite Element Method for Contact Problems of Solid Bodies-Part I:Theory and Validation[J].Int.J.Mech.Sci.,1971,13(6):615-625.

[8]Wang D,Lee J,Holland K,et al.Von Miss Stress in Chemical Mechanical Polishing Process[J].Journal of Electrochemical Society,1997,144(3):1121-1127.

[9]Byme G,Mullany B,Young P.The Effect of Pad Wear on the CMP of Silicon Wafer[J].Annals of the CIRP,1999,48(1):143-146.

[10]Brebbia C A,Telles J C F,Weobel L C.边界单元法的理论和工程应用[M].龙述尧,刘腾喜,蔡松柏,译.北京:国防工业出版社,1998.