失效模式相关的机械结构可靠性的Copula分析方法

韩文钦 周金宇 孙奎洲

江苏技术师范学院，常州，213001

0 引言

在实际工程中，机械结构系统存在多种失效模式，各失效模式的功能函数有相同的随机载荷和几何参数，而且这些载荷、尺寸和材料性能参数具有不确定性，导致机械结构各失效模式间具有相关性[1－2]。对于具有多个失效模式或多个损伤机制的同一构件，如果在系统可靠性分析中忽略失效相关性，常常会导致较大误差。因此，定量分析失效相关性，基于失效相关的内在机制进行系统概率分析，对具有相关失效模式的结构系统进行可靠性理论研究尤为重要。

Ditlevsen[3]于1979年导出了结构系统失效概率的窄界限范围公式，当系统失效模式数n较大时，该方法计算繁琐，文献[4]应用Ditlevsen窄界限范围公式计算了结构系统的可靠度。Monte Carlo法在结构系统可靠度计算中被认为是一种准精确的计算方法[5]。方向重要抽样模拟法和β－球面外的截尾正态重要抽样模拟法可以获得系统失效概率的精确解[6]，从而可以验证其他计算系统失效概率方法的精度，这两种模拟法每一次抽样后都需要进行有限元分析才能够获得极限状态函数值，其计算量很大。文献[7-8]提出的计算结构系统可靠度方法通过线性相关系数ρ把系统分为几个阶段，隶属于某个阶段的系统可靠度取平均值，其结果为近似解。

作为统计分析的新工具，Copula能以简洁、灵活的函数形式实现多元随机变量的概率建模，可以由多种边际分布函数来推求联合分布函数，构造随机变量间的相关结构，刻画随机变量之间统计相关的非线性特征。Copula在金融保险、水文分析等领域的相关分析的应用上得到迅速发展[9－12]。本文针对具有相关失效模式的机械结构系统，初步利用混合Copula函数对机械零部件结构系统进行可靠性建模和分析，为具有相关失效模式的机械机械结构系统可靠性分析提供新思路。

1 Copula函数简介

Copula理论基于 Sklar定理[13]：功能函数，令 H 为k维联合分布函数，其边缘分布函数分别为F1，F2，…，Fk，则存在唯一的k－Copula函数C使得对于

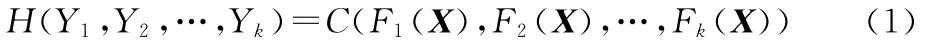
可见，Copula可把多维随机变量Yj的联合分布函数H（·）显式表达为所有一维边缘分布函数Fk（X）的连接函数C，Copula函数能独立于随机变量的边缘分布反映随机变量的相关性结构，通过分别独立分析变量间的相关性结构和变量的边缘分布来研究其联合分布，其中相关性结构用Copula函数来描述。Copula函数的优点在于任意边缘分布经过Copula函数连接都可构造成联合分布，而且还可以刻画随机变量之间的复杂非线性相关结构。

Copula函数的种类很多，下面主要介绍Archimedean族的Copula函数。Gumbel Copula函数为

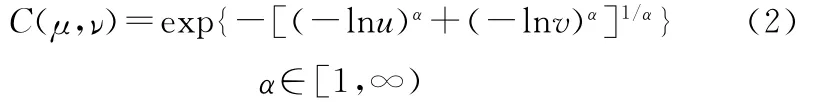
Clayton Copula函数为

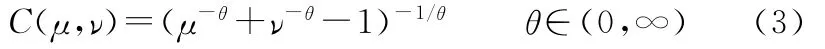
以上两种Copula函数，当参数α→1，θ→0时，随机变量μ、ν趋于独立；当α→∞、θ→∞时，随机变量μ、ν趋向于完全相关；两种Copula函数的概率密度见图1。

Gumbel Copula函数对变量在分布上尾处的变化十分敏感，可用于描述具有上尾相关特性的变量之间的相关关系，若随机变量间的相关结构可以由Gumbel Copula函数来描述，就意味着在分布的上尾变量间具有更高的相关性，对上尾拟合较好 ，但对下尾拟合较差。Clayton Copula函数对变量在分布下尾处的变化十分敏感，可用于描述具有下尾相关特性的变量之间的相关关系。

机械零部件各失效模式间具有非对称相关模式，很难用一个简单的Copula函数来全面刻画失效模式间的相关关系，因此有必要构造一种更为灵活的Copula函数以描述不同失效模式间的相关关系。本文选用由Gumbel和Clayton两个Copula函数的线性组合构造混合Copula函数，用这两种典型相关模式的组合反映失效模式间的相关变化情况。混合Copula函数的基本形式为

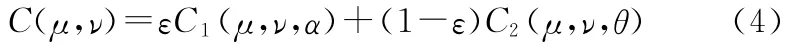
图1 二元Copula函数概率密度图

式中，C1、C2分别为 Gumbel和Clayton Copula函数；ε为加权系数，加权系数的大小反映了变量间相关模式。

因此，混合Copula函数可以描述具有不同相关模式的变量间的相关关系，相对于单一Copula函数更灵活、适用性更广泛。

2 机械结构系统的Copula可靠性模型

在实际工程中，一个结构系统有多种失效模式，研究结构系统的可靠性问题需要计算多个失效模式下的联合失效概率。

设某结构系统含有k个失效模式，对应于不同的失效模式，其功能函数可表示为

若用Ej表示第j个失效模式出现这一事件，则有

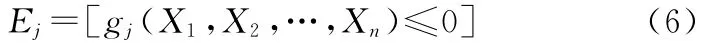
结构系统的失效概率可表示为

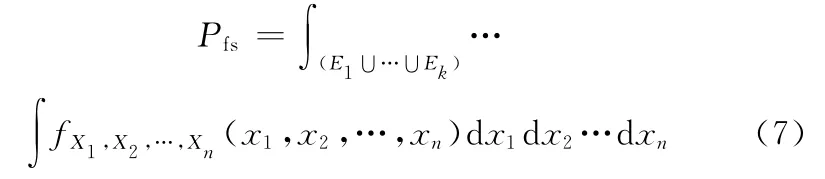
由式（7）可见，求解机械零部件系统的失效概率需要计算多重积分，各随机变量的联合概率密度也难以得到。近些年来，计算结构系统失效概率使用了很多近似计算方法[6]。

结构的系统失效可以分为三类：第一类是串联系统，它是指所有极限状态中任意一个发生失效，就认为结构失效；第二类是并联系统，它是指所有极限状态都失效，才认为结构系统失效；第三类称为串并联系统，它由串联系统和并联系统组合而成，实际中最常用到的串并联系统是认为结构的系统失效是由很多个失效模式组成的串联系统，而每个失效模式又是由多个失效模式组成的并联系统。

串联系统的失效概率为

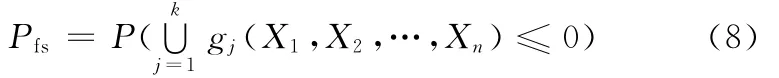
并联系统的失效概率为

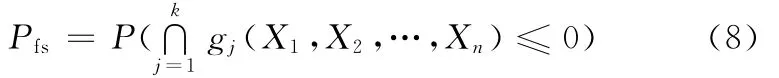
串并联系统的失效概率为

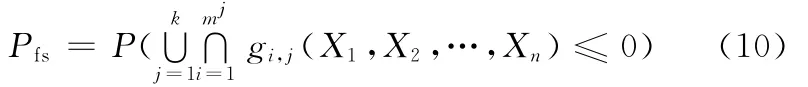
串联系统和并联系统之间可以进行转化：

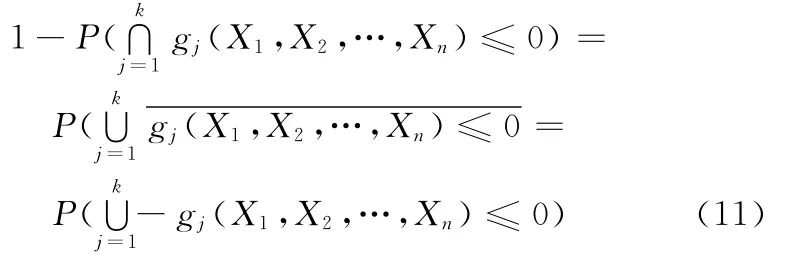
所以，串联系统和并联系统可以用相同的求解方法获得失效概率。而求解串并联系统的失效概率一般要将第i个并联系统失效模式等价为一个极限状态gj＝0，再将各失效模式组成串联系统，用串联系统求解失效概率的方法获得串并联系统的失效概率。于是，求解结构系统失效概率的核心问题就是如何求解多个失效事件的串联系统发生概率。

2.1 串联系统

当系统有两个失效模式时，其功能函数见式（5），此时j＝1，2，令Pfj为各失效模式的失效概率，C（·）表示Copula函数，则系统失效概率为

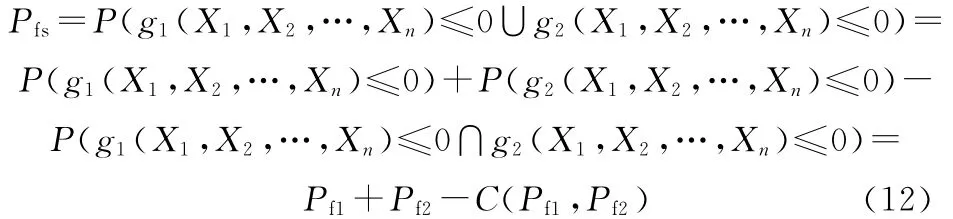
当系统有k个失效模式时，系统失效概率为

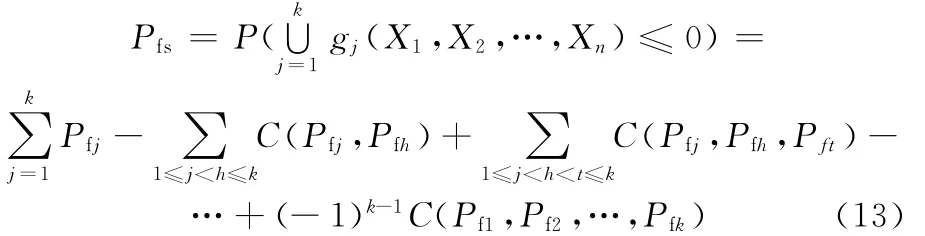
2.2 并联系统

当并联系统有k个失效模式时，系统失效概率为

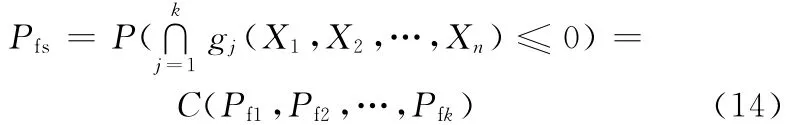
2.3 串并联系统

以图2中4个失效模式为例，其他有多个失效模式时与之类似。令两个并联系统的失效事件分别为E1＝[g1≤0∩g2≤0]，E2＝[g3≤0∩g4≤0]，对于第i个并联系统的分布函数存在Copula函数，记为Ci（i＝1，2），对于整个系统存在Copula函数，记为C，则系统的失效概率为

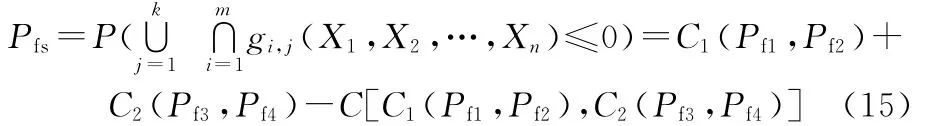
图2 串并联系统可靠性框图

3 机械系统可靠性的Copula分析方法

应用混合Copula方法分析结构系统可靠性，关键是混合Copula的建模，即参数估计和检验。本文利用Monte Carlo法产生的随机抽样数据估计和检验Copula参数，实现结构系统的可靠性建模和分析计算，具体计算步骤如下：

（1）Monte Carlo抽样。利用Monte Carlo模拟法，对结构系统中每个失效模式的功能函数中所有随机变量按照其分布进行抽样，把抽样的随机变量代入各功能函数，每个功能函数产生与抽样的随机变量相对应的随机序列值｛Gj｝i（i＝1，2，…，n），利用MATLAB软件将每个功能函数随机序列值转化为相应的经验分布函数序列值（Fj）i，其中（Fj）i＝F（｛Gj｝i）。

（2）Copula函数的参数估计。采用离差平方和最小准则（residual square sum，RSS）来选择Copula的参数，RSS计算公式为

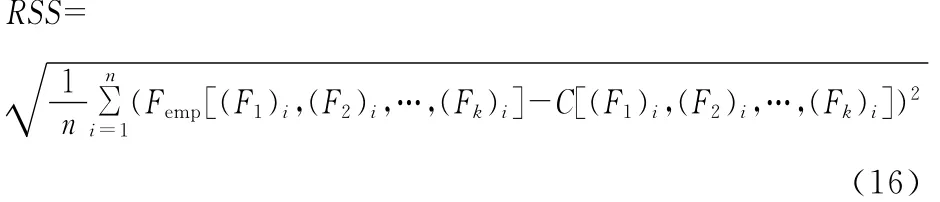
最优的参数估计值应使得RSS最小。然后利用MATLAB软件优化工具箱中的fmincon函数快速求解各待定参数。

（3）Copula函数拟合优度评价。利用随机抽样数据，将由Monte Carlo法得到的经验联合分布值F′emp与随机抽样数据相对应的由鞍点逼近和混合Copula函数得到的累积分布值绘制二维和三维散点关系图，如果二维散点图上的数据点都落在45°对角线附近，三维散点图上点基本接近或重合，表明Copula函数拟合得好。

（4）应用混合Copula函数分析结构系统的可靠性。

4 数值算例

图3为承受轴向载荷的两端简支空心压杆的受力简图。基本变量 P、E、S、d、t、l分别表示轴向载荷、材料弹性模量、材料屈服极限、截面中径、壁厚和杆长，均服从正态分布，分布参数见表1。

图3 空心压杆

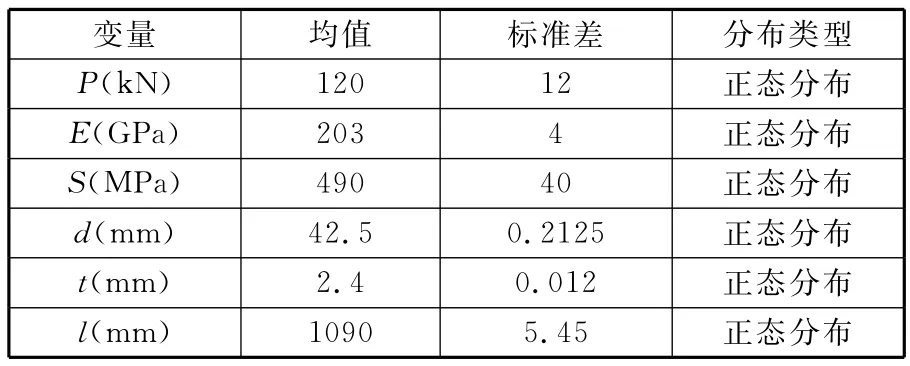
表1 基本变量的分布参数及类型

此压杆结构存在强度和稳定性两种失效模式，其功能函数分别为

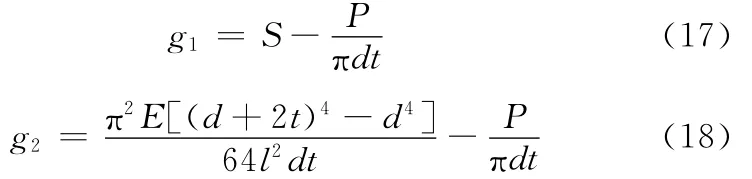
压杆结构为串联系统，两种失效模式的功能函数都含有相同的随机变量，其失效模式之间存在相关性。根据计算步骤（1）可以得到g1和g2的经验分布函数序列值（Fj）i，绘制两个功能函数的联合经验分布函数散点图（图4），从图4可得知g1与g2在上尾和下尾处具有很强的相关性。

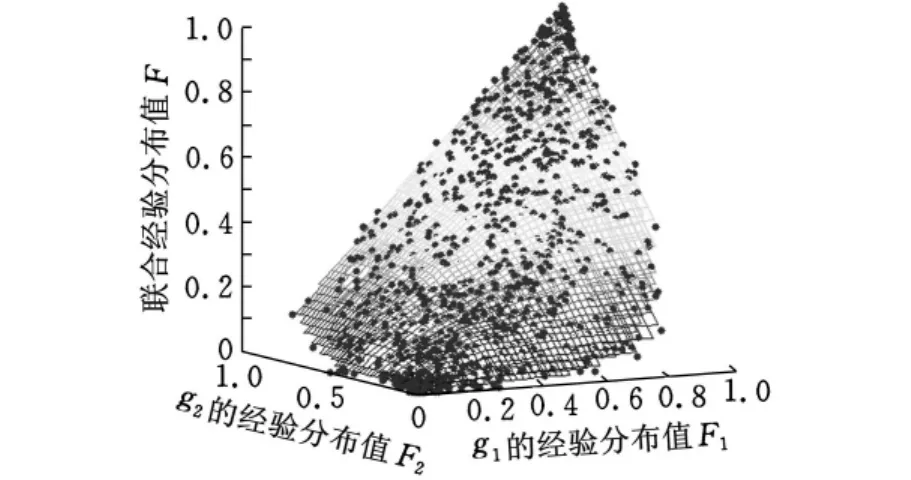
图4 联合经验分布函数散点

采用离差平方和最小准则法确定混合Copula待定参数ε＝0.5675，α＝2.6480，θ＝2.8890。由图5和图6可知，此混合Copula函数拟合两个失效模式的联合分布函数较好。

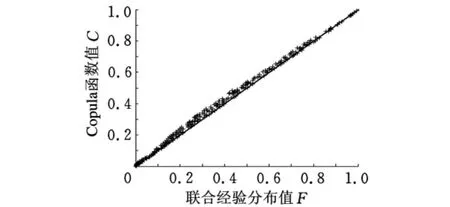
图5 经验联合分布值与Copula函数值散点图

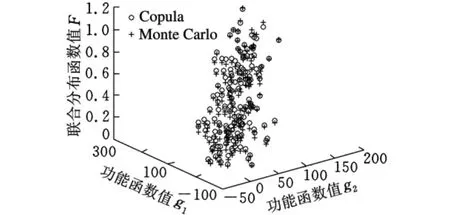
图6 联合分布值散点图

两个失效模式的失效概率可以应用已有的方法进行计算[6]，本文采用 Monte Carlo计算得到g1和g2的失效概率分别为Pf1＝0.0178，Pf2＝0.0281，利用式（4）和式（12）可计算得结构系统的失效概率Pf＝0.0428。应用Monte Carlo模拟法，抽样次数为n＝106次可得结构系统的失效概率Pf＝0.0396。从可靠性分析结果可以看出，基于Copula函数方法计算结果与Monte Carlo法大样本模拟所得估计值吻合较好。

5 结语

混合Copula函数是综合了几种Copula函数的优点而构造的一种多参数的Copula函数，改善了单一参数Copula灵活度不高的缺陷，可以刻画变量间的非对称结构和尾部相关性，构建变量间的相关数值模型。

本文在具有相关失效模式的结构系统可靠性计算中初步应用混合Copula方法，以各失效模式的功能函数作为随机变量，通过各失效模式的经验边缘分布，应用Monte Carlo抽样估计Copula函数的参数，建立结构系统的Copula可靠性计算模型，进而对结构系统进行可靠性分析。研究结果为解决失效模式相关的结构系统的可靠性分析提供了一种新途径。

[1]周金宇，谢里阳，韩文钦，等.基于 Nataf变换的载荷相关系统风险预测方法[J].机械工程学报，2009，45（8）：137-141.

[2]张义民，张旭方，杨周，等.多失效模式机械零部件可靠性灵敏度设计[J].机械强度，2009，31（6）：926－931.

[3]Ditlevsen O.Narrow Reliability Bounds for Structural System[J].Mechanics Based Design of Structures and Machines，1979，7（4）：453－472.

[4]吴帅兵，李典庆 ，唐小松.水工钢闸门主梁失效模式间相关性分析[J].武汉大学学报（工学版），2009，43（3）：217-321.

[5]王岩，尹海丽.蒙特卡罗方法应用研究[J].青岛理工大学学报，2006，27（2）：111－113.

[6]秦权，林道锦，梅刚.结构可靠度随机有限元[M].北京：清华大学出版社，2006.

[7]喻天翔，宋笔锋，万方义，等.机械零件多失效模式相关可靠度算法研究[J].机械强度，2006，28（4）：508－511.

[8]周金宇，谢里阳，王学敏.失效相关结构系统可靠性分析及近似求解[J].东北大学学报，2004，25（1）：74－77.

[9]韦艳华，张世英.多元Copula－Garch模型及其在金融风险分析上的应用[J].数理统计与管理，2007，26（3）：432－439.

[10]Yang Jingping，Cheng Shihong，Zhang Lihong.Bivariate Copula Decomposition in Terms of Comonotonicity，Countermonotonicity and Independence[J].Insurance：Mathematics and Economics，2006，39：267－284.

[11]郭生练，阎宝伟，肖义，等.Copula联结函数在多变量水文分析计算中的应用及研究进展[J].水文，2008，28（3）：1－7.

[12]De Michele C，Salvadori G，Passoni G，et al.A Multivariate Model of Sea Storms Using Copulas[J].Coastal Engineering，2007，54：734－751.

[13]Nelsen R B.An Introduction to Copulas[M].New Yark：Springer，2006.