基于多软件平台协同工作的FIR滤波器设计*
2011-09-06陈立万王海峰
曾 伟,陈 强,陈立万,陈 卓,王海峰
(1.重庆三峡学院应用技术学院,重庆万州404100;2.重庆三峡学院电子与信息工程学院,重庆万州 404100)
0 引言
1992年美国Lattice公司发明了在系统可编程技术,彻底改变了传统数字电子技术系统的设计和实现方法,开创了数字系统设计的革命性时代。在1999年,Lattice公司又推出了在系统可编程模拟电路,为电子设计自动化技术的应用开拓了更为广阔的前景[1]。
随着信息科学和计算机技术的迅速发展,数字信号处理在20世纪末期得到了飞跃式的发展。在数字信号处理中数字滤波是重要的环节,经典数字滤波器从实现的网络结构或者单脉冲响应长度分类,主要分为有限脉冲响应(FIR)和无限脉冲响应(IIR)两大类;与IIR滤波器相比FIR滤波器的计算工作量稍大,但是在保证幅度特性满足技术要求的同时,很容易做到严格的线性相位特性[1]。
1 系统的总体结构设计
由于数字信号处理是用数值运算的方式实现对信号的处理,因此,相对于模拟信号处理,数字信号的处理具有灵活性、高精度和高稳定性、便于大规模集成、而且可以实现模拟系统无法实现的诸多功能。

图1 数字滤波器信号处理过程
图1所示为数字滤波器的信号处理过程。数字信号处理的对象诸如语音信号等它们本身也是模拟信号,所以一般先经过缓冲以及模拟信号预滤波,然后利用模-数转换器(A/D转换器)将模拟信号转换成数字信号,再利用FPGA构成的FIR数字滤波器处理转换后的信号。进一步利用数-模转换器(D/A转换器)将数字滤波器处理过的结果转换为模拟信号供使用。
2 系统各部分功能的设计与实现
2.1 前端缓冲、预滤波以及模数转换部分结构[1]
这部分的缓冲以及预滤波由ispPAC20来完成,然后利用FPGA以及ispPAC20中的D/A转换器、比较器共同构成逐次逼近式A/D转换器,其中ispPAC20中的电路结构图如图2所示。
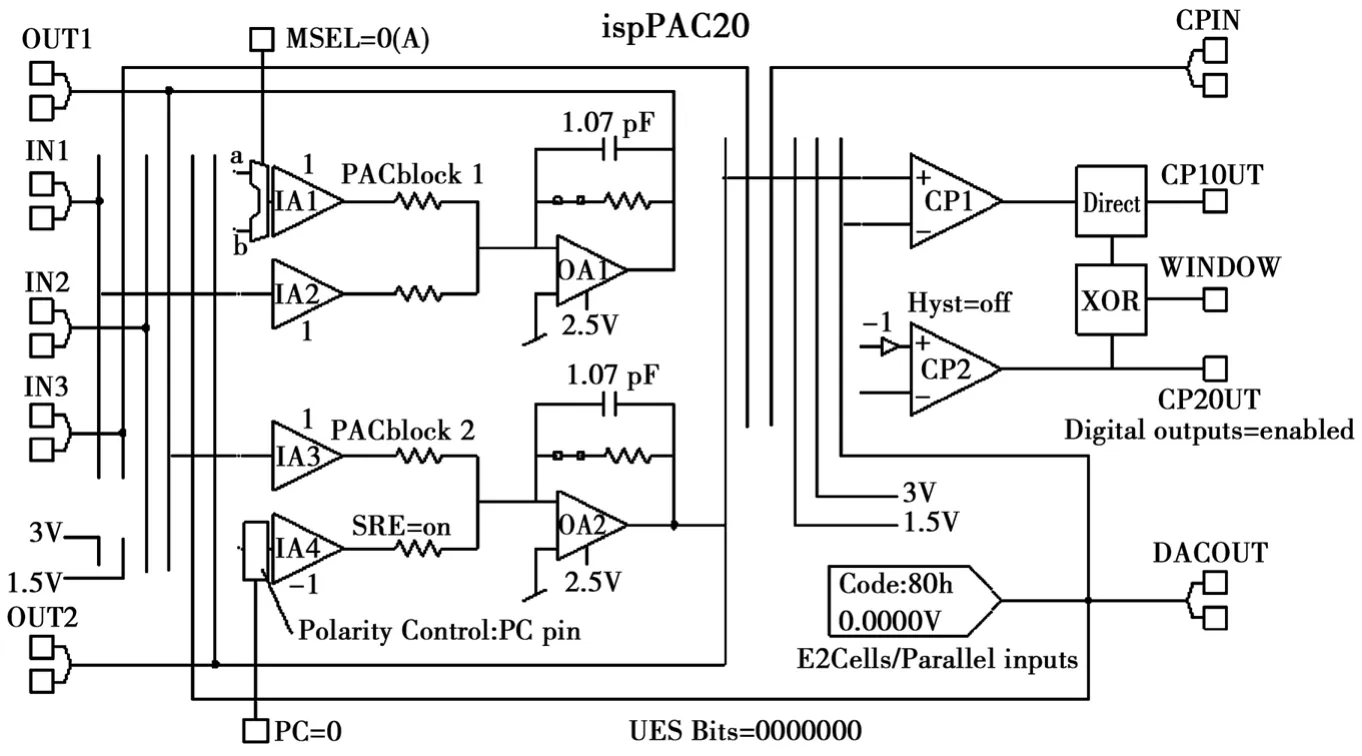
图2 前端ispPAC20内部连线图
逐次逼近式A/D转换器原理如图3所示,当启动信号START到来后,8位逐次逼近寄存器SAR(Successive Approximation Register)清零,转换过程开始。第一个时钟脉冲到来时,SAR最高位置1,其余位为0。SAR中锁存的数据为10 000 000,经过DAC转换后得到的输出电压Vda,与输入电压Vi进行比较,若Vi大于Vda,则SAR最高位的1被保留,否则清零。

图3 逐次逼近式A/D转换器原理
第二个脉冲到来时,SAR次高位置1,所得的新值经过DAC转换后得到的电压Vda再与Vi进行比较,若Vda小于Vi则SAR次高位1被保留,否则清零。重复上述过程,依次类推,从D7~D0都比较完毕,转换便结束,结束后SAR的数据输出到输出寄存器作为输出数字量。从而经过ispPAC20和FPGA共同完成从模拟量到数字量的转换[2]。
2.2 数字滤波部分
2.2.1 FIR数字滤波器的设计原理分析[3]
FIR数字滤波器的构成形式主要有直接型、级联型、线性相位型FIR滤波器和频率采样型等。本文采用直接型结构,故N阶FIR数字滤波器的传递函数为:
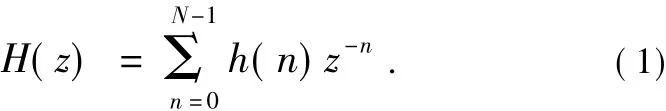
H(z)是z-1的N-1次多项式,它在z平面上有个N-1零点,在原点z=0处有一个N-1重极点,因此系统函数H(z)永远稳定。系统差分方程表达式为:


其中M为FIR滤波器的抽头数;h(k)为第k级抽头系数(单位冲击响应);x(n-k)为延时k个抽头的输入信号。
2.2.2 滤波器系数的计算[4]
数字滤波器实际上是一个采用有限精度算法实现的线性非时变系统,它的步骤为先根据需要确定滤波器的性能指标,然后利用Matlab提供的滤波器设计工具——FDAtool仿真设计滤波器进行系数的设计。本系统的设计指标:设计一个8阶低通滤波器,模拟信号的采样频率为50 kHz,信号的截止频率为2 000 Hz,输入序列带宽为8位。因为在FIR数字滤波器之后的ispPAC20中的D/A转换器为8位,所以在设置滤波器系数的时候要限制输出位数。
FDATool计算出的值是一个有符号小数,而在 DSP Builder下建立的FIR滤波器模型需要一个整数作为滤波器系数。所以必须进行量化,并对得到的系数进行归一化处理。
2.2.3 FIR数字滤波器模型的搭建[4]
DSP Builder是一个系统级(或算法级)设计工具,它构架在多个软件工具之上,并把系统级和RTL级两个设计领域的设计工具连接起来,最大程度地发挥了两种工具的优势。
根据FIR数字滤波器的原理,在Matlab/simulink中进行设计的输入,利用Altera DSP Builder中的模块进行滤波器模型的搭建,然后将计算好的FIR数字滤波器系数输入到搭建的模型中,图4所示为搭建好的FIR数字滤波器模型。
上式就是输入序列x(n)与单位冲击响应h(n)的线性卷积,由上式可知n时刻的输入y(n)仅于n时刻的输入以及过去N-1个输入值有关,实际上FIR数字滤波器是由一个“抽头延迟线”加法器和乘法器的集合构成的。赋给每个乘法器的操作数就是一个FIR系数。
线性相位型FIR数字滤波器相位响应是频率的线性函数,即:

其中β=0或π/2,α是常数。
该因果系统具有严格的线性相位,当M为偶数时,有:

图4 FIR数字滤波器模型
在搭建好的模型中加入两个正弦波合成的输入信号,运行仿真,通过Scope窗口观察滤波器时域仿真波形如图5所示。
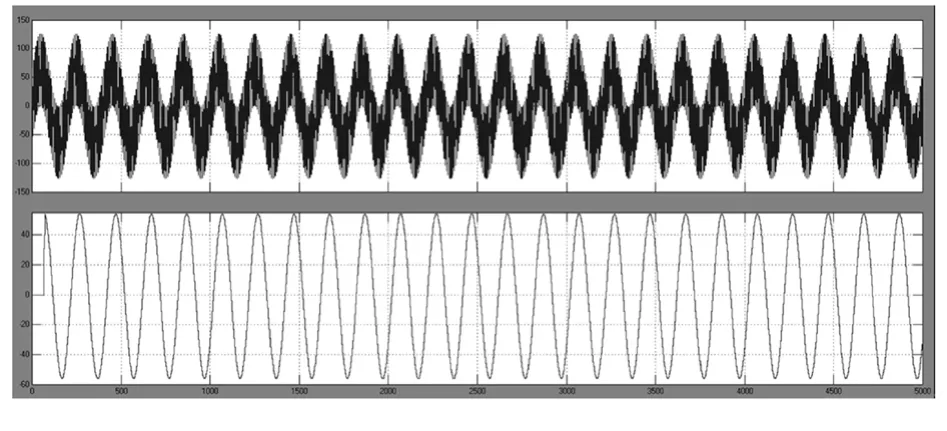
图5 滤波器时域仿真波形
从仿真的结果看,FIR滤波器输入信号上面叠加的带外信号得到有效滤除,效果为理想。
但是由于EDA工具软件(诸如QuartusⅡ和ModelSim)不能直接处理MATLab的.mdl文件,这就需要一个转换过程。通过 SignalCompiler把 Simulink的模型文件(后缀为.mdl)转化成通用的硬件描述语言——VHDL文件。转化后获得的HDL文件是基于RTL级的,即可综合的VHDL描述。然后对VHDL的RTL代码和仿真文件进行综合、编译适配及仿真。
2.3 后端模拟部分[5]
信号经过FIR数字滤波以后,生成的数字信号经过isp-PAC20内部D/A转换器,将数字信号转换成模拟信号,然后通过ispPAC20内部器件进行最后的模拟滤波,滤除信号中的叠加的某些高频分量,经过实际验证,得到的信号能够满足设计要求。
2.4 系统整体功能的实现
将原始信号经过ispPAC20的IN1口输入,经过内部程序的缓冲以及预滤波作用之后,将信号输入到比较器cp1的比较端口,然后与8位逐次逼近寄存器(SAR)输出的数字量经过内部D/A转换器输出的信号进行比较,从而完成从模拟信号到数字信号的转换过程。经过FPGA对转换后的数字信号的滤波处理之后,从FPGA的管脚输出,再通过后端ispPAC20的D/A转换器以及内部的运放以及输出滤波等程序,将信号从ispPAC20输出,从而完成系统的整个功能。
3 结束语
本系统改变了传统的只用硬件电路设计的方法,系统中前端模拟部分和后端模拟部分均采用可编程模拟器件(isp-PAC)实现,使用高度集成化芯片,系统的可靠性与稳定性有所提高,而且利用FPGA可以根据自己的要求重复配置各种精度和特性的FIR滤波器,使设计更为灵活,但由于利用isp-PAC20和FPGA构建的A/D转换器在转换精度和速率上有一定的限制,所以此系统在实际工程应用中还存在一定的局限性。
[1]陈立万,陈强,赵威威.EDA技术与实验[M].重庆三峡学院电子与信息工程学院自编教材,2011.
[2]张石,李景华,许桂芝,等.用ispPAC20和isp1032实现可编程逐次逼近式A/D转换器的研究[J],电子电气教学学报,2001,23(2):36-39.
[3]Uwe Meyer-Baese.Digital Signal Processing with Field Programmable Gate Arrays(Second Edition)[M].Spinger Press,2004.
[4]潘松,黄继业.EDA技术与VHDL[M].北京:清华大学出版社2005.
[5]赵曙光,殷延瑞,赵明英,等.可编程模拟器件原理开发及应用[M].西安:西安电子科技大学,2002.
[6]Steve Kilts.Advanced FPGA Design:Architecture,Implementation,and Optimization[M].JOHN WILEY & SONS,2007.
