静水中单个气泡的动力学特性数值模拟
2011-09-05徐玲君邵建斌
徐玲君,陈 刚,邵建斌,薛 阳
静水中单个气泡的动力学特性数值模拟
徐玲君1,陈 刚1,邵建斌1,薛 阳2
(1.西安理工大学水利水电学院,西安 710048;2.四川大学水力学与山区河流开发保护国家重点实验室,成都 620020)
为研究水中气泡上升的动力学特性,采用数值模拟方法,以静止水中的单气泡为研究对象,应用CFD分析软件,建立了气泡在浮力和重力作用下的仿真模型。模拟区域考虑了静水压力梯度场,采用无滑移技术处理流场边界及全结构网格技术处理气泡,对直径为2.6 mm和4 mm的气泡进行了数值模拟。分析了气泡在水中的运动机理,并将数值计算与实验数据进行了对比。结果表明:气泡在水中的上升路径与上升速度与试验结果吻合良好,此方法为利用数值手段研究水中气泡的运动特性提供了一个有效的解决途径。
气泡;数值模拟;运动机理
1 概 述
气泡运动广泛存在于许多工程实际中,从20世纪60年代开始,许多学者已经开始了关于气泡在液体中运动的试验与理论研究,几乎所有的研究内容都是2种互不溶解的流体,且大部分为气体进入液体,在没有热交换的条件下气泡在水中的运动过程。关于这一问题的较好总结,有Clift等[1]和Tsuge[2]。Tomiyama[3],Okaw[4]等一些学者已经先后对气泡的变形进行了研究,并引入了无量纲参数Re数、Eotvos数、Morton数来完成这一任务。

式中:g为重力加速度;ρf和ρb分别为液体和气体的密度;μf和μb分别为液体和气体的粘性系数;σ是表面张力系数;d是气泡直径;U为气泡的运动速度。
理论分析仅限于简单的规则情形,而试验研究的可重复性和可变性较差。气泡的结构是相当复杂的,同时又有一定的典型性,这种结构在其周围流体的影响下,会引起几何结构和拓扑结构方面的变化,因此,到现在为止,一种比较全面地能够捕获动态气泡的全部效应模型仍然是不存在的。本文采用CFD软件对水中气泡的上升过程进行了三维数值模拟,通过引入连续表面张力模型,得到了气泡的形状变化等数据,得到了气泡在没有热交换情况下的速度和形状随时间和上升高度变化的数据,并且将模拟结果和实验数据进行了对比。
2 数值模拟方法
在本文模拟的多相流系统中,由于模型计算区域内存在有不可压缩的水气两相流体,二者之间存在交界面。假设两液体相互不混掺,均为牛顿流体,在计算过程中没有传热等化学反应发生,则该水、气两相流系统可以用下面的不可压缩流体的连续方程与动量方程来描述:
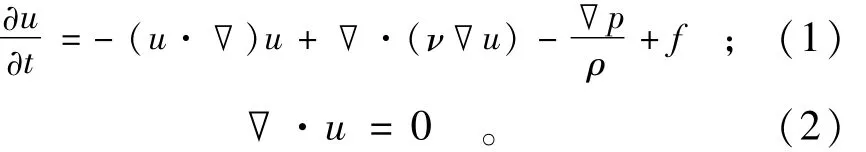
式中:u为速度;p为压力;ν为粘性系数;ρ为密度;f为外部因素,外部因素包括重力,浮力,表面张力和其它自定义的因素。
除了对速度场和压力场进行离散之外,气液接触面也需要进行描述和推理。本文采用VOF方法来追踪水气交界面。VOF法是Hirt&Nichols于1981年提出的[5],模型通过求解单独的动量方程和处理穿过区域的每一流体的容积比来模拟2种或3种不能混合的流体。相函数是VOF方法中的一个重要基本概念,它表示某一相介质占据网格面积或体积的百分数,相函数F取0到1之间的数值。VOF方法在确定自由水面具体位置时采用几何结构重建格式,即采用分段线性近似的方法来表示自由水面,它假定两流体之间的界面在每个单元内有个线性斜面,并使用这个线性形状为穿过单元面的流体的水平对流做计算。因此可以认为VOF方法是目前模拟自由表面水流问题较为理想的方法。
对于气泡的表面张力,和大尺度现象不同,气泡主要是由表面张力控制的,因此表面张力效应成为气泡运动真实性的一个关键因素,因此,本文采用了CSF(continuum surface force连续表面张力)模型来引入气泡所受到的表面张力。
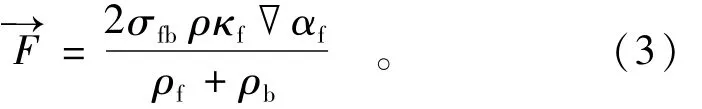
式中:σfb为表面张力系数;κf为表面曲率;▽αf为水相体积分数的梯度。
当气泡与固体壁面相接触时,它的运动会受到墙体壁面粘附的影响,因此,模拟中将壁面设置为无滑移边界条件,并且距离气泡运动范围足够远,保证壁面对气泡运动不产生影响。
3 模拟结果与讨论
本文模拟了三维气泡在静止水中重力和浮力作用下上升和变形的过程。众所周知,浮力和阻力控制着液体中气泡上升的速度,浮力和阻力受到液体性质、重力及气泡当量直径的影响很大。模拟区域为长方柱体,根据计算气泡的直径不同采用的计算区域不同,长宽高分布为3~12 cm。气泡初始速度为零,置于计算区域底部正中,在浮力作用下开始上升。采用六面体结构网格划分区域,划分的体积单元数分别从60万~80万不等。
液体与气体具有不同的性质,假定液体没有蒸发,气体没有在水中溶解,那么气泡的质量是恒定的,并且忽略了温度和压力沿程变化,这样就保证了气泡的体积也不发生变化。在模拟中气泡在上升过程中初始计算时刻保持球形形状,如图1所示。
图2给出了直径为2.6 mm和4 mm气泡上升过程中的路径变化情况,由于二者计算区域即长宽高不同,因此最后得到的气泡分辨率也有不同。2.6 mm气泡采用3 cm×5 cm×5 cm的计算区域,4 mm气泡采用4 cm×12 cm×12 cm的计算区域。
气泡直径分别为2.6 mm和4 mm时,气泡Re数分别为4 13和79 0左右,Eo数分别为0.88和

图1 气泡初始形状Fig.1 The initial shape of bubble

图2 2.6 mm与4 mm气泡上升过程Fig.2 The rising processes of 2.6 mm bubble and 4 mm bubble
2.15 ,气泡从初始形状的球形开始发生变形,随着气泡位置的上升,球形逐渐转为为椭圆形,上升路径逐渐呈现摇摆的螺旋形运动。从图2中可以看出:气泡直径越小,变形幅度越小,大气泡在运动过程中出现了翻转等情况,说明气泡直径越大,气泡受力越不均匀,运动就越复杂。
气泡最终的变形形状如图3所示。从图3中可以看出,除了上升和变形之外,气泡在运动过程中存在翻转和滚动等运动状态,这些状态一般是在雷诺数较大的情况下出现,随着气泡变形的幅度增大,直接导致了气泡的表面曲率增大,因此气泡的尾涡变得不对称,也变得更加不稳定,这样,不稳定的尾涡就导致了气泡的上升路径变得不稳定,呈现出不规则路径如之字形、螺旋形的状态。
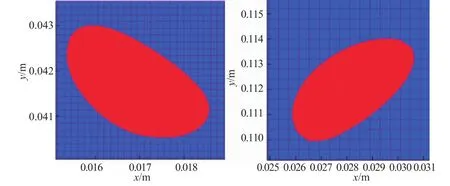
图3 2.6 mm与4 mm气泡最终变形形状Fig.3 The final shapes of 2.6 mm and 4mm bubble
图4 给出了气泡速度随着上升时间变化的关系,目前的模拟结果显示,经过最初的加速区域后,气泡并没有达到一个稳定的状态,而是达到一个周期性的振荡状态。由于浮力、重力及其他力的作用,气泡上升最终速度在某一值上下波动,随着气泡直径的增大,气泡尾部的涡旋增大,气泡受到的阻力增大,因此气泡的上升速度有所下降。图4就很明显地给出了这样一个过程:4 mm气泡的终速度小于2.6 mm气泡的终速度,但是4 mm气泡的振荡较2.6 mm气泡剧烈,是由于大气泡形状的振荡较大所致。
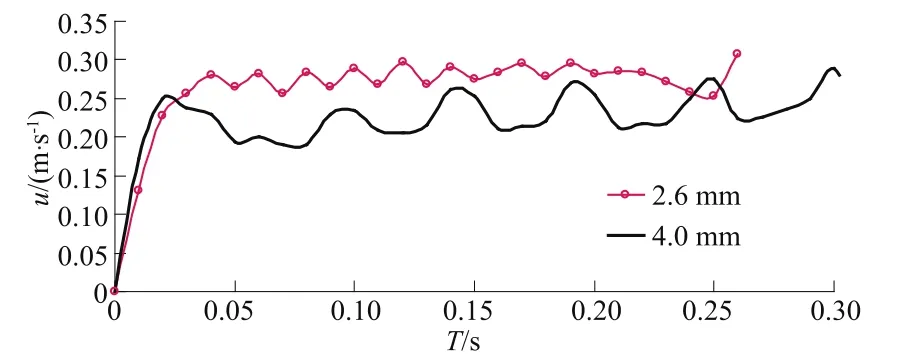
图4 气泡速度随时间变化关系Fig.4 Curves of bubble rising velocity versus time
将试验结果[6]与数值模拟得到的结果进行了对比,结果见图5。从图5中可以看出,气泡的上升经历了从加速到速度在固定值上下振荡的过程。气泡速度在经历数个较强烈的振荡周期后逐渐趋于平缓,认为达到终速度水平。试验值在早期的上升速度值都比模拟值大一些,原因可能是因为试验采用的水中有杂质以及温度等因素的干扰影响,模拟采用的均为标准状态下的纯水以及假设模拟的工况均处于恒温状态。在气泡终速度上模拟值和实验室吻合良好,均呈现有规律的围绕速度平均值上下振荡。

图5 气泡速度随上升高度变化关系Fig.5 Curves of bubble rising velocity versus height
一些学者指出气泡形状和速度的振荡可能是受到其表面的涡脱落强迫引起的[7],也有学者提出是由于气泡脱离发生装置时的动摇引起的[8]。关于气泡上升运动变形的原因,也或许是由多方面因素共同决定的,这个问题无疑需要更进一步的探索。
4 结 论
本文以水为工作介质,对静水中单个气泡的动力学特性进行了数值模拟,得到以下结论:
(1)计算了气泡的变形过程、路径和上升速度等参数,并且与试验值吻合。
(2)气泡的速度曲线呈现围绕一个固定值上下振荡的状态,并且振荡幅度随着气泡直径的增大而增大。
(3)本文采用的算法可以有效地模拟水气交界面,可以为水中气液两相流的研究提供一种可行的模拟方法。
[1] CLIFT R,GRACE JR,WEBER M E.Bubbles,Drops and Particles[M].New York:Academic Press,1978:172.
[2] TSUGE H.Hydrodynamics of Bubble Formation from Submerged Orifices[M].Encyclopedia of Fluid Mechanics Vol.3.Houston:Gulf Publishing,1986:191-232.
[3] TOMIYAMA A,YOSHIDA A,HOSOKAWA S.Surface Tension Force Dominant Regime of Single Bubble Rising Through Stagnant Liquid[C]∥The Japanese Society for Multiphase Flow.Proceedings of the 4th UK-Japan Seminar on Multiphase Flow.Cambridge,UK,2001.
[4] OKAWA T,TANAKA T,KATAOKA I,et al.Temperature Effect on Single Bubble Rise Characteristics in Stagnant Distilled Water[J].International Journal of Heat Mass Transfer.2003,46:903-913.
[5] HIRT C W,NICHOLS B D.Volume of Fluid(VOF)Method for the Dynamics of Free Boundary[J].Journal of Computational Physics,1981,93:201-225.
[6] 白云艳.静水中运动气泡变形特性的测量研究[C]∥水利量测技术论文选集(第七集).郑州:黄河水利出版社,2010:183-189.(BAIYun-yan.Measurement of the Deformation of Rising Bubbles in Stagnant Water[C]∥Proceedings of the Hydraulic Measuring Technique(Vol.7).Zhengzhou:The Yellow River Water Conservancy Press,2010:183-189.(in Chinese))
[7] MARCO P D,GRASSIW,MEMOLI G.Experimental Study on Rising Velocity of Nitrogen Bubbles in FC-72[J].International Journal of Thermal Sciences,2003,42(5):435-446.
[8] EDGERM,GRANTCD.The Terminal Velocity and Frequency of Oscillation of Drops in Pure Systems[J].Chemical Engineering Science,1971,26(7):1001-1012.
(编辑:曾小汉)
Numerical Simulation of the Dynam ics of Single Bubble Behavior in StillW ater
XU Ling-jun1,CHEN Gang1,SHAO Jian-bin1,XUE Yang2
(1.College ofWater Conservancy and Hydropower Engineering,Xi’an University of Technology,Xi’an 710048,China;2.State Key Laboratory of Hydraulics and Mountain River Engineering,Sichuan University,Chengdu 62002,China)
To study the dynamic properties of bubble rising in thewater,a simulationmodel of single bubble under buoyancy and gravity in stillwater was established by CFD software.Taking hydrostatic pressure gradient into consideration,the no-slip technology was applied to dealwith the boundary of flow field,and thewhole structured grid technology was used to dealwith the bubble and still water area.Using thismodel,bubbles of 2.6 mm and 4mm diameterswere simulated to analyze themovementmechanism of the bubbles in still water.The numerical results were further compared with the test data.The rising route and velocity were well consistentwith the test data.The approach in this study offered an effective solution to investigate the dynamic properties of bubble in water.
bubble;numerical simulation;movementmechanism
TV131.4
:A
1001-5485(2011)09-0018-03
2010-10-07
国家自然科学基金(50579085)
徐玲君(1983-),女,四川眉山人,博士研究生,主要从事流体力学研究,(电话)13572530194(电子信箱)xulingjun@163.com。
