边坡工程模糊随机可靠度分析
2011-09-05宋新龙余宏明
王 宇,宋新龙,张 行,汪 灿,余宏明
(1.中国地质大学(武汉)工程学院,武汉 430074;2.中铁西北科学研究院有限公司,兰州 730000)
边坡工程模糊随机可靠度分析
王 宇1,宋新龙2,张 行1,汪 灿1,余宏明1
(1.中国地质大学(武汉)工程学院,武汉 430074;2.中铁西北科学研究院有限公司,兰州 730000)
将模糊随机理论应用于边坡可靠性评价当中,为了考虑随机变量的模糊随机性,引入稳定系数的隶属函数对边坡的实际工作状态进行模糊可靠评价。提出模糊随机极限状态方程的二次构造思想,即将模糊随机理论和响应面法相结合,首先利用响应面法进行一次构造,得到可靠度响应面函数,在此基础上借助隶属函数的补函数作为辅助,进行二次构造极限状态方程来计算边坡的模糊随机可靠度。结果表明,该方法计算简便、收敛速度快,克服了对模糊概率密度函数直接积分求解时过程复杂、耗费机时的缺点,具有较高的计算精度和广泛的工程实用性。计算所得到的可靠性指标更加能够真实地反映边坡的稳定状态,为边坡工程可靠性研究提供了一种新的方法。
模糊可靠度;响应面法;隶属函数;功能函数;可靠性指标
边坡工程的稳定可靠性问题一直是岩土工程领域的一个研究热点,边坡稳定性分析经历了以单一稳定系数Fs来衡量稳定性的定值法和考虑岩土体参数随机性的概率分析法,但是岩土工程中不仅存在随机性,还存在着大量的模糊性。边坡稳定和失稳之间存在着一个模糊过渡区。边坡稳定模糊随机可靠度的研究已有了一定的进展,国内外学者已经作了一些相关性研究工作,并取得了一定成就[1-6],但是模糊理论与可靠度结合在边坡工程中的应用仍然存在许多问题,比如边坡模糊评价标准的建立、随机过程隶属函数的建立等,其中比较突出的问题是极限状态变量模糊随机可靠度的求解问题,因为它直接影响着边坡稳定评价尺度的正确与否。以往常常通过构造模糊破坏概率函数,对随机变量进行模糊处理,然后进行数值积分求解,计算难度大,过程复杂,计算时相当耗费机时,尤其当被积表达式为多元函数时,直接计算多重积分得到可靠性指标显得更为困难。在前人研究的基础上,本文将响应面法(RSM)与模糊随机可靠度理论相结合,计算边坡的模糊随机可靠度指标,该方法避免了传统计算方法的缺陷,为边坡工程可靠性分析的理论与工程实践提供了一条新的途径。
1 模糊随机极限状态方程构造
1.1 基于RSM法功能函数一次构造
RSM方法根据各种试验结果,采用统计推断的方法对极限状态方程在验算点附近进行重构。用RSM法重构复杂结构的近似功能函数,就是设计一系列变量值,每一组变量值组成一个试验点,然后逐点进行结构数值计算,得到对应的一系列功能函数值,通过这些变量值和功能函数值来重构一个明确表达的函数关系。
在边坡稳定可靠度分析中,通常结合传统的稳定系数法来处理,即可得到边坡稳定可靠度分析的功能函数为

式中:X为随机参数;G(X)为功能函数;Fs(X)为稳定系数方程。由于功能函数G(X)无法明确表达,根据响应面法可以用一个近似多项式g(X)作为响应函数去代替真实的功能函数,因此式(1)可以表示为

响应函数的形式要满足2个要求:①其数学表达式在基本能够描述真实函数的前提下要尽量简单,以避免可靠性分析过于复杂;②响应函数中应设计尽可能少的待定系数以减少分析的工作量。同时满足这两方面要求时以多项式为最佳。文献[7]提出了含一次项以及二次交叉项的响应面函数,但经对比发现带交叉项的与不带交叉项的二次多项式精度差异不大[8,9],而后者计算量要远远小于前者。基于以上考虑,本文采用不带交叉项的二次多项式作为响应面函数,可表示如下:

式中:xi为随机变量;a,bi,ci为待定系数。
利用响应面法完成边坡模糊随机分析功能函数的第一次构造过程如下:
(1)确定分析中所要考虑的随机变量。在确定每一个随机变量在试验点的取值时,一般考虑每个随机变量都有4个值,分别是均值μi、方差σi和μi±σi。在目前的分析计算中,通常取m=1,将g(μi,…,σi±μi,…,σi)代入式(3)就得到2n+1个方程。
(2)用边坡稳定分析的程序,求得每一试验点(μi,…,σi±μi,…,σi)所对应的稳定系数。
(3)将每一试验点所对应的稳定系数值及相应的随机变量的值代入到由第二步产生2n+1个的方程中,这样就得到了一个方程组,解线性方程组,就可以求得a,bi,ci。再将每一个系数代入式(3)就得到了所要求的响应面函数,从而也就完成了稳定系数极限状态方程的第一次构造。
1.2 基于模糊理论的功能函数二次构造
在边坡可靠性分析中,即使基本随机变量仅具有随机性,但其破坏失稳准则是模糊不明确的,边坡的破坏可以看作为一个随机事件,边坡的可靠度就是模糊随机事件的概率。
由于边坡失稳破坏的模糊性,使得功能函数Z=g(X)的值仅反映了边坡稳定性适用程度的大小,其变化表示了边坡稳定适应性的损益。认为,Z>0不表示边坡完全处于可靠状态,Z<0并不意味着边坡完全破坏,Z=0也不是边坡可靠和破坏的失稳状态界线。
考虑边坡由“完全失稳”到“完全稳定”之间的中间过渡性时,引入可以表征边坡稳定性的隶属函数μz。当μz→0时,表示边坡极不稳定,失稳的可能性很大;当μz→0.5时,表示边坡处于极限状态,边坡稳定和失稳的可能性都为0.5;当μz→1时,表示边坡很稳定,失稳的可能性很小[10]。
设边坡破坏失稳的模糊随机事件可表示为

式中z∈Ω是模糊随机事件空间中的状态随机变量。
若Z的概率密度函数为fz(z),根据模糊数学理论可定义边坡破坏事件的概率为

式中μE(z)为边坡失稳隶属函数,应为递减函数,使边坡的破坏程度随稳定系数的增大而减小。
设基本随机变量X的联合概率密度函数为fx(x),则边坡破坏事件E的概率可表示为
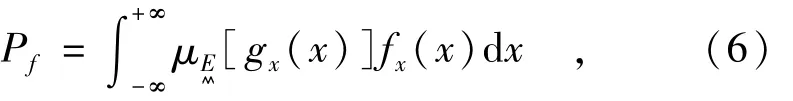
若X是独立随机变量,式(6)又可写成

直接计算式(6)和(7)的多重积分得到边坡的可靠性指标比较困难,下面介绍隶属函数补函数这一思想来解决这一问题。
边坡稳定系数隶属函数μE(z)为递增函数,则相应边坡失稳时的破坏隶属函数μE(z)应为递减函数,即随着稳定系数的增大,破坏概率变小,且0≤μE(z)≤1,因此可将1-μE(z)看做随机变量Xn+1的累 积分布函数F(x)。于是式(6)变为
xn+1n+1

其中新的随机变量Xn+1的累积分布函数和概率密度函数分别为:

上述做法把隶属函数的补函数视为一个新随机变量的累积分布函数,类似于非正态随机变量的当量化,具有一定的普遍性。其实在式(9)中,也可以直接令FXn+1(xn+1)为标准正态分布函数ø(xn+1),相应地式(10)中的fXn+1(xn+1)为标准正态概率密度函数φ(xn+1),类似于映射变量法的处理,则所得的Xn+1为标准正态分布变量。
由式(8)可知,边坡模糊随机可靠度问题的失效域为{x|gx(x)≤xn+1},因此相应的等效功能函数为
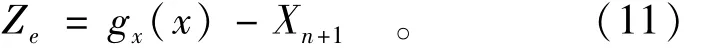
于是,式(11)右侧等于0即为模糊极限状态方程,以式(9)和(10)为补充条件,可以利用经典可靠度分析方法计算模糊随机可靠度。
2 稳定系数隶属函数的确定
在缺乏对边坡的影响因素深入彻底地认识之前,简单地以某一稳定系数为依据来判断边坡的稳定或失稳的状态显然是不合理的,其次,如果直接考虑因素的模糊随机性,假设一种有界模糊数,其核值、最大容许区间以及隶属函数线型的确定等关键问题都是由主观决定的,缺乏客观依据。因此,从稳定系数隶属函数这一角度出发来研究边坡的稳定可靠性应该更加科学合理。
稳定系数的隶属函数的具体形式直接影响边坡稳定性评价结果,因此隶属函数的构造在边坡稳定模糊随机可靠度分析中显得至关重要。结合边坡的实际情况,一般来说,稳定系数越大则边坡稳定的可能性越大,并且当稳定系数由小到大变化时,对边坡状态的判断也存在从容易(失稳)到困难(模糊平衡)再到容易(稳定)的变化过程。这要求稳定系数的隶属函数是单调升函数,且其曲线的斜率随着安全系数的增大先单调增大然后再单调减小。
本文从常见隶属函数中选取,并结合前人的研究成果[11-14],选用戒下型岭形分布函数作为边坡稳定系数的隶属函数,其函数表达式为
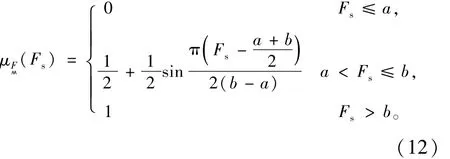
式中a,b为待定系数,稳定系数小于a的边坡绝对破坏,大于b的边坡绝对稳定,等于(a+b)/2时状态最模糊。
3 工程应用分析
3.1 研究区概况
杭兰高速公路枞树坪边坡位于重庆市巫山县两坪乡桂花村境内,长约300 m,呈约262°走向沿溪沟南侧山坡展布。边坡出露地层岩性,上覆为第四系全新-更新统残坡积含碎石亚黏土:褐黄、灰黄色,湿,硬塑状,含10%~20%的碎石、角砾,钻探揭露上覆残坡积堆积层厚度12~26.90 m,结构不均,稳定性较差;下伏基岩为T2b3泥灰岩,岩层产状189°∠34°,岩层倾向与自然边坡坡向反向斜交。边坡土体的重度采用天然状态下γ=21 kN/m3,饱和状态下γ=25.6 kN/m3。滑带土抗剪强度天然状态下取c=29.6 kPa,φ=23.5°,饱和状态下取c=14.4 kPa,φ=13.2°。滑带土抗剪强度统计见表1。
3.2 功能函数一次构造
根据极限状态方程二次确定思想,首先由响应面法拟合二次函数进行功能函数的一次构造。在计算稳定系数时,采用有限元强度折减法求解,按照平面应变问题建立模型。岩土材料用二维实体结构单元六结点三角等参单元T6,按照连续介质处理,采用理想的弹塑性模型。典型的边坡最大剪应变和最大水平位移云图见图1和图2。天然工况和饱水工况下稳定系数计算结果见表2。

表1 滑带土抗剪强度参数统计表Table 1 Shear strength parameters of soil from the sliding zone

图1 边坡最大剪应变图Fig.1 M aximum shear strain of slope

图2 边坡最大水平位移云图Fig.2 M aximum horizontal displacement of slope

表2 稳定性计算结果Table 2 Results of stability calculation
据稳定性计算结果,根据上文所述的响应面法便可构造出边坡天然状态和饱水状态下的响应面函数。
3.3 功能函数二次构造
为了尽量减少人为因素给分析结果带来的主观影响,本文利用杭兰高速公路上27个边坡稳定系数统计资料构造模糊约束条件,来确定戒下型岭形分布隶属函数中的待定系数。经过野外实地调查和室内深入的研究发现,稳定的边坡中,稳定系数最小为0.84,即安全系数小于0.84的边坡不可能再处于稳定状态,隶属度为0;在破坏的边坡中,稳定系数最大则达到了1.62,即稳定系数大于1.62的边坡不可能再破坏,隶属度为1。求得了稳定系数的隶属函数后,相应的则可以得到边坡失稳破坏时的隶属函数
于是可令a=0.84,b=1.62,此时有(a+b)/2=1.23,于是稳定系数的隶属函数可确定为

为了使用上文所提的模糊理论对功能函数进行二次构造,由隶属函数模糊算子的运算性质,反求了边坡破坏时的隶属函数,函数采用戒上型岭形分布,其函数曲线与戒下岭形互补,表示为

采用隶属函数补函数法,引入新的随机变量X3,由此来构造边坡失稳隶属函数的补函数。由式(9)和式(10)知,新的随机变量X3的概率密度函数和累积分布函数分别为:

黏聚力c、内摩擦角φ参数统计已知,进一步可求得新随机变量X3的均值和方差,从而可以构造形如式(11)的极限状态方程。
3.4 计算结果及分析
利用最终得到的功能函数对二种工况下的边坡进行可靠性评价,可分别求得该高边坡在天然状态和饱水状态下的模糊随机可靠度指标,并按随机参数为正态分布时给出的失效概率,计算时采用一次二阶矩法。为了便于说明计算结果的可靠性,同时计算了传统模糊可靠度和不考虑稳定系数隶属函数情况下的可靠度指标,见表3。
由表3的计算结果可知,常规的边坡可靠性分析方法由于没有考虑随机变量模糊性对失稳概率的影响,得出的破坏概率过小,过大地估计了边坡的稳定可靠状态;功能函数二次构造法的计算结果和直接数值积分得出结果相差很小,这说明了二次构造法符合计算精度要求。为了便于和以往的可靠性指标直接积分法相对比,本文仅考虑了随机变量的正态分布类型。边坡模糊随机可靠度分析,以考虑随机变量模糊容许区间等价于稳定系数隶属函数的模糊化处理,用这种方法评价边坡的实际状态,将更加科学合理,符合客观事实。

表3 可靠性计算结果Table 3 Results of reliability calculation
4 结论及建议
本文将模糊随机理论引入边坡可靠性评价中,既考虑了因素的随机性,同时也考虑了因素的模糊性,使边坡可靠性评价结果更加客观、真实。应用响应面法耦合模糊随机理论构造可靠性功能函数,避免了传统方法的缺点,计算效率高,结果可靠,具有广泛的应用前景和工程价值。边坡模糊随机可靠性分析的难点问题是稳定系数隶属函数的选取,评价的合理性很大程度上取决于边坡稳定隶属函数确定的正确性。然而隶属函数的准确确定不太现实,由边坡实例的统计结果作为模糊约束的土坡稳定隶属函数表达式仍然包含很多人为因素,需要更多的工程实例的检验和修正。
[1] DODAGOUDAR G R,VENKATACHALAM G.Reliability Analysis of Slopes Using Fuzzy Sets Theory[J].Computers and Geotechnics,2000,27(2):101-115.(in Chinese)
[2] 李彰明.模糊分析在边坡稳定性评价中的应用[J].岩石力学与工程学报,1997,16(5):491-495.(LI Zhang-ming.Application of Fuzzy Analysis in Slope Stability Evaluation[J].Chinese Journal of Rock Mechanics and Engineering,1997,16(5):491-495.(in Chinese))
[3] 李文秀.岩土边坡稳定性的模糊测度分析[J].岩土工程学报,1996,18(2):11-16.(LIWen-xiu.Fuzzy Measure Analysis for the Stability of Rock and Soil Slopes[J].Chinese Journal of Geotechnical Engineering,1996,18(2):11-16.(in Chinese))
[4] 谭晓慧.边坡稳定分析的模糊概率法[J].合肥工业大学学报(自然科学版),2001,24(3):443-446.(TAN Xiao-hui.The Stability Analysis of Slope by Fuzzy Probability Method[J].Journal of Hefei University of Technology,2001,24(3):443-446.(in Chinese))
[5] 楼 芬,邓 建.AHP-FUZZY法在露天矿边坡稳定性分析中的应用[J].采矿技术,2008,8(2):28-30.(LOU Fen,DENG Jian.The Application of FUZZY AHP Method in the Slope Stability Analysis of Open-Pit Mine[J].Mining Technology,2008,8(2):28-30.(in Chinese))
[6] 徐卫亚,蒋中明,石安池.基于模糊集理论的边坡稳定性分析[J].岩土工程学报,2003,25(4):410-413.(XU Wei-ya,JIANG Zhong-ming,SHI An-chi.Slope Stability Analysis Using Fuzzy Sets Theory[J].Chinese JournalofGeotechnical Engineering,2003,25,(4):410-413.(in Chinese))
[7] GAYTON N,BOURINET JM,LEMARIE M C.A New Statistical Approach for Structural Reliability Problem[J].Structure Safety,1990,7(1):57-66.
[8] 苏永华,赵明华,蒋德松,等.响应面方法在边坡稳定可靠度分析中的应用[J].岩石力学与工程学报,2006,25(7):1418-1424.(SU Yong-hua,ZHAO Ming-hua,JIANG De-song,et al.Application of Response Surface Method to Reliability Analysis of Slope Stability[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(7):1418-1424.(in Chinese))
[9] RAJASHEKHAR M R,ELLINGWOOD B R.A New Look at the Response Surface Approach for Reliability A-nalysis[J].Structure Safety,1993,12(3):205-220.
[10]徐 辉.基于模糊集理论的边坡稳定模糊随机可靠度分析[D].杭州:浙江大学,2006.(XU Hui.Fuzzy Reliability Analysis of Slope Capacity Based on Fuzzy Sets[D].Hangzhou:Zhejiang University,2006.(in Chinese))
[11]冯夏庭.智能岩石力学导论[M].北京:科学出版社,2000.(FENG Xia-ting.An Introduction to Intelligent Rock Mechanics[M].Beijing:Science Press,2000.(in Chinese))
[12]GIASIC I,MASIP,CHERUBINIC.Probabilistic and Fuzzy Reliability Analysis of a Sample Slope Near Aliano[J].Engineering Geology,2003,67(3-4):391-402.
[13]李胡生.岩土参数随机-模糊统计中的隶属函数形式[J].同济大学学报,1993,21(3):362-368.(LI Hu-sheng.On the Membership Functions in a Random-Fuzzy Statistics Method for Geotechnical Parameters[J].Journal of Tongji University,1993,21(3):362-368.(in Chinese))
[14]祁生文,伍法权,刘春玲,等.地震边坡稳定性的工程地质分析[J].岩石力学与工程学报,2004,23(16):2793-2797.(QI Sheng-wen,WU Fa-quan,LIU Chunling,et al.Engineering Geology Analysis on Stability of Slope under Earthquake[J].Chinese Journal of Geotechnical Engineering,2004,23(16):2793-2797.(in Chinese) )
(编辑:曾小汉)
Fuzzy Stochastic Reliability Analysis of Slope Engineering
WANG Yu1,SONG Xin-long2,ZHNAG Hang1,WANG Can1,YU Hong-ming1
(1.School of Engineering,China University of Geosciences,Wuhan 430074 China;2.Northwest Research Institute Co.,Ltd of C.R.E.C,Lanzhou 730000)
Fuzzy stochastic theory is applied to the slope reliability evaluation.Considering the fuzzy and stochastic features of random variables,the subordinate function of stability factor is introduced to perform fuzzy reliability analysis for the actualworking condition of the slope.The secondary structure of fuzzy random limit state equation is proposed on the basis of combining the fuzzy stochastic theory with the response surfacemethod.The response surfacemethod is used on a structure firstly to obtain the reliability response surface function,based on which the complementary function of subordinate function is used as an auxiliary to carry on the secondary limit state equation to calculate the random fuzzy reliability of the slope.Rather than directly solving the fuzzy probability density function by integral calculus,which is complicated and time-consuming,thismethod is proved to be simplewith fast convergence and high precision of calculation,thereby can be used widely.The slope stability can be reflectedmore accurately by the calculated reliability indexes.Themethod can be regarded as a new approach of studying the reliability of slopes.
fuzzy reliability;response surfacemethod;subordinate function;performance function;reliability index
P642
:A
2010-10-15;
2011-05-03
国家“十一五”科技支撑计划项目(2008BAC47B0);交通部西部交通建设科技项目(200906)
王 宇(1985-),男,河北沧州人,硕士研究生,主要从事边坡稳定性分析及边坡与滑坡工程治理设计等方面研究,(电话)13720184614(电子信箱)good541571889@126.com。
