色谱经济分析法置换系列研究:分配比
2011-09-05毛锴苑李跟强游士兵
沈 萍,张 佩,毛锴苑,李跟强,游士兵
(1.武汉职业技术学院生物工程学院,武汉 430074;2.武汉大学 经济与管理学院,武汉 430071)
0 引言
在对经济色谱分析方法有了研究具体框架的基础上(游士兵,2011),对其各个环节的深入研究和经济学置换将是后续研究的重点。色谱分析法的原理是组分在固定相和流动相间进行反复多次的“分配”,由于分配比K(或容量因子k)的不同而实现分离。事实上,分配比的差异是所有色谱分离的实质性因素。基于此,本文拟对色谱经济分析法中的分配比进行初步探究,以期为后续色谱经济分析法的各种概念和方法的置换奠定一定的基础。
1 色谱经济分析中分配比的置换
1.1 置换的可行性分析
在定义色谱经济分析方法中的分配比时,我们必须再次明确经济中固定相和流动相的定义。我们认为,固定相是对组分有吸附作用或者说阻止流动相的推动作用的因素,流动相是对组分有推动作用或者说具有克服固定相的吸附作用,他们对于组分的影响是对立的,反向的。
与复杂的化学混合物不同,在复杂经济现象中每一类事物都具有其偶然性、特殊性和随机性,共同影响着系统整体,但是这种影响并非完全是杂乱无章、无规律可循的。每一个体仍然是围绕某个“定值”波动的,这一“定值”就是客观事物的一般性、必然性和趋势性。倘若将这些波动因素以函数形式表达,进而收集统计数据并进行处理,这些“定值”就能在一定程度上体现复杂经济现象中的一般规律,即经济学中的“分配比”。
在通常情况下通过对大量经济现象数据的统计处理与分析,这种反应规律可以进行回归分析得到大致合理的无偏估计。所以分配比定义从化学类比到经济中具有很大的可行性。通过经济学分析和回归模型得到的分配比,既然是复杂经济现象中的一般规律,那么在相似的同类经济对象与相近的时空环境下,其具有一定的参考作用甚至可以直接引用。
当选取最优固定相与流动相,即满足所选取的固定相(混合固定相)与流动相(混合流动相)对待分离的经济对象起关键或核心的作用;所选取的固定相与流动相对待分离的经济对象具有相反的作用效果;所选取的固定相与流动相不相关,或者即使相关也是极低程度的相关;固定相与流动相对于待分离经济对象的作用效果(或影响程度)是相对稳定的,即可通过定量分析获得;固定相与流动相对不同组分的分配比要有显著的差别。
1.2 分配比的定义
在化学领域中,色谱分析利用混合物中各物质在两相间分配比的差别,当溶质在两相间做相对移动时,各物质在两相间进行多次分配,从而使各组分得到分离。由于不同组分的分配比存在差异,分配比大的组分在固定相上的溶解或被吸附的比例大,因此在柱内的移动速度慢。反之,分配比小的组分在固定相上的溶解或被吸附的比例小,在柱内的移动速度快。若两组分的分配比存在微小的差异,经过反复多次的分配平衡,使微小的差异积累起来,其结果就使分配比不同的组分被先洗脱,从而使两组分得到分离。所以,分配比的差异是所有色谱分离的实质性的原因。分配比被定义为在一定温度下,溶质在互不混溶的两相之间质量之比。即分配比为

不妨假设待分离对象通过色谱分析过程,固定相与流动相对其反应的综合反应为F(x1,x2),其中x1为固定相,x2为流动相。那么通过一系列的样本数据(包括F、x1、x2),通过回归模型,可以得到

故/=k,即经济色谱分析中的分配比。需要指出的是,质量是化学中衡量物质属性的重要因素或基本因素。在化学中,进行的均是物质分离,但经济领域中的分配比有其自身的特点,它不再只是某一个确定因素在固定相和流动相作用下的比例,而是根据所要分析的具体问题来定。例如,当我们需要对不同的消费群体进行分离时,分配比可能是固定相和流动相中的消费者个数比;当我们需要对不同规模的企业进行分离时,分配比可能就是固定相和流动相中企业的产值比。而在化学领域中,均只是质量比。
在化学领域分配比的大小是随多种外在因素的改变而变化的,但在确定条件下,分配比可先由实验测出并作为已知条件。在进行具体实验时,若保持相同的条件,就能够根据组分已知且不同的分配比将其分离。在经济领域中,大多数经济现象在某一相对稳定的外界条件下具有某种规律或性质。待分离的经济现象对于两种或多种经济行为会呈现出稳定的反应规律,这种反应变化可以是正相关,也可是负相关的。可以认为,经济现象中的不同组分反应规律的不同是其分配比不同的外在体现。那么,根据其不同的反应规律(即分配比),我们可以将不同的经济现象加以分离。
1.3 分配比与分配系数
在化学液相色谱分离中,分配比常以分配系数为表现形式。分配系数是组分在固定相和流动相之间的浓度之比,若两相体积已知(很容易获得此条件),就可以得到相应的分配比。所以,分配系数是分配比的间接表现形式。
在经济领域中,很多经济规律在某一时间序列的演变或在某一横截面的比较中才能得到体现与总结。此时,我们旨在研究的分配比将会与时间或空间结合,以单位时间的组分或单位空间的组分为间接表现形式。我们不妨认为,在经济中分配系数是分配比具体的表现形式。由此,化学与经济在分配比和分配系数的概念能够实现统一。
1.4 分配比性质的探讨
(1)分配比表现的是固定相和流动相对待分离组分的作用力大小,若分配比大于1,则说明固定相对组分的作用大
k=组分在固定相中的质量 组分在流动相中的质量
置换到经济中,分配比是固定相对组分的作用与流动相对组分的作用的比值,利用固定相、流动相对组分的作用差别,让组分在固定相、流动相中反复作用,不同组分在固定相、流动相中的差异逐渐累积,使不同组分逐渐分离,最终达到分离的效果。所以,在定义固定相和流动相的基础上,我们可以将经济分配比定义为在一定的经济环境下,所选取的固定相和流动相对于被分离组分的作用大小之比。于流动相;若分配比等于1,则说明固定相对组分的作用等于流动相;若分配比小于1,则说明固定相对组分的作用小于流动相。
下面我们考虑两种极端的情况。若分配比为正无穷,即固定相对该组分的作用远大于流动相,在化学中,这种组分只能被留在柱内,没有相应峰形,似乎在化学中这种分配比是没有意义的。但是在经济学中,根据前面固定相和流动相的定义(我们将固定相看做是阻碍其进行外在表现、有所作为的因素;反之,流动相是促进其进行外在表现、有所作为的因素),我们不妨认为这是一种不作为的情况,是一种特殊经济主体或经济行为类型。需要指出的是,在固定相和流动相中不作为的物质中也可能是含有多种不同的组分,这在我们以后的研究中可以有所深入。若分配比为零,即流动相对组分的作用远大于固定相,这与分配比为正无穷大时的情况正好相反,说明在该分配比的条件下经济总体或经济行为难以分离。
从分配比的这两种极端情况来看,固定相和流动相选择的重要性便有所显现,一方面倘若我们选取的固定相或流动相对于被分离总体中的任意组分而言,分配比都是等于正无穷或零的话(我们不能排除这种情况的发生),则分离就完全失败。但是在经济学中,由于经验以及所得数据等原因,会让我们减少犯这类错误的概率。就如同在化学中,我们对某些物质的属性多少有所了解一样。另一方面不同组分有不同的分配比,更重要的是不同组分的分配比的差异是否是足够显著,倘若我们分离混合在一起的两个组分,其中一个组分分配比是正无穷,另一个组分的分配比是零,那它们就很容易被分离出来。
(2)分配比的连续性和非连续性。在化学中,每一种组分的分配比不相同,不存在分配比连续的情况。对于非连续的情况,我们能够根据色谱分析的原理进行很好的分离,但是在经济中分配比可能连续,如当我们对消费群体进行分类时,固定相和流动相对每个消费个体的分配比可能都是不同的。这种连续的情况就亟待我们进行更深一步的研究。
(3)分配比的参照。分配比决定峰的形状,若已知某组分在某一固定相和流动相中的分配比是1:1,那么在相同固定相和流动相下,可以将分配比为1:1的组分的峰形作为参照,来判断分配比未知的组分的分配比与1的相对大小,即固定相与流动相间作用力大小关系。
(4)分配比的未知性和已知性。在化学中,我们在对物质进行分离时,通常情况下在温度、压强等确定的条件下固定相和流动相对其组分的作用的大小,即分配比是已知的;当然也存在分配比未知的情况,通过最后显现的峰来判断不同组分的分配比大小。同理,在经济分析中,有一些组分的分配比我们是已知的,如通过具体的实践调查所得,但是将这些经济行为或者经济主体混在一起时,我们只知道其中存在着哪一些的分配比,这时任务便是将不同分配比的组分分离出来;有一些组分的分配比是未知的,可通过分离的结果得到该分配比,不同的分配结果即对应着不同的分配比。在我们进行初次试探性实验或者多次试探性实验后,可以得到相应的客观经验,形成较稳定的体系,从而促进进一步实践。
2 经济领域的分配比的模拟计算实例
根据对流动相与固定相的置换与定义,流动相是对分配组分起促进作用的因素,固定相是对分配组分起阻碍作用的因素。
在化学中分配系数为
k=组分在固定相中的浓度 组分在流动相中的浓度分配比为
k'=组分在固定相中的质量 组分在流动相中的质量
不同组分在固定相和流动相中具有不同的分配系数和分配比,换言之,固定相和流动相对不同组分具有不同的吸附能力。
2.1 价格收入弹性下的分配比模拟计算
从化学科学映射到经济科学中,一般弹性是度量敏感度的一个重要指标。
关于固定相与流动相及消费者行为的置换如图1、2。
在一定温度、压强下,假定:
(1)个人偏好在短时间不会改变;
(2)经济社会不会出现大幅的变动而造成非理性消费;
(3)对经济状况理性预期等。
对消费者群体来说,消费量是价格与收入的函数,即

两边取对数后,有

两边微分,有

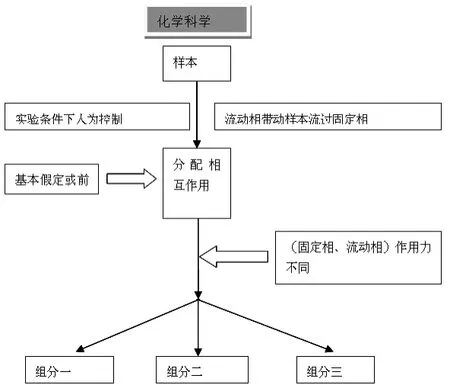
图1

图2
考虑到消费量的价格弹性一般是负值,消费量的收入弹性一般为正值,即

也就是价格是对消费量的逆指标,收入是对消费量的正指标,故设定价格是固定相,收入是流动相。
需要说明的是,在化学中的固定相和流动相在已知待分离物质的前提下即实验前就可以基本确定,经过检测后可对固定相和流动相的组成进行再调整。而在经济学中,通常需要我们进行初次试探性实验或者多次试探性实验,进而确定流动相与固定相。
对于化学科学与经济学科的数据获取及处理的置换,由于化学在一定温度、压强下,样品的化学性质比较稳定,化学实验具有重现性,即不同的人在相同的实验条件下,采用相同的实验步骤就会得到相同的实验结果,而经济社会科学中,影响的因素太多且不可控,即使同一个人此时与下一时刻对外界环境的反应都可能有很大不同,即具有随机性,而解决随机性的有效方法就是统计回归,这样使干扰项的均值(期望值)为0,对解释变量不会造成系统性的影响。化学科学与经济科学的对比置换如图3。
构造消费量函数模型为
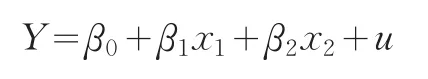
针对消费者行为我们选取模型

其中,Y代表消费量,x1代表价格水平,x2代表收入水平。
理论上,我们有
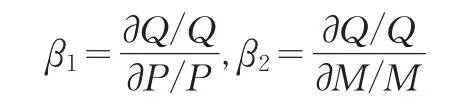

图3
那么,在此经济分类中的分配系数K=β1β2,表现为消费量的价格弹性β1与收入弹性β2的比值。如果我们获取的价格与收入的数据分别处于不同的时间段,例如:价格的年变化和收入的月变化,那么需要对该K值进行调整,转化为相同期间里的平均变化,进而算出相应的分配比′,′是体现了价格弹性β1和收入弹性β2两种因素的综合指标,根据′值所处的不同区间,将消费者分成不同的群体。
当需要对消费者个体分类时,可以选取消费者的时间序列的消费情况资料,根据不同年份的价格水平和收入水平回归得出消费量的价格弹性β1和收入弹性β2,此时假定消费者偏好在所选取的时间区间内没有明显变化;当需要对消费者群体以区域划分时,可以选取不同区域在一定的价格水平和收入水平下消费者的消费情况资料,比如横截面数据或是面板数据,进行回归得到不同区域的消费者整体弹性的不同。
2.2 边际消费倾向下的分配比模拟计算
下面我们只针对收入变化而不考虑价格变化的影响,对消费者进行分类。
考虑到储蓄倾向会抑制消费者的消费行为,而消费倾向会促进消费者的消费行为,故我们设定储蓄倾向为固定相,消费倾向为流动相,对消费者进行分类。
固定相:储蓄倾向
流动相:消费倾向


表1 数据模拟
其中,α为边际储蓄倾向,β为边际消费倾向。下面我们进行数据模拟(见表1),用实例说明色谱分析在消费者分类中的应用。
从表1可以看出,尽管消费者1、3、5、9收入变化不尽相同,但他们却表现出相同的边际消费倾向和边际储蓄倾向,消费者2、4、8也是如此,按照上文中定义的分配比可以将这10位消费者分为四组,1、3、5、9为一组,2、4、8为一组,6、10为一组,7单独为一组。
随着样本容量的扩大,计算得到的分配比具有连续性,即0到1之间两位小数都可能取到,为了使分类不至于过细,我们可以设定不同区间,比如(0,0.30)、(0.31,0.40)、(0.41,0.60)、(0.61,0.70)、(0.71,0.80)、(0.81,0.90)、(0.91,1.00),落在同一个区间的消费者我们认定具有相似的边际消费倾向。
3 结语
本文着重分析化学色谱分析中的分配比在经济学中的概念置换与应用研究,基于科学的理论研究和置换分析,得出了分配比在经济分类中的可行性与有效性。我们的初步研究还存在诸多不成熟的地方,尚待深入全面多层次的研究。但是,经济色谱分析充分结合了定性与定量分析,其优越性和实践性预示着其在经济学研究中是科学有效的方法。
[1]游士兵,吴比,沈萍,梅敏,苏正华.复杂经济现象分类方法创新的理论前瞻——基于化学“色谱分析法”的借鉴与思考[J].统计与决策,2011,(7).
[2]游士兵,梅敏,吴比.色谱分析法在经济领域中的应用展望[J].统计与决策,2011,(11).
[3]詹姆斯·蒙蒂尔.行为金融:洞察非理性心理和市场[M].北京:中国人民大学出版社,2003.
[4]张祥民,现代色谱分析[M].上海:复旦大学出版社,2004.
[5]傅若农.色谱分析概论(第2版)[M].北京:化学工业出版社,2005.
[6]张维平,高娟,白泉,耿信笃.反相液相色谱中lgI对极性小分子溶质色谱行为的表征[J].色谱,2002,(4).
[7]Barry,Eugene F.Columns for Gas Chromatography:Performance and Selection[M].Chichester:Wiley,2007.
[8]Poole,CF,Poole,SK.Foundations of Retention in Partition Chromatography[J].Journal of Chromatography.2009,(10).
[9]刘典文.基于灰色关联的农村公共服务综合评价研究——福建省的经验性解释[J].科学决策,2010,(1).
[10]侯红卫,李雪峰.基于行为金融理论的投资者行为研究方法现状与展望[J].科学决策,2010,(2).
