基于数字预失真技术的功放性能改善研究

张福洪，黄 勇，吴铭宇

(杭州电子科技大学通信工程学院，浙江杭州310018)

0 引言

功率放大器是通信系统中的一个关键部件，功放的非线性特性引起的频谱扩张会对邻道信号产生干扰，并且带内失真也会增加误码率［1］。随着新业务的发展，现代无线通信系统中广泛采用了正交幅度调制(Quadrature Amplitude Modulation，QAM)、正交频分复用技术等高频谱利用率的调制方式。这些调制方式对发射机中射频功放的线性度提出了很高的要求。因此为了保障通信系统的功率效率和性能，必须有效的补偿放大器的非线性失真，使放大器能够高效的线性工作。目前关于功放线性化的方法有许多，如功率回退法、射频反馈技术、前馈法、LINC法、数字预失真法等，以上各种线性化技术都有其优缺点，其中数字预失真技术最大的优点就是稳定可靠、精度较高，适应能力强。因此，目前数字预失真技术被认为是最有应用前景的线性化技术。

1 数字预失真的基本原理

数字预失真技术是补偿功率放大器非线性失真最有效的方法之一，即在功放前加一个与功放非线性特性互逆的非线性模块用做预失真器以抵消补偿功放的非线性，理想情况下所加的预失真器失真将完全抵消补偿后续放大器的非线性失真，整个系统最终将是线性的［2］。

1.1 功率放大器模型

由于不同的功放有着不同的特性，没有一个通用的模型能够准确的描述各种功放特性，因此在分析功放特性的时候，首先需要给功放建立一个合适的模型，根据功放是否有记忆效应，可以将功放模型分为有记忆模型和无记忆模型［3］。本文主要针对有记忆功放模型做数字预失真研究。

在非线性系统中，经常采用Wiener模型、Hammerstein模型、Volterra级数模型建模记忆性非线性系统，其中Wiener模型和Hammerstein模型参数最少而且最容易通过数字器件来实现，但是准确有效的识别出模型参数依然是非常艰巨的任务［4］。本文采用Wiener模型作为功放的模型来设计数字预失真器，其结构组成如图1所示。

图1 Wiener模型框图

图1 中LTI模块表示线性时变系统，NL模块为非线性系统，综合两个子系统可得:

式中，al为线性系统抽头的系数，bk为奇数阶非线性系统的系数，K表示功放模型的记忆深度，L表示功放模型多项式的阶数［5］。对于有记忆非线性功放模型，数字预失真器也应该有记忆效应，因此本文的预失真器采用记忆多项式模型，有记忆多项式的模型如:

式中，Q为记忆深度，K功放模型多项式阶数。

1.2 数字预失真的结构

功放预失真估计常常采用的结构有直接学习结构、间接学习结构以及直接和间接学习混合结构。如果直接对预失真的参数进行自适应递归估计，则需要首先求得功放的模型，因此为了避免求得功放模型，采用如图2所示的间接学习结构预失真器，图中功放线性放大倍数为G，功放输出y(n)经G倍衰减后输入到预失真器训练网络，实际预失真模块为训练网络模块参数的复制，在理想情况下，期望y(n)=G·x(n)，这需要z(n)=z()，即e(n)=0，估计算法目标就是计算系数估计模块参数，传递给预失真模块。实际系统中当误差能量‖e(n)‖达到最小时，估计算法收敛，即可得系数估计模块的参数。

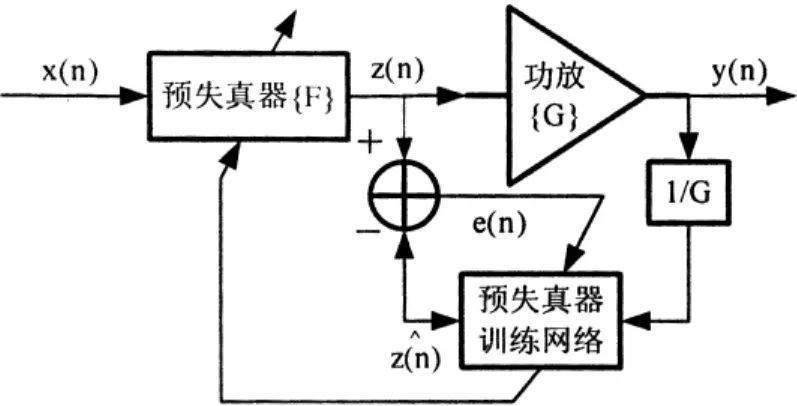
图2 间接学习结构预失真框图

式4两边都是相同阶的线性系统，采用最小均方算法(Least mean square，LMS)等算法即可算出多项式系数akq。

1.3 自适应算法设计

自适应算法是预失真系统的关键技术，常用的算法有LMS和递推最小二乘算法等，各种算法有着各自的优缺点，考虑到实际应用过程中，LMS算法不需要进行除法运算，结构简单，运算量小，因此这里选择LMS算法作为预失真系数更新算法。

系数更新:W(n+1)=W(n)+2uY(n)e*(n)。)为第 n+1 次迭代时的多项式系数，u为自适应算法的步长，其可以控制算法的收敛速度和精度。这样更新后的系数再复制给预失真器，由预失真器完成对输入信号的预失真处理。

2 系统仿真与分析

为了验证所建立的预失真算法的有效性，利用MATLAB搭建一个数字预失真系统的仿真平台。信号源采用64QAM信号，经过升余弦成形滤波然后输入到多项式查找表自适应预失真系统中进行仿真验证，自适应算法利用LMS算法，步长为0.35，预失真器模型采用具有5阶非线性，3阶记忆深度的记忆多项式，对于仿真的功放模型，采用5阶非线性，2阶记忆效应的Wiener模型，如:

式中，b1=1.010 8+j0.085 8，b3=0.087 9 －j0.158 3，b5= －1.099 2 －j0.889 1。

理想的64QAM信号的星座图如图3所示，未经过预失真器功放的输出星座图如图4所示，从图4中可以看出功放的非线性加剧了输出信号的畸变，经过组合预失真算法的功放输出星座图如图5所示，输出信号在幅度和相位上得到了很好的校正，无预失真功放输出信号的EVM为77.56%，有预失真功放输出信号的EVM为2.26%，满足系统要求，经过预失真后完全能够正确的解调。系统在各处的功率谱如图6所示，其中a表示原始输入信号的功率谱，b为信号通过数字预失真后功放的输出功率谱，c为只经过功放后输出的功率谱，明显可以看出，无预失真的功放效果很差，功率谱带外扩散严重，采用记忆多项式预失真技术的功放输出信号很好的抑制了带外频谱扩散。相比于未加预失真的输出，预失真明显降低了信号功率谱的旁瓣(约20dB)，对功放的非线性补偿效果明显。

图3 原始信号星座图

图5 经预失真+功放后信号星座图

图6 功率谱密度图

3 结束语

仿真结果表明算法能够很好的补偿功放的非线性，实现功放的线性化，该预失真器也可以用于宽带码分多址等其他宽带系统中功放的预失真。由于目前对于预失真的研究大多都基于无记忆模型，但是实际应用的多载波信号属于宽带系统，功放记忆效应明显，因此本文采用的记忆功放模型，相比于无记忆模型能够更好的模拟实际的功放特性，能够更好的验证功线性度提升的潜力和数字预失真算法的有效性。

［1］ 艾渤，李波，钟章队，等.宽带功率放大器预失真原理［M］.北京:科学出版社，2011:5－8.

［2］ 甘露.宽带射频功率放大器的数字预失真技术研究［D］.成都:电子科技大学，2009:24－32.

［3］ 黄磊，王家礼.一种改善射频功率放大器非线性的预失真方法［J］.现代电子技术，2002，21(5):45－48.

［4］ 贺彬，陈豪.基于LMS算法的自适应数字预失真技术研究［J］.空间电子技术，2010，15(2):41－44.

［5］ Ding Lei.A Robust Digital Baseband Predistorter Constructed Using Memory Polynomials［J］.IEEE Transactions on Communications，2004，52(1):150 －165.