基于五维混沌系统的数字图像加密算法
2011-09-04王晓飞王光义
王晓飞,王光义
(杭州电子科技大学电子信息学院,浙江杭州310018)
0 引言
随着以计算机和网络通信技术为代表的信息技术的不断发展和飞速普及,信息安全已经成为阻碍经济持续稳定发展和威胁国家安全的一个重要问题,对信息进行加密是用来保证信息安全的一种必要手段[1,2]。近年来的研究表明,利用混沌信号可以构造出优良的加密系统。但是以往的混沌加密技术大都基于低维混沌系统,而低维混沌加密系统存在参数和变量少,密钥空间小,抗破译能力差,安全性不高的缺点。进几年,不断有研究学者提出来新的五维混沌系统,基于五维混沌系统的图像加密算法,目前还比较少,文献3中提出来一种行列置乱和象素加密的五维超混沌系统加密算法。而本文采用全局置乱和分块象素加密的方法,具有更高的算法复杂度,实验表明该算法具有良好的加密效果,密钥空间大,抗攻击力强,加密图像象素值分布随机,具有较高的安全性。
1 五维混沌系统
文献4提出了五维混沌系统:

当 k1= -1,当 k2= -2 时系统的 Lyapunov指数分别为 λ1=1.276 95,λ2=0,λ3= -0.984 16,λ4=-2.596 86,λ5=-19.697 8,式1有一个正的Lyapunov指数,因此该五维系统是一个混沌系统。
2 加密算法设计
假设原始图像大小为M×N,设计如下加密算法,由置乱和替代两个阶段完成。
2.1 置乱算法设计
(1)产生混沌序列。给定五维混映射的初值,迭代时间步长,采用四阶五阶Runge-Kutta算法解式1得到5个长度为M×N的混沌序列X(i)。
(2)从上述五维混沌序列中选取其中的一维混沌序列X(i),将X(i)按照从大到小的顺序排列成有序列E(i),由于混沌序列的无周期性,可知X(i)中的任一元素Xi与E(i)中唯一的元素Ei对应,可以用另一索引矩阵H(i)记录Ei在X(i)序列中的位置i,如图1所示。

图1 索引矩阵生成示意图
(3)将原始二维明文图像转化成一维。可按照典型的二维行程编码排列方式将原始明文二维图像转化成为一维数组N1。
(4)对照索引矩阵H(i)和下式将N1中的元素映射到一维矩阵N2中,完成对一维数组N1的置乱。

(5)按照步骤2的逆过程,将N2由一维转化成二维,生成新的置乱后的图像I。
2.2 替代算法设计
(1)在另外4个长度为M×N的混沌序列分别取出长度为(M×N)/4的Y(i),Z(i),U(i),V(i)序列,其中 i=1,2,3,…,(M ×N)/4。取 Y(i),Z(i),U(i),V(i)序列中的每个元素进行变换如:
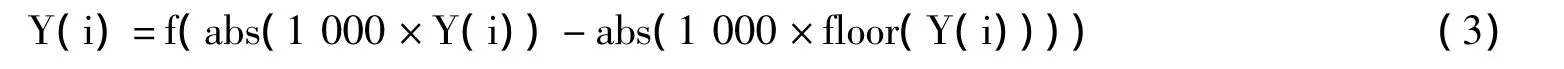
式中,f()表示向0取整,abs()表示求绝对值,mod()表示求余数,新生成的矩阵Y(i)即为加密序列。
可以取出序列中每个元素小数点后的3位数字组成整数。将该整数与256的余数覆盖原来序列中该位置的数据如:

至此上述四个序列中的元素值都介于[0,255]之间。
(2)按照置乱算法中步骤2的逆过程,将得到的新的Y(i),Z(i),U(i),V(i)序列转化成二维的矩阵 Y,Z,U,V。
(3)将置乱后的图像 I平均划分成4块I1,I2,I3,I4,如图2所示:
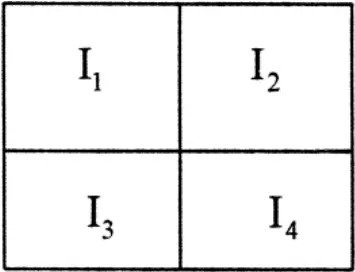
图2 置乱后图像I的分割方法
(4)将I1,I2,I3,I4中的元素值与Y,Z,U,V中相同位置元素进行异或运算,对象素值进行替代加密如:

式中,I'(x,y)表示加密后的密文象素值,I(x,y)表示置乱后第一块区域象素值,⊕表示异或运算。
(5)将进行异或得到的图像重新拼接成完整的密文图像,至此完成加密的全过程。
图像的解密算法是加密算法的逆过程,在确定系统初值和积分步长后,按照加密算法的逆过程即可解密,在此不再详述。
3 算法仿真实验
利用Matlab7.0平台,图像大小为256×256,灰度级L=256的Lena图像进行实验(M=256,N=256),取五维混沌系统的初值分别为 x0=0.835 462,y0=1.752 356,z0=0.643 875,u0=0.957 612,v0=0.417 893,积分步长为0.001,采用四阶五阶Runge-Kutta算法解微分式1,按照加密步骤进行加密,结果如图3所示。
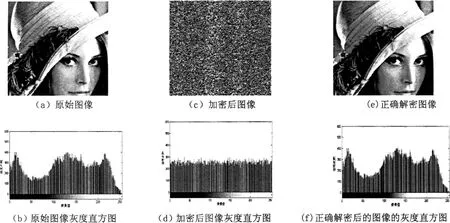
图3 加解密前后对比
由图3(c)、(e)可知,加密后的图像完全看不出原始明文图像的轮廓,而正确解密的图像与明文图像没有差别,由此可知图像的加解密效果良好。由图3(b)、(d)加密前明文图像的象素值分布数目不均匀,而加密后密文的象素值均匀分布在[0,255]范围内,所以明文的统计特性扩散到了密文的均匀分布中,大大降低了明文象素值之间的相关性,能够良好的抵抗统计分析。
4 密钥敏感性测试
本文提出的解密方案对初始参数的敏感性,以及这些参数可以用来作为密钥的假设,都得到了验证,如图4所示:
图4(a)是将解密方案中的五维混沌系统初值x0=0.835 462改为x0=0.835 462 000 001,而其余参数均保持不变的情况下得到的解密图像,图4(b)是其对应的灰度直方图。
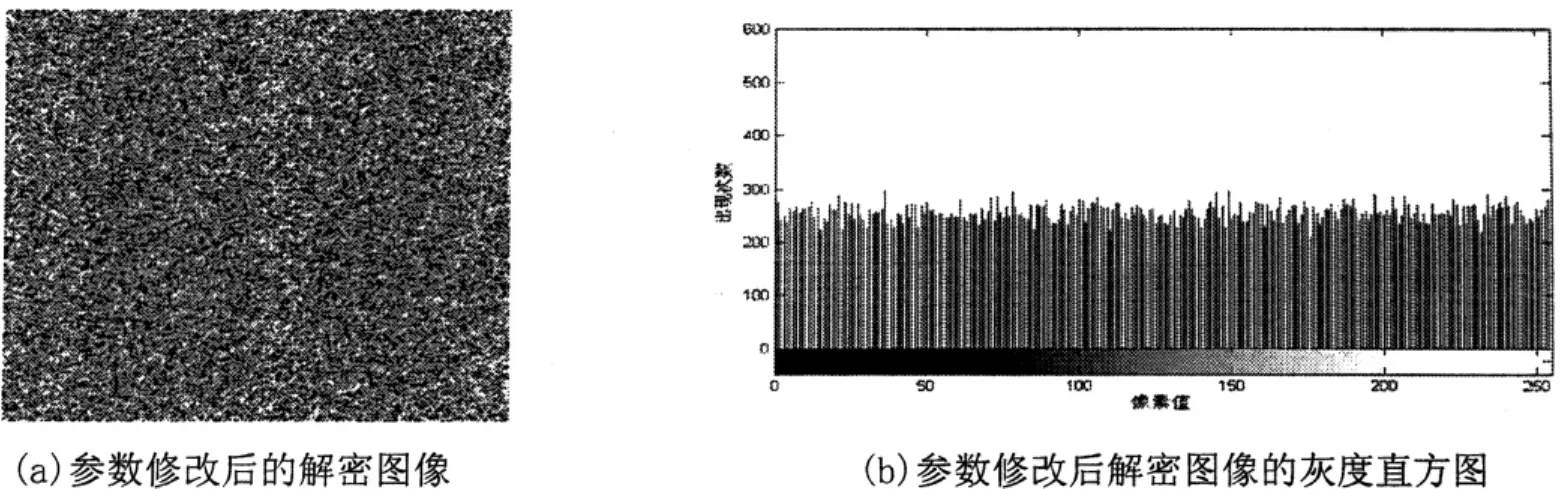
图4 密钥敏感性测试
5 结束语
本文提出来一种新的基于五维混沌系统序列的图像加密算法,该算法中的图像全局置乱和分块加密均基于五维混沌系统。仿真实验和分析表明,该算法密钥空间大,抗攻击力强,密文图像象素值分布随机,可以有效的抵御统计分析攻击,具有较高的安全性。
[1] Cheng Howard,Li Xiaobo.Patial encryption of compressed images and vides[J].IEEE Transcations on Signal Processing,2000,48(8):2 439 -2 551.
[2] Dang P P,Chan P M.Image encryption for secure Internet multimedia applications[J].IEEE Transcations on Consumer E-lectronics,2000,46(3):395 -403.
[3] 王玉惠,陈哨东.基于五维超混沌系统的全球信息栅格图像加密算法[J].吉林大学学报,2010,29(1):51-56.
[4] 韩峰,唐驾时.一个五维受控混沌系统的动力学行为[J].动力学与控制学报,2010,8(3):205-209.
[5] 李鹏,田东平.基于超混沌序列的数字图像加密算法[J].微电子学与计算机,2008,25(3):4-7.
