桥梁平转施工称重试验及启动牵引力计算探讨

2011-09-04陈顺超黄平明王吉磊

铁道建筑 2011年11期

陈顺超，黄平明，王吉磊

(1.长安大学桥梁与隧道陕西省重点实验室，西安 710064;

2.西南林业大学土木工程学院，昆明 650224;3.中铁十局济铁公司，济南 250001)

当新建桥梁跨越交通繁忙的既有铁路或高速公路时，为了最大限度地减小桥梁施工对交通运营的影响，首选方案就是平面转体施工。平面转体施工的关键部位是转体系统，它由上转盘、下转盘及牵引系统组成。目前的桥梁转体施工，转盘结构普遍采用凹形预制钢球铰，外加钢管混凝土撑脚作为保险支腿;牵引系统普遍采用预埋钢铰线索、牵引反力座及电脑控制同步连续千斤顶［1-4］。

桥梁转体要想顺利、安全、平稳，就必须保证梁体在转动过程中始终处于平稳状态，并且牵引系统能提供充足、稳定的牵引力。要做到这两点，必须通过称重试验测试转动体的不平衡力矩以及静摩阻系数，从而制定相应的配重方案，并根据实际支承情况计算启动牵引力，确保牵引系统的动力安全系数满足要求。目前，称重试验虽已在转动体不平衡状况识别中普遍采用，《公路桥涵施工技术规范》(JTJ 041—2000)也提供了启动牵引力的计算公式，但仍然存在不完善之处。本文将结合滨州—德州高速公路上跨京沪铁路立交桥转体施工监控实践，对转体桥称重试验及启动牵引力计算进行探讨。

1 转体称重试验的讨论

转体称重试验的目的是测试转动体的不平衡力矩、静摩阻力矩及静摩阻系数，并据此制定相应的不平衡配重方案。绝大多数情况，球铰的摩阻力矩大于不平衡力矩，砂箱拆除后，撑脚并不落地，转动体处于球铰单独支承状态。

称重试验的原理是假设转动体能绕球铰发生刚体转动，当转动体发生转动位移突变时，转动体在施加的转动力矩、不平衡力矩及静摩阻力矩三者作用下刚好处于力矩平衡的临界状态。目前通常的做法如图1所示，分别在转动体的两个相对方向施加竖向顶升力，并同时测试梁体的竖向位移，绘制位移—力曲线，从中判断出拐点，拐点所对应的力即为临界力 P1，P2，顶升力作用点至球铰中心距离分别为 L1，L2，根据下述公式(1)～公式(3)即可计算得到不平衡力矩、静摩阻力矩及静摩阻系数。

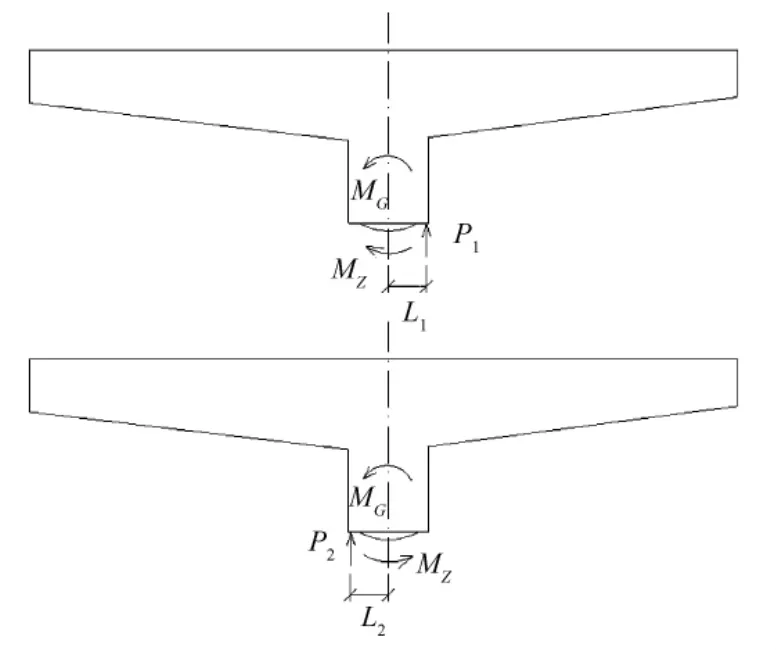
图1 称重试验常规做法原理示意

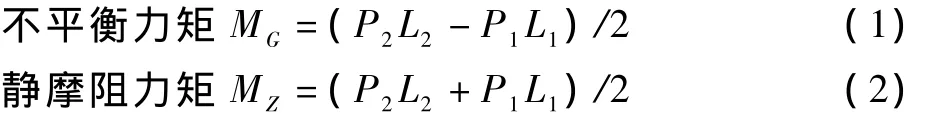
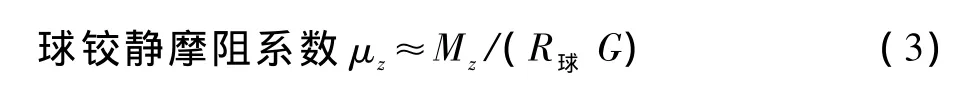
其中，R球为球铰球面半径;G为转动体总重量。

从上述分析可见，称重试验的关键是如何较准确地确定转动体由静止到转动的临界点，这又涉及到力和位移两个方面的因素，下面分别来分析。

1.1 作用力的影响

称重试验最理想的方式是直接施加转动力矩，但实际只可能通过力的施加来产生力矩。当力作用于刚体时，其作用效应可分为转动力矩和力两部分，其中转动力矩属于有效部分。为了润滑，上、下球铰之间充填有一定厚度的黄油四氟粉，如图2所示。当有顶升力作用时，同侧的黄油压力会减小，空隙变大，相对一侧的黄油会被压迫、挤出，空隙减小。并且顶升力越大，此效应越显著。可见，竖向力的作用对球铰的均匀转动是不利因素，在保证转动力矩的情况下，力越小，越接近球面转动的理想状态。所以，从提高测试精度的角度考虑，作用力的力臂越长越好。

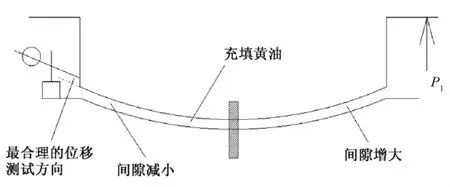
图2 竖向力对球铰影响的示意

作用力的施加位置位于悬臂端部是最理想的状况，这存在两种可能。一是在梁端的下部用小型千斤顶顶升，这种方式实际不可行。因为梁下需要搭设支架才能有着力点，支架的稳定性成问题，而且梁端下部顶升将使悬臂根部断面的底板受拉，有可能损坏梁体。二是在梁端上部压重，在悬臂根部产生的负弯矩刚好由顶板的预应力钢束承担。以滨德高速为例，转体T构长76 m，要克服不平衡力矩 +摩阻力矩，偏安全地考虑需要在距梁端2 m处压重450 kN。则上缘最大拉应力、下缘最大压应力增量分别约为0.7 MPa，0.82 MPa，且压重完成后所有截面均为压应力，足够安全。压重横向位置只要不集中于顶板中央，对箱梁局部也不会造成损坏。

梁端压重的加载方式，由于竖向力小，其试验精度显然优于常用的墩底顶升的方案，安全性也能保证，唯一的缺点是吊装工作量较大。现场吊装条件允许时，可优先考虑采用。

1.2 位移测试

目前，称重试验通常测试球铰的竖向位移，其实并不合理。由于竖向力的影响，竖向位移并非完全由球铰的转动引起，实际上前期位移主要是黄油层受压或减压所导致的竖向位移。位移大小与黄油层的厚度有关，且位移与力之间也并非呈线性关系。反映在位移—力曲线上表现为曲线微凸，拐点不明显，难以判断。从称重试验的原理来看，既然是球面转动，则应该是测试沿球铰边缘切线方向的位移最为合理，如图2所示。当然安置百分表时，如果沿切线方向安置，容易造成接触点打滑，影响测试结果。但是由于切线的水平夹角较小，通过测试水平位移，也能消除黄油层竖向位移的不利影响，起到与测试斜向位移同样的效果。

为了探究竖向位移与水平位移的不同，在滨德高速公路上跨京沪铁路立交桥转体称重试验中对两者进行了对比研究。图3为同一次试验对应的位移—力曲线图。由图3中竖向位移曲线可知，突变前竖向已产生较大位移，实际反映了黄油层的影响;而图3中水平位移曲线在球铰转动之前几乎没有位移，且突变更明显。竖向位移—力曲线在突变前微凸，表现为非线性的性质，可以想象黄油层越厚，非线性将越明显;而水平位移则受黄油层的影响很小，拐点更容易判断。由图3中竖向位移曲线可得临界力为3 326 kN，由图3中水平位移曲线可得临界力为3 342 kN，采用时应以后者为准。

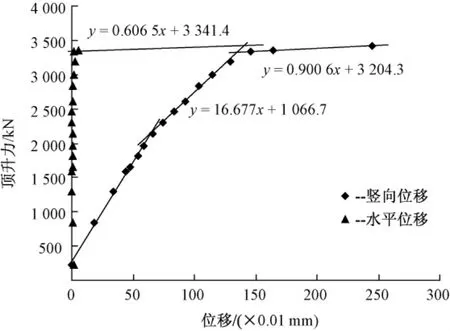
图3 位移—力曲线

由上述分析可见，测试水平位移能消除黄油层的不利影响，较测试竖向位移更为合理。实际测试时，应以水平位移测试为准，或两者同时测试，综合分析。

2 启动牵引力的计算

根据《公路桥涵施工技术规范》(JTJ 041—2000)，转体牵引力的计算公式为［5］

式中，T为牵引力;G为转体总重量;R为下球铰平面半径;D为牵引力偶臂;f为静摩阻系数，可由称重试验得到。

公式(4)推导的前提是整个转体重量由球铰单独承担。不考虑中间转轴的影响，支承面可简化为圆形，圆可看成由无数个圆心角无限小的等腰三角形组成，而三角形的重心位于垂线的2/3处，则容易得到公式(4)。

目前的转体系统普遍采用球铰+撑脚保险腿的形式，转体时最理想的状况是球铰单独支承，而撑脚与滑道处于若即若离的状态，仅起保险的作用。实际上，这种理想状况是不可能存在的，因为撑脚下要放入四氟滑片，挤入黄油，实际已经受力。而且为了防止平转时转体竖向“大翻身”，普遍采用的是不平衡配重方案。为了保险，还在翘起的一侧施加顶升力，使撑脚产生一定的压力。因为撑脚摩阻力的力臂更大，此时如仍然按公式(4)计算启动牵引力，则显然会偏小。所以，比较合理的计算方法，应该考虑撑脚参与受力的实际情况。撑脚参与受力后，转动体实际处于超静定结构状态，要精确考虑撑脚的受力状态是不可能的，也没有必要。转前配重完成后，对翘起一侧继续顶升，这时转动体实际已出现转动位移突变，由于撑脚和球铰下黄油的蠕变，其最终趋势是趋向于球铰和一侧的撑脚共同承载。所以，承载的面积可考虑为球铰全部面积加上半数撑脚的面积，如大部分设计是6个撑脚，即可考虑3个撑脚参与受力。

撑脚底板的形状为扇形，如图4所示。设撑脚摩阻力合力为F，合力臂为R撑脚，撑脚内外侧平面半径分别为 R1、R2，摩阻系数为 f，撑脚底压应力为 σ，扇形所对应圆心角为φ，则有

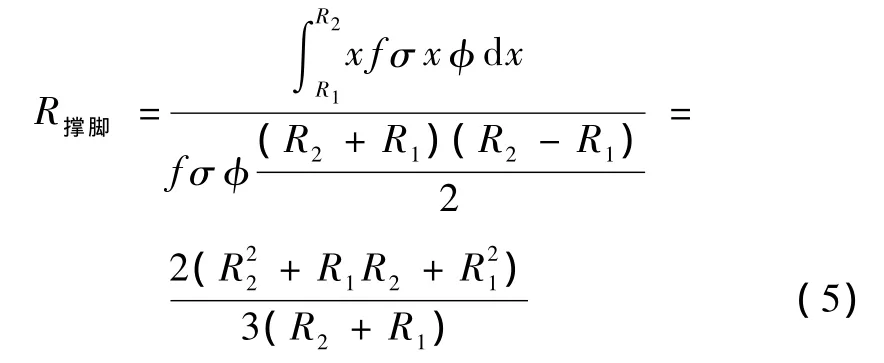
则转体牵引力的计算公式为

图4 撑脚摩阻力臂计算示意

滨德高速公路上跨京沪铁路立交桥转体系统采用环道与中心支承相结合的球铰转动体系，单幅转体质量约4 500 t;下球铰平面直径3.0 m，上球铰平面直径3.7 m，中心转轴直径0.26 m，球铰球面半径6.02 m，转台直径6.60 m;撑脚内、外侧半径分别为2.45 m，3.25 m，六个撑脚对称布置于纵轴线两侧，每组撑脚由2个直径600 mm的钢管混凝土圆柱状结构组成，撑脚下钢板面积为1.16 m2;实测静摩阻系数为0.041。转前对转动体进行了顶升，使得撑脚接触滑道，根据顶升情况考虑3个撑脚参与受力。实测启动牵引力为467 kN，式(4)和式(6)计算结果分别为274 kN和444 kN。按规范公式(4)计算的启动牵引力比实测值偏小很多，而按简化公式(6)的计算值与实测值则较吻合。因此，应考虑撑脚参与受力的实际情况，按公式(6)计算启动牵引力，具体参与的程度应视撑脚接触的情况具体考虑，一般可考虑为半数撑脚参与受力。