IR-UWB穿墙测距误差研究

蒙 静，张钦宇，张乃通，，张霆廷，马 琳

(1.哈尔滨工业大学 深圳研究生院，518055深圳，starsmeng@126.com;2.哈尔滨工业大学电子与信息工程学院，150001哈尔滨)

基于脉冲超宽带(Impulse Radio Ultra-wideband，IR-UWB)的无线定位系统充分利用了IRUWB信号高达纳秒级别的时间分辨率，结合到达时间(Time-of-Arrival，TOA)的测距理论上可获得厘米级别的定位精度[1].然而，无线定位测距性能也受到IR-UWB信号传播特性的影响，特别是复杂室内环境下的非视距(Non-Line-of-Sight，NLOS)传播是造成TOA测距误差的主要原因.由于IR-UWB信号具有强穿透能力，是目前众多短距离定位技术无法匹敌的[2]，深入研究IR-UWB信号穿墙透射机理及其导致的NLOS测距误差，对无线定位系统设计和性能优化都具有重要意义.

目前在视距(Line-of-Sight，LOS)环境下对IR-UWB定位系统测距误差的研究已经获得了较统一的高斯分布模型[3－4]，而对 NLOS误差的研究一直没有定论，主要是由于室内环境统计相似性已明显消失[5]，有限环境测量结果通用性不大.特别是IR-UWB穿墙传播中的距离误差不仅与收发节点距离和障碍物参数有关，也受到脉冲信号传播特性影响.结合IR-UWB信号穿墙传播特性对测距误差的研究很少，多是单独研究IRUWB信号的透射机理，如文献[6－7]对不同天线和墙体对IR-UWB信号传播的影响进行了实测，文献[8]将传统透射系数的时域表达式用于IR-UWB信号透射的建模，但并未给出相应仿真结果.且上述文献中均未考虑IR-UWB信号传播过程中的频率依赖性.基于此，本文将IR-UWB信号穿墙传播特性与TOA测距误差研究相结合，将NLOS距离误差建模为由脉冲信号在墙体内额外传播时延导致的几何距离误差和脉冲波形畸变导致的峰值偏移误差.并推导了几何距离误差限，通过对IR-UWB信号穿墙透射传播机理的建模，定量分析了脉冲信号波形失真问题，以及不同墙体结构导致的相关峰值偏移误差对完全NLOS环境下TOA距离估计的影响.

1 IR-UWB穿墙测距误差

NLOS传播环境下，IR-UWB信号具有的强穿透障碍物能力使得DP能够穿墙传播到达接收机.然而，由于电波信号在障碍物内的传播速度小于自由空间传播速度，IR-UWB信号穿墙传播引入的额外传播时延必然产生TOA测距误差[9].同时，IR-UWB信号的频率依赖性使其在传播过程中发生波形畸变[10]，脉冲峰值位置不确定，也会导致相干TOA测距误差.从而使得最终的TOA距离估计结果恒大于收发节点间实际距离.因此，IR-UWB穿墙测距误差由2部分组成:

1)电波在收发节点间折射后实际传播路径与直线距离的几何距离误差εgeo;

2)IR-UWB信号波形失真导致相关峰值位置不确定产生的峰值偏移误差εpeak.

此处需要明确的是，本文暂不考虑多径传播对相干TOA估计的影响，即只关注仅有穿墙透射信号达到接收机的情况.

2 几何距离误差理论限

考虑二维平面的距离误差推导，实际三维空间的距离误差可看作是二维平面的扩展.将收发节点置于如图1所示的参考坐标轴中.设收发节点均为全向天线，增益为1.图中目标节点A和参考节点B的坐标分别为(xA，yA)和(xB，yB)，则AB节点间的直线距离为

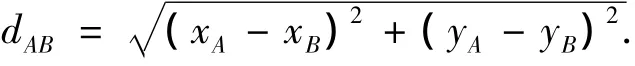
根据等效源法，从A点以入射角θi入射到墙体表面后穿墙传播到B点的信号，可等效为从A'点以相同入射角穿墙传播到B点，信号的传播路径等效为A'到B的直线路径.则节点A'和B之间的直线距离为 dA'B= Δy/sin θi.其中 Δy=|yA－ yB|.接下来计算IR信号在墙体内的额外传播时延.设墙体厚度为dwall，脉冲信号在墙内的等效传播距离为d'=dwall/cos θi.墙体内传播的额外时延为

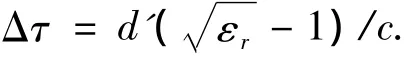
其中εr为墙体的相对介电常数，c为光速.对应的额外距离为

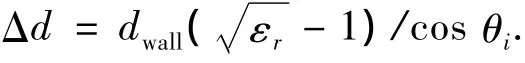
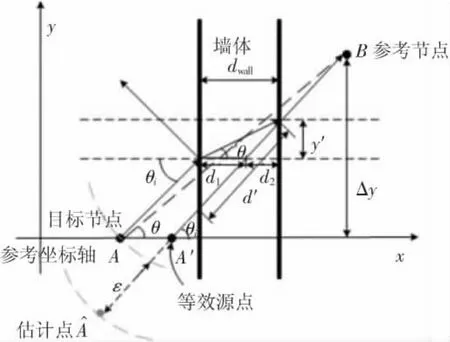
图1 完全NLOS传播几何误差

因此，TOA距离估计误差为

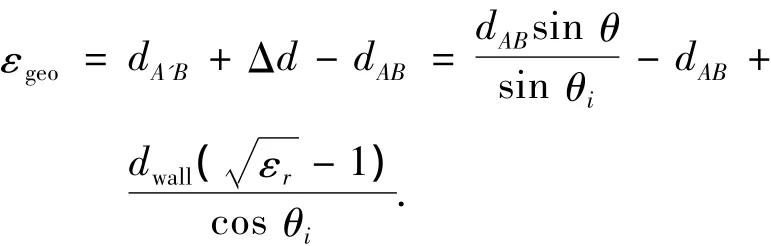
上式可进一步写为

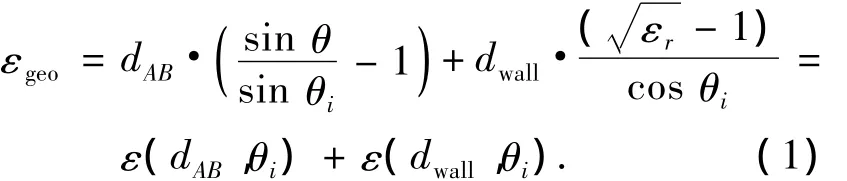
其中θ为AA'与AB的夹角.由此可见，IR-UWB信号穿墙传播过程中的几何距离误差，由收发节点间距离、墙体参数以及入射角共同决定.此时通过相干TOA估计可能使得目标节点A的位置偏移到以接收节点B为圆心，估计节点Â到B的直线距离为半径的圆上.

由式(1)，入射角和收发节点间距离变化对IR-UWB信号穿墙测距误差的影响见图2.设墙体为混凝土墙和石膏板，UWB频段上对应的相对介电常数和电导率均值分别为混凝土εr=6.05，σ=0.001 95 s/m;石 膏 板 εr= 2.8，σ =0.03 s/m.墙体厚度均为15 cm，收发节点间直线距离2 m.图2(a)中εgeo与ε(dwall，θi)变化趋势相同，随着入射角的增加而增加，与收发节点间距离有关的误差项ε(dAB，θi)为负数，也随着入射角的增加而增加.单从数值大小上，ε(dwall，θi)远大于ε(dAB，θi).当入射角 θi≥ π/3 后，εgeo基本与ε(dwall，θi)重合.图2(b)中固定混凝土墙厚度为15 cm，入射角θi= π/4时，ε(dwall，θi)为常数，dAB的变化对总的距离误差基本无影响.因此，式(1)中等式右边第二项，即与墙体参数有关的距离误差项决定了IR-UWB信号穿墙TOA测距的主要误差.

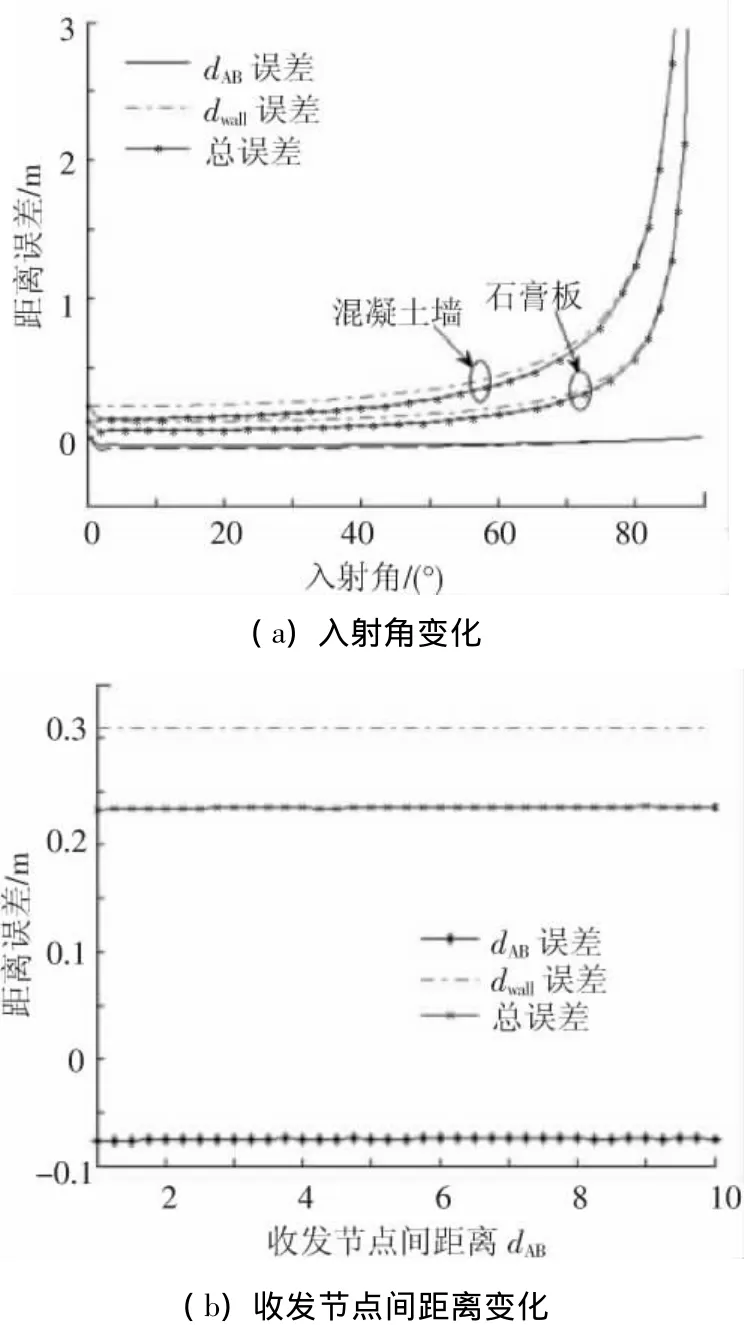
图2 IR-UWB穿墙测距几何距离误差限

3 IR-UWB穿墙透射波形失真

IR-UWB信号穿墙传播导致的峰值偏移误差εpeak完全由IR-UWB信号穿墙透射波形决定，明确波形失真对相干TOA测距误差的影响，必须对IR-UWB单径信号穿墙传播建模.

3.1 穿墙透射模型

考虑IR-UWB信号穿透单个厚度为d的均匀墙体的情况.IR-UWB信号入射到不同介质的分界面会同时发生反射和折射，穿墙传播更为实际的情况是电磁波会在墙体内的分界面之间发生连续多次反射[11]，如图3 所示.图中Rij和τij分别为电磁波在区域i和区域j分界面的反射和折射系数.因此总的透射信号是首条透射径与多个连续反射－透射径的叠加.根据图3的几何关系，IRUWB信号在墙体内单次传播的衰减为Pd=e－jkl.其中k= ω为电磁波在墙体内的传播常数，l=d/cos θt为实际传播距离.图中 R12= Γ⊥，‖为垂直极化和水平极化的Fresnel反射系数，τij=Rij+1，且R23=R21=－Γ.修正的透射系数可以表示为如下的级数形式:

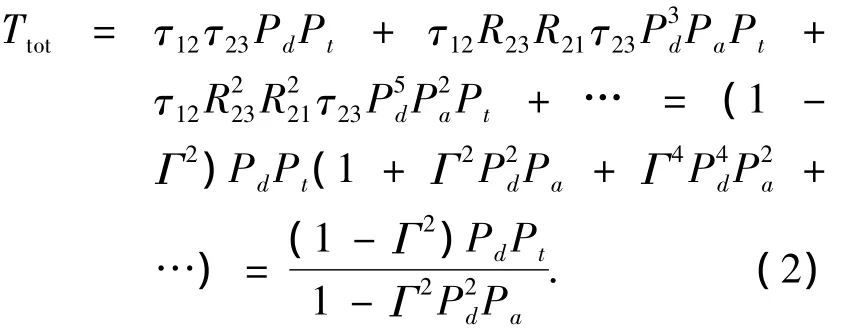
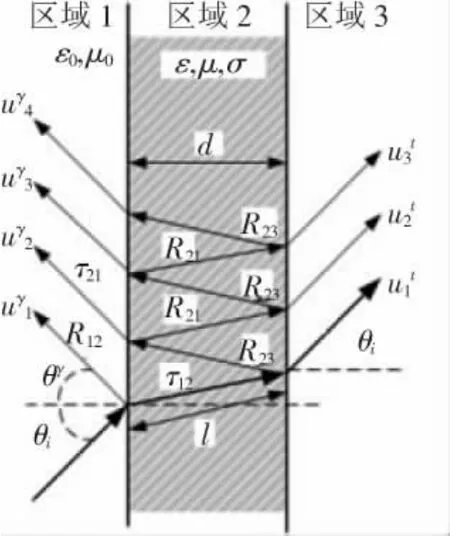
图3 IR-UWB穿墙传播模型

由式(2)可知，IR-UWB信号的穿墙传播特性与墙体参数密切相关.表征材料电磁特性的参数有3个:电容率ε，电导率σ和磁导率μ.室内材料通常都是非磁性介质，因此其相对磁导率μr近似为1.对于有损耗媒质，其等效的复介电常数可表示为，其中介电常数为为自由空间介电常数，εr为相对介电常数，ε″为介电损耗.该复介电常数直接决定了电磁波在有损耗媒质中的传播常数k.等效介电常数中已包含频率因子ω，因此通常所说的媒质介电常数是指某一特定频率上的电参数值.文献[13]对室内常见材料电参数(相对介电常数和电导率)在UWB频段的实测结果指出材料电参数是具有频率依赖性的.对IR-UWB信号穿墙传播的研究必须考虑墙体电参数随频率变化的问题.本文使用子频带的方法研究IR-UWB信号的穿墙传播[14].其整个过程可描述为

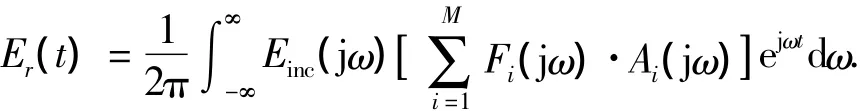
其中Er(t)为时域接收信号;Einc(jω)为发射信号Einc(t)的频谱;Fi(jω)为第i个子频带的透射系数;Ai(jω)为第i个子频带对应的矩形窗函数;M为所有子频带数目.

3.2 IR-UWB信号波形失真分析

使用如下的高斯脉冲二阶导函数作为发射脉冲:

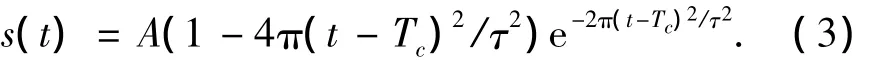
其中A为高斯二阶导脉冲的幅度，τ为脉冲成形因子，Tc为时间偏移量.仿真中 A=1 V，α=0.160 ns，Tc=0.5 ns.该脉冲对应的距离分辨率ΔR≈3.75 cm.室内环境下常见的障碍物材料及尺寸如表1所列，钢筋混凝土墙厚度为15 cm，钢筋直径分别为2 cm和4 cm，间隔7.5 cm.根据文献[13]中给出的墙体电参数，高斯二阶导脉冲信号垂直入射到不同障碍物后的透射波形如图4所示.

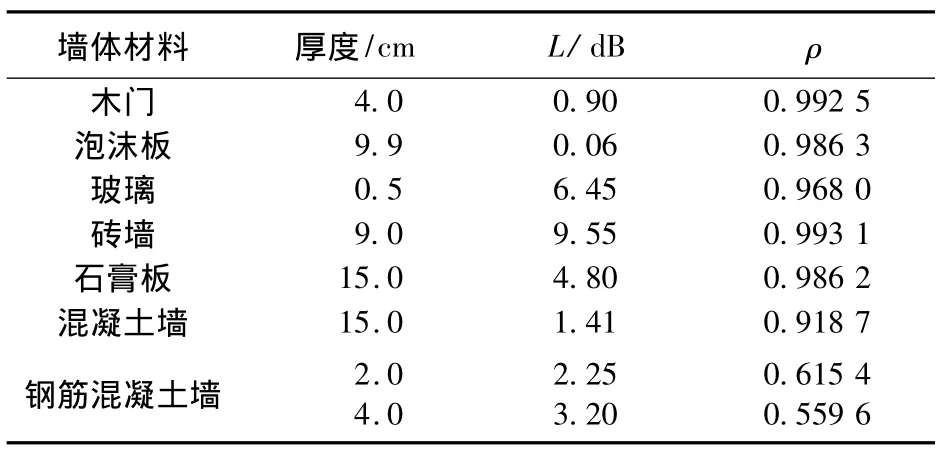
表1 室内常见障碍物尺寸及IR-UWB信号穿墙透射性能相关参数

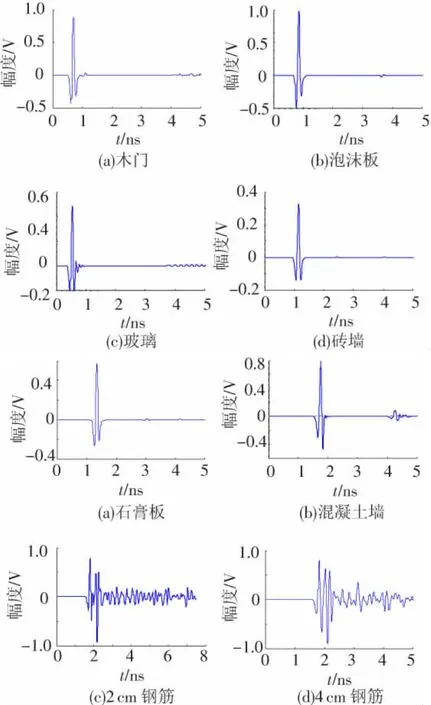
图4 IR-UWB信号穿透不同墙的透射性能相关参数

此处使用能量损耗L和波形相关度ρ衡量IR-UWB信号的波形失真，分别定义为

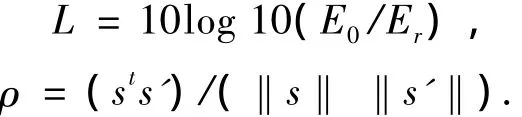
4 TOA测距误差分析

根据3.2节的仿真结果，结合相干TOA测距算法，仅有穿墙透射信号时，可将接收信号相关峰值的TOA估计作为IR-UWB信号的最优到达时间.图5为IR-UWB信号穿透15 cm石膏墙、混凝土墙和钢筋混凝土墙之后，分别使用发射脉冲和接收信号作为模板信号时的归一化自相关和互相关波形.自相关波形有明显的峰值，相对于峰值点是完全对称的，互相关波形出现了2个正负峰值.自相关和互相关峰值间的偏移量即为波形失真导致的相关峰值偏移误差.对于钢筋混凝土的情况更为复杂，互相关波形出现了2个较大的峰值.对图4中穿墙透射波形进行相关处理之后，由于波形畸变导致的相关峰值偏移TOA估计误差εpeak见表2.其中几何距离误差εgeo由式(1)直接算出.IR-UWB信号穿透均匀墙体的波形失真造成的峰值偏移误差都小于几何距离误差，其数值维持在单个脉冲信号持续时间对应的距离分辨率范围;对于非均匀的钢筋混凝土墙，峰值偏移误差已经与几何误差相当，此时几何距离误差已不能很好的描述IR-UWB信号穿墙传播导致的NLOS距离误差.

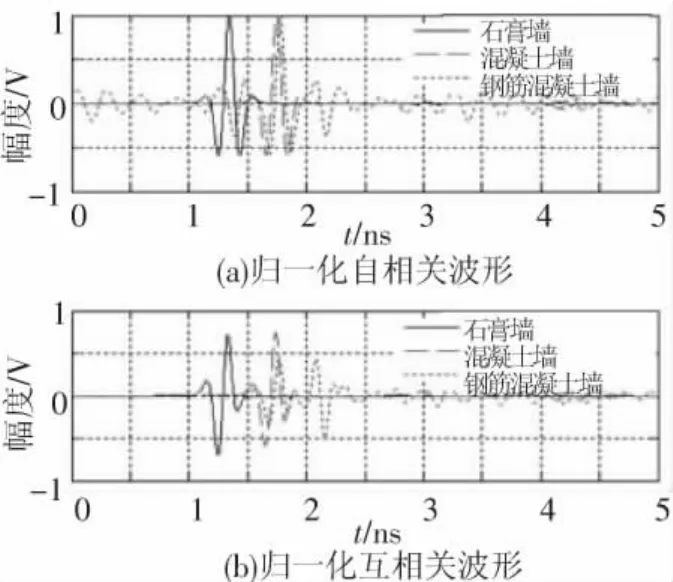
图5 IR-UWB透射信号的自相关和互相关归一化波形

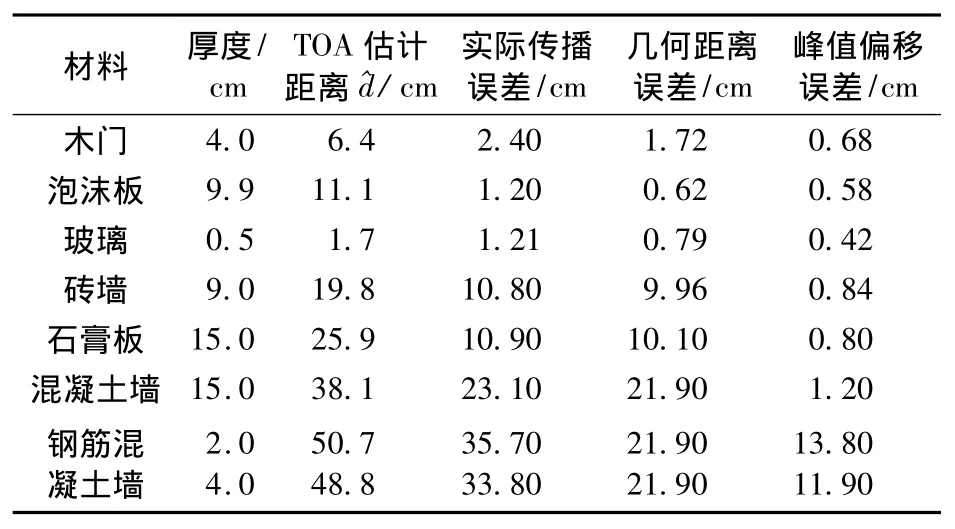
表2 不同墙体导致的距离误差比较

综上，对于完全NLOS环境下IR-UWB信号穿墙传播导致的TOA距离估计误差，本文第2节推导的几何距离误差限εgeo是该NLOS误差的主要部分，其由墙体材料和墙体内传播距离决定，收发节点间距离的影响可忽略;另一部分NLOS距离估计误差是由IR-UWB信号波形畸变导致的相关峰值偏移误差，对于均匀墙体，峰值偏移误差εpeak维持在脉冲对应的距离分辨率量级，而非均匀墙体导致的峰值距离偏差极大，文中给出的钢筋混凝土墙体结构导致的峰值偏移误差已接近几何距离误差.此时必须考虑脉冲信号畸变对测距精度的影响.

5 结论

NLOS环境下IR-UWB信号穿墙传播会导致相干TOA测距误差.本文将IR-UWB信号穿墙测距NLOS误差建模为由脉冲信号在墙体内额外传播时延导致的几何距离误差和脉冲波形畸变导致的峰值偏移误差之和.几何距离误差理论主要由IR-UWB信号在墙体障碍物内的传播距离和材料决定，收发节点间距离对其影响可忽略.IR-UWB信号穿墙传播中能量损耗随墙体电导率增加而增大;波形畸变则主要受墙体的相对介电常数和非均匀性影响.对于厚度与脉冲信号波长相当的障碍物，还必须考虑介质板内多重反射对透射波形的影响.IR-UWB信号穿透均匀墙体的波形畸变导致的峰值偏移误差小于几何距离误差，其数值维持在脉宽对应的距离分辨率量级;而对非均匀墙体来说，峰值偏移误差是NLOS误差的重要组成部分，在对IR-UWB测距误差修正中必须加以考虑.本文的后续工作拟利用该确定环境测距误差信息结合实际信道分布，完善IR-UWB穿墙测距误差修正理论，以及对NLOS定位性能的优化.

[1]GEZICI S，TIAN Z，GIANNAKIS G B，et al.Location via ultra-wideband radios:a look at positioning aspects of future sensor network[J].IEEE Signal Processing Magazine，2005，22:70 －84.

[2]PAHLAVAN K，LI X，MAKELA J P.Indoor geolocation science and technology[J].IEEE Communication Magazine，2002，40(2):112 －118.

[3]ALAVI B，ALSINDI N，PAHLAVAN K.UWB channel measurements for accurate indoor localization[C]//IEEE Military Communication Conference 2006.Piscateway:IEEE，2006:1－7.

[4]BELLUSCI G，JANSSEN G，YAN J，et al.Modeling distance and bandwidth dependency of TOA-based UWB ranging error for positioning[J].Research Letters in Communications，2009，2009:1－4.

[5]LI Qiang，ZHANG Y P.Waveform distortion and performance of impulse radio with realistic antennas in deterministic multipath channels[C]//Proceedings of IEEE Vehicular Technology Conference 2008.Piscateway:IEEE，2008:260－264.

[6]SCHEJBAL V，BEZOUSEK P，CERMAK D，et al.UWB propagation through walls[J].Radio engineering，2006，15(1):17 －24.

[7]NEMEC Z，MRKVICA J，SCHEJBAL V，et al.UWB through-wall propagation measurements[C]//First European Conference on Antennas and Propagation 2006.Nice:European Network of Excellence ACE，2006:1－6.

[8]QIU R C.A generalized time domain multipath channel and its application in ultra-wideband(UWB)wireless optimal receiver design-Part II:physics-based system analysis[J].IEEE Transactions on Wireless Communications，2004，3(6):2312 －2324.

[9]JOURDAN D，DARDARI D，WIN M Z.Position error bound for UWB localization in dense cluttered environments[J].IEEE Transactions on Aerospace and Electronic Systems，2008，44(2):613 －628.

[10]MUQAIBEL A，SAFAAI A.Characterization of wall dispersive and attenuative effects on UWB radar signals[J].Journal of the Franklin Institute Advances in Indoor Radar Imaging，2008，345(6):640 －658.

[11]BURNSIDE W D，BURGENER K W.High frequency scattering by a thin lossless dielectric slab[J].IEEE Transaction on Antennas Propagation，1983，AP －31:104 －110.

[12]HAYT W H，BUCK J A.Engineering Electromagnetics[M].Beijing:China Machine Press，2001:420－430.

[13]MUQAIBEL A，SAFAAI A，BAYRAM A，et al.Ultrawideband through-the-wall propagation[J].IEE Proceeding of Microwave and Antennas Propagation，2005，152(6):581－588.

[14]ZHAO Yan，HAO Yang，ALOMAINY A.UWB onbody radio channel modeling using ray theory and subband FDTD method[J].IEEE Transactions on Microwave Theory and Techniques，2006，54(4):1827 －1835.