钢框架结构基于变形性能的实用高等设计方法
2011-09-03张耀春邵永松赵金友
金 路,张耀春,邵永松,赵金友
(1.哈尔滨工业大学 土木工程学院,150090哈尔滨,duobeibei@163.com;2.东北林业大学土木工程学院,150040哈尔滨)
结构进行高等分析与设计在满足承载能力极限状态的同时,还应验算正常使用极限状态下的框架变形.但已有研究发现,按基于极限承载力高等分析方法设计的多高层钢框架结构,变形验算往往不符合正常使用极限状态的要求,需要增大构件截面以满足变形限值,即大多数情况正常使用极限状态对截面选择和材料用量起控制作用[1-2].另一方面,在考虑几何非线性影响时,一般按缺陷最不利分布,将规范规定的结构整体和单个构件的初始缺陷布置在引起框架变形方向的同侧,这可能导致多高层钢框架结构的柱顶侧移超过结构整体垂直度要求,也与实际缺陷呈随机分布的情况不符.
本文采用蒙特卡罗法拉丁超立方技术模拟了结构构件随机初始几何缺陷的分布与遇合,应用ANSYS程序对高层钢框架进行大量的二阶弹塑性高等分析.通过对比多种分析方法研究了初始缺陷对结构变形性能的影响,由此提出了一种基于变形性能的实用高等设计方法,为钢结构规范的修订提供参考.
1 初始几何缺陷的考虑方法
1.1 初始几何缺陷实测值
钢结构构件制作和安装误差会产生构件和结构整体的初始偏差,在施工过程中既要保证各构件和各节间的误差在容许限值内,也要控制各层累计误差不超出结构整体垂直度的要求.特别对于高层和超高层结构,需要现场实测并及时反馈到构件的制作或安装中去,以满足安装精度的要求[3].因此,实际结构的初始几何缺陷是有控而随机分布的.
以2个已竣工工程结构的垂直度偏差实测验收记录为例,图1为大连市经济开发区奥镁有限公司钢结构塔楼的单柱各层垂直度偏差,由浙江东南网架股份有限公司施工.该结构为钢框架结构,11层,建筑总高度72 m,建筑面积5 000 m2.图2为杭萧钢构股份有限公司施工的成都市大源高新区成达工程公司总部大楼单柱各层的水平向垂直度偏差.该结构形式为钢框架-支撑结构体系,地下3层,地上34层,建筑总高度138.6 m,建筑面积80 000 m2.
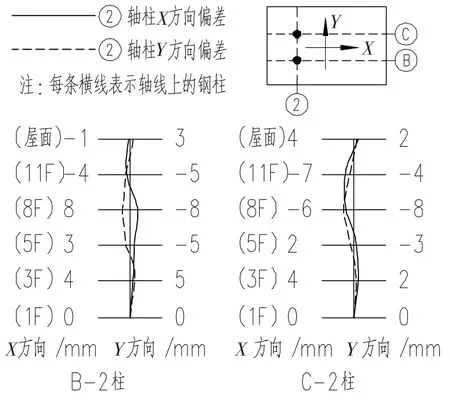
图1 钢框架结构的垂直度偏差
从上述工程验收记录看出,实测结构构件的初始缺陷大小和方向是随机分布的,结构整体垂直度偏差因各缺陷之间的随机遇合随着层数增加而逐渐减小,并非呈最不利累积分布.现有工程实测的垂直度偏差可作为相同类型结构初始缺陷量化的依据.
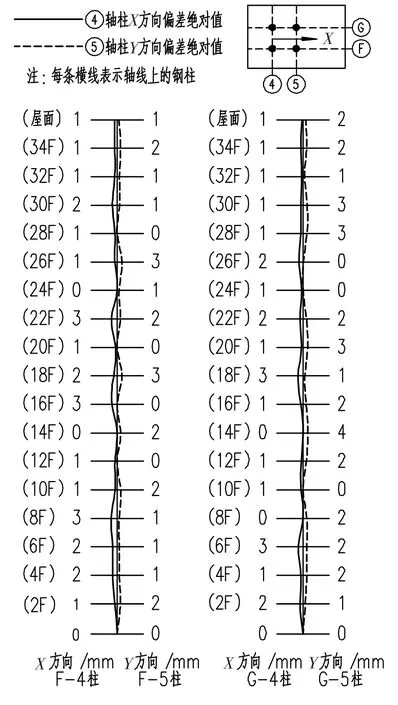
图2 框架-支撑结构的垂直度偏差
1.2 规范方法
目前,各国家和地区规范考虑初始缺陷的计算方法各不相同.美国规范AISC(2005)[4]采用直接分析法假定整体初始垂直度为层高的1/500,构件弯曲幅值为1/1 000.
欧洲规范 EC3(2003)[5]规定构件的初弯曲缺陷幅值e0/l为1/350~1/100,认为结构初始倾角φ与该层框架柱的高度h和该层柱的个数m有关,即

在英国规范 BS5950[6]和香港 HKC—2005[7]规范中,若考虑了缺陷的等效名义荷载,则不再与其他水平荷载进行组合.
我国《钢结构设计规范》[8]通过假想水平力来综合体现结构构件的初始缺陷
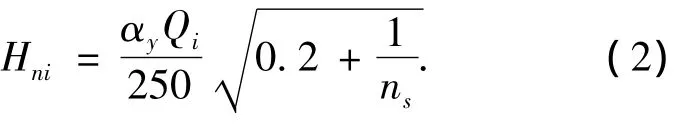
此外,也可以按中国规范 GB50205—2001[9]规定的多高层钢结构单节柱垂直度允许偏差h/1 000、柱侧曲矢高允许偏差h/1 500及梁弯曲矢高允许偏差l/1 200作为结构整体和构件的初始缺陷,h为柱高度,l为梁跨度.
按上述规范计算的结构整体和构件的初始缺陷一般保守地布置在结构变形的同一方向,夸大了初始缺陷的不利影响,可能导致多高层钢框架结构的初始累积缺陷不满足整体垂直度的要求.
1.3 蒙特卡罗法
结构各层的初始垂直度偏差及梁柱初始弯曲间的随机分布有无穷种遇合模式,很难通过理论方法考虑.而蒙特卡罗法以概率模型为基础,能通过大量数值模拟试验给出问题近似解,对于解决与随机变量有关的实际问题十分有效[10].此外,通过采用拉丁超立方抽样方法,在多维分布区间内分层抽样,在每个抽样空间等概率抽取独立随机数,这样有效减少模拟次数,大大提高了抽样模拟效率[11].
2 计算模型
2.1 随机几何初始缺陷
在结构中分别引入框架柱顶侧移和初始弯曲的随机变量uo和vo,框架梁的初始弯曲随机变量wo[12].由于结构的初始缺陷随机性由单个构件的独立随机缺陷之和引起,可将各随机变量假设为正态分布,则第i根柱初始随机侧移uoi和随机弯曲voi的概率密度分别为
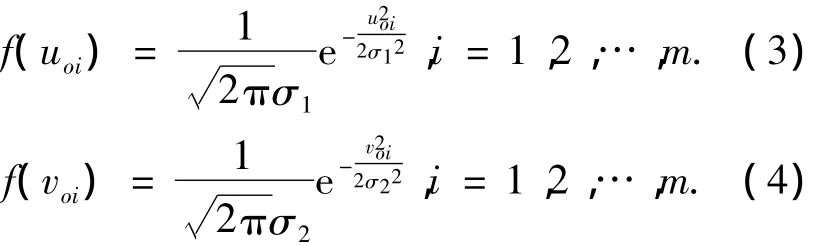
第i根梁的初始随机弯曲变量woi的概率密度为
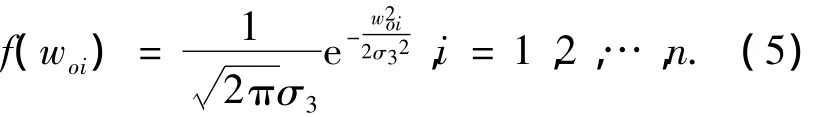
式中:m、n分别为框架柱和梁的数量;均方差σ1= σ2=h/980[13-14];σ3=l/980 .
根据失效概率pf与可靠指标β的关系,当可靠指标β=1时,可得
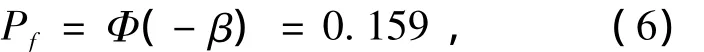
取相对误差一般为ε≤0.2,则样本数N为
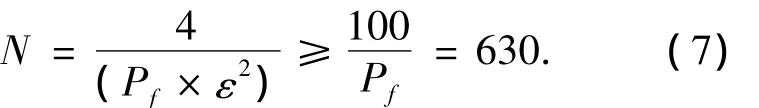
由此确定每个随机变量计算的样本数为650.
根据上述缺陷随机变量的概率密度函数,采用自编Matlab语言实现蒙特卡罗法拉丁超立方抽样.以 GB50205—2001[9]规定的单节柱垂直度及构件弯曲矢高允许偏差为依据,取规范允许值的1.05倍作为随机初始缺陷的样本限值,分别抽取框架柱顶初始侧移、柱初始弯曲和梁初始弯曲的随机缺陷值,每个随机变量的抽样数量均为650.
2.2 有限元模型
以30层双跨框架为计算模型,高宽比设计为5,柱距为8 m.各层梁柱的优化归并结果见表1,为减轻结构自重,框架柱选择箱形截面,框架梁采用焊接工字钢.选取一榀框架计算的荷载标准值汇集见图3,假设基本风压为0.30 kN/m2.
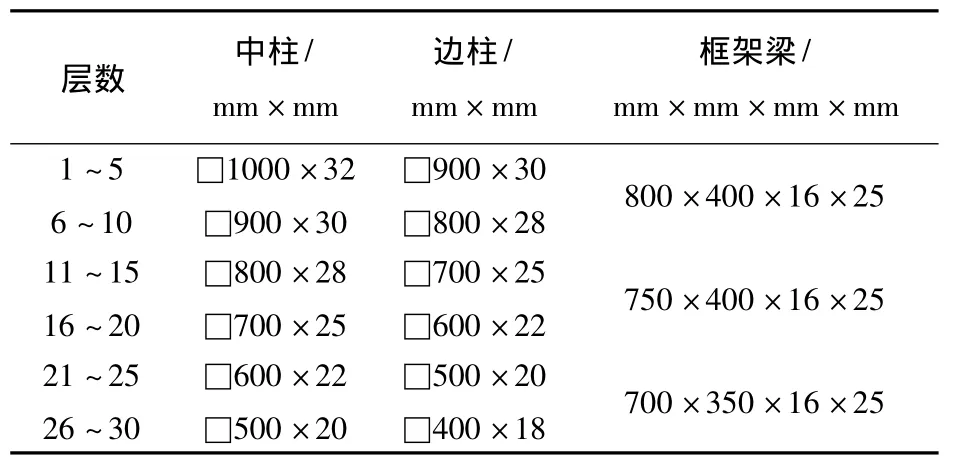
表1 框架构件尺寸
采用ANSYS有限元软件中Beam188单元模拟框架,钢材的屈服强度取fy=345 N/mm2,本构关系为双线性强化模型.为引入框架随机初始缺陷,将每根柱划分为20单元,每跨梁50个单元.假设第i根柱的初始侧移缺陷为式(8)所示的有一定斜率的直线
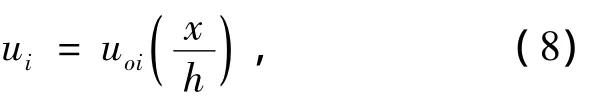
第i根柱的初始弯曲缺陷为正弦半波曲线
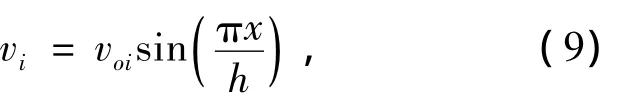
假设第i根梁的初弯曲缺陷也为正弦半波曲线
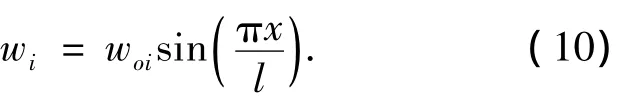
式中:uoi为蒙特卡罗法抽取第i根柱的随机初始侧移;voi和woi分别为第i根柱和第i根梁的随机初始弯曲.各梁柱单元坐标通过式(8)~(10)的缺陷分布叠加确定,由此建立了考虑结构整体和局部构件随机缺陷的框架有限元模型.
2.3 框架变形的概率统计
按荷载基本组合1.2×D+0.7×1.4×L+1.4×W,对650个添加随机缺陷的框架模型进行全过程分析,其中D为永久荷载标准值,L为可变荷载标准值,W为风荷载标准值.当荷载加载完成时结构有收敛解,此时框架部分构件应力水平较高,但未达到屈服强度设计值.
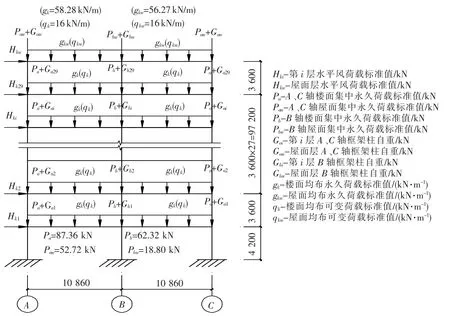
图3 框架荷载标准值
同时按荷载标准组合1.0×D+1.0×0.7×Q+1.0×W验算结构的变形是否满足正常使用极限状态的要求,采用自编后处理程序提取650个样本模型各层柱顶侧移及梁的跨中挠度.
图4和图5为框架顶层的位移概率密度直方图,分析结果表明,图4中柱顶侧移的概率密度函数f(x)为正态分布
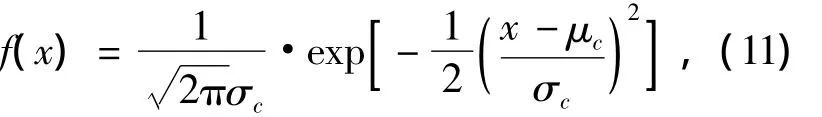
其分布函数F(x)为
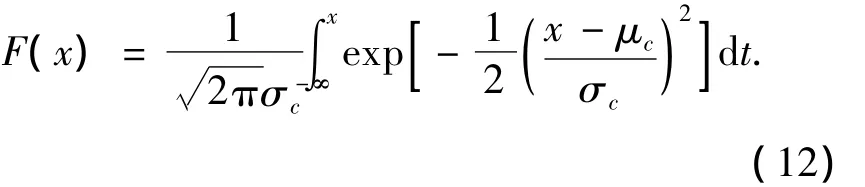
式中:μc为柱顶侧移样本均值;σc为样本均方差.
由概率密度的意义可知,样本x落在每个直方宽度区间上的概率近似等于概率密度f(x)乘以单个直方宽度Δx,即f(x)Δx,且f(x)在整个分布区间上的积分面积等于1.
式(13)为顶层框架梁跨中挠度的概率密度,也呈正态分布(见图5).
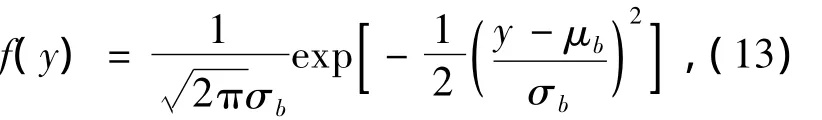
其分布函数为
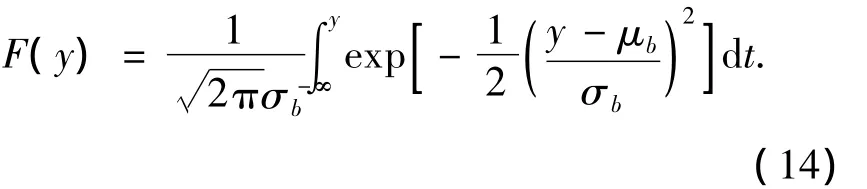
式中:μb为梁跨中挠度样本均值;σb为样本均方差.
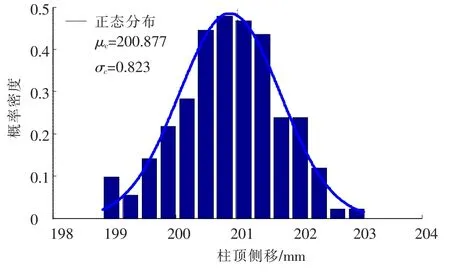
图4 屋面层柱顶侧移概率密度
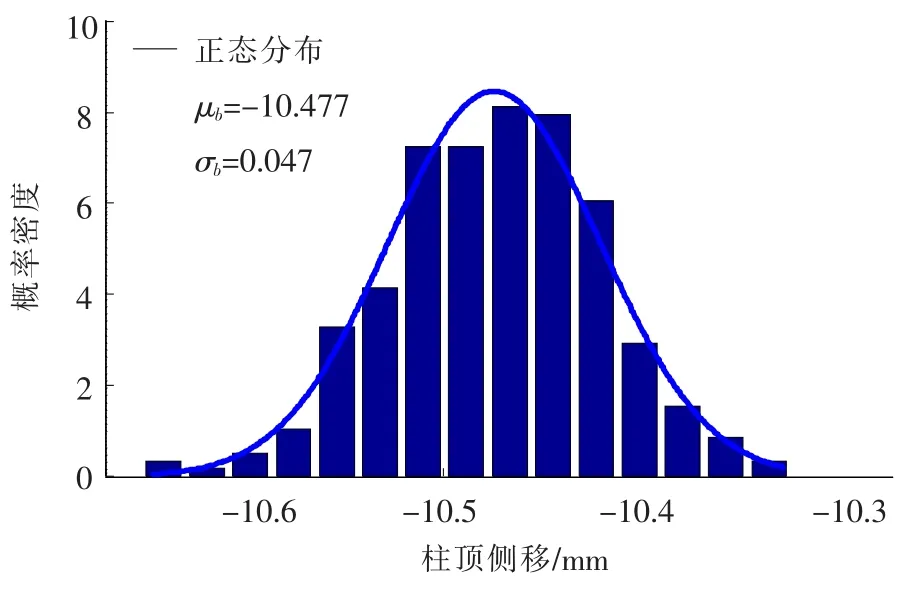
图5 屋面层跨中挠度概率密度
根据屋面层框架位移的分布函数F(x)和F(y),分别确定当置信度为95%时的特征值xα=202.203 mm和yα=-10.555 mm作为框架屋面层柱顶侧移和梁跨中挠度,此时α=0.05,见图6.同理,通过概率统计确定框架各层柱顶侧移及梁跨中挠度也均成正态分布.
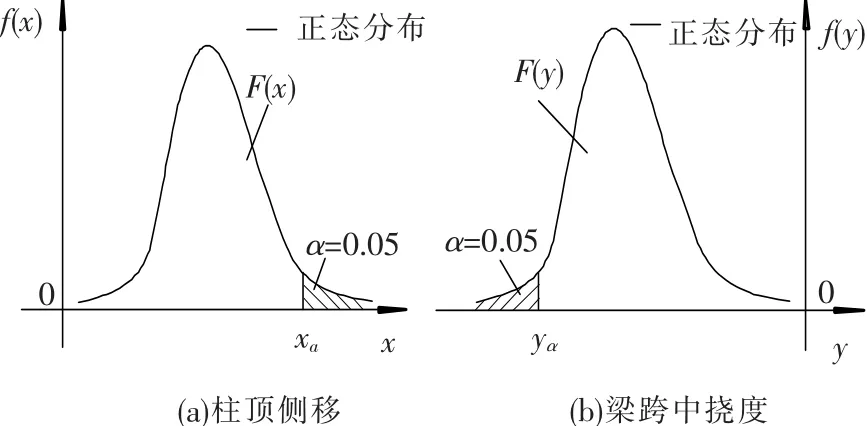
图6 框架位移特征值
2.4 几种分析方法的对比
为研究考虑不同初始缺陷对结构变形性能的影响,在相同荷载条件下,对比分析了1.2节按欧洲规范[5]和规范[9]添加直接缺陷以及规范[8]在柱顶施加假想水平力的方法.缺陷直接模拟时将各缺陷布置在与水平荷载和重力荷载相同的方向(见图7),缺陷幅值见表2.欧洲框架和中国框架分别添加了按规范计算的构件初侧移及初弯曲的框架,此时2种框架的顶层累积偏差均已超过了结构整体垂直度的允许值(H/2 500+10)[9].此外,还对无初始缺陷的理想框架进行了一阶弹性分析和二阶弹塑性分析.
上述几种方法计算的框架柱顶位移及层间相对侧移见图8、9,采用不同分析方法及初始缺陷对框架变形性能有较大影响.对比一阶弹性分析计算的柱顶侧移,二阶位移增量都相当明显不容忽视.相对一阶变形,蒙特卡罗法二阶分析的侧移增加了12.52%,假想水平力法增加了30.48%,其他缺陷考虑方法的位移增幅在两者之间.
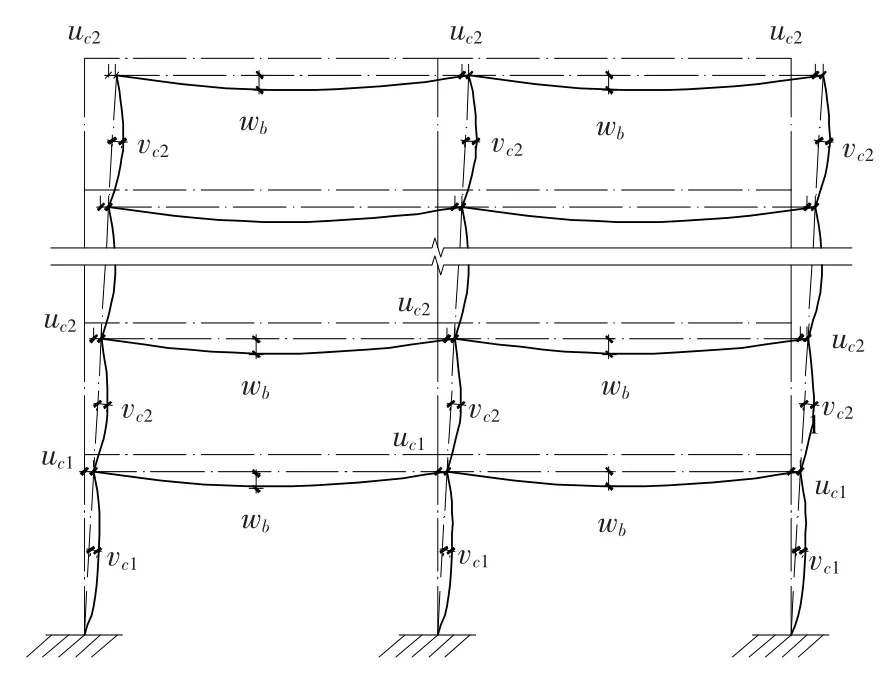
图7 初始缺陷最不利分布
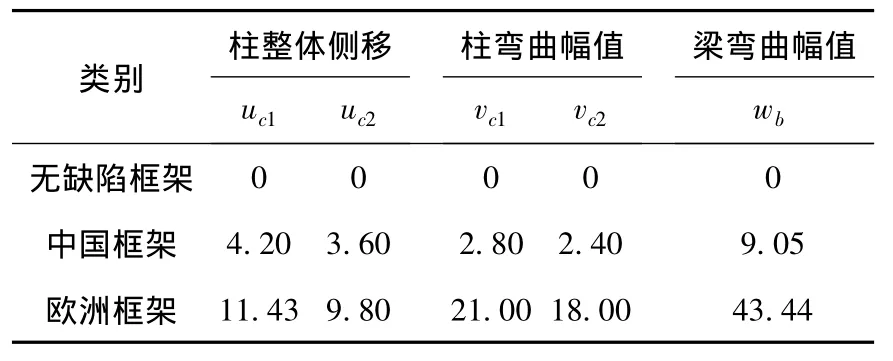
表2 构件初始缺陷计算值mm
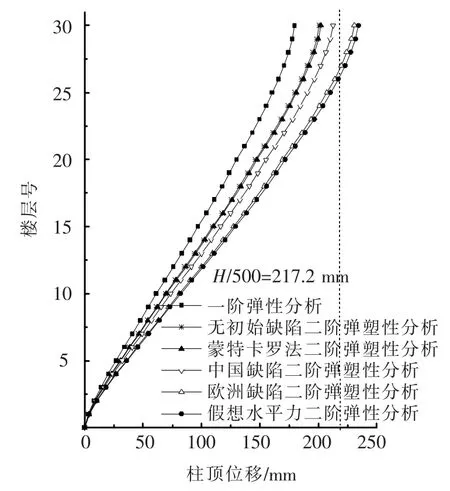
图8 框架各层柱顶位移
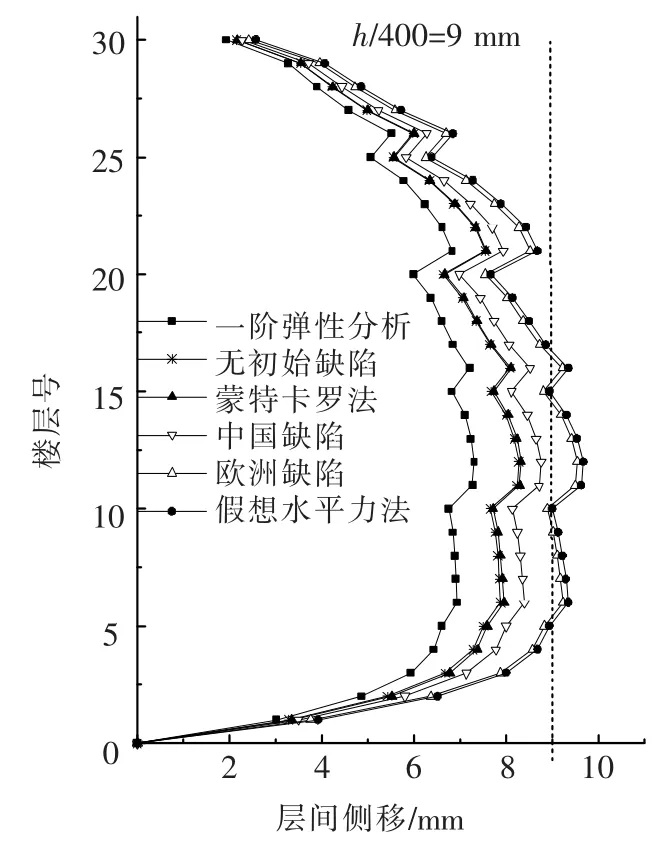
图9 框架各层层间相对位移
同为二阶分析时,蒙特卡罗法的柱顶侧移比假想水平力法,欧洲框架和中国框架的计算结果分别降低了15.96%,14.06%和5.06%;但与无初始缺陷理想框架相比,考虑随机缺陷的框架侧向变形略有增加但增幅有限(仅为0.69%),这说明蒙特卡罗法考虑缺陷随机性更符合真实缺陷的分布,并且这种缺陷分布对结构的非线性影响很小甚至可以忽略.此外,采用不同的分析方法计算的梁跨中挠度差别很小,且都在挠度容许值之内,后文不再赘述.
2.5 结构达到极限承载力时框架变形
为得到结构整体的极限承载力,对该框架进行了二阶弹塑性全过程分析,将图3汇集荷载作为施加在框架上的基准荷载,分多个荷载步逐步施加,每步施加的荷载称为该基准荷载的荷载因子.直至结构破坏时,最大的荷载因子与基准荷载的乘积即为结构的极限承载力.
框架考虑不同缺陷分布计算的极限荷载因子见图10,此时结构均已进入了弹塑性阶段,由于欧洲框架模型添加的初始几何缺陷最大,其计算的极限荷载因子最小为1.293,比无缺陷框架降低了1.82%,此时结构的极限承载力最低,但总体来说不同缺陷分布对框架极限承载力影响不明显.
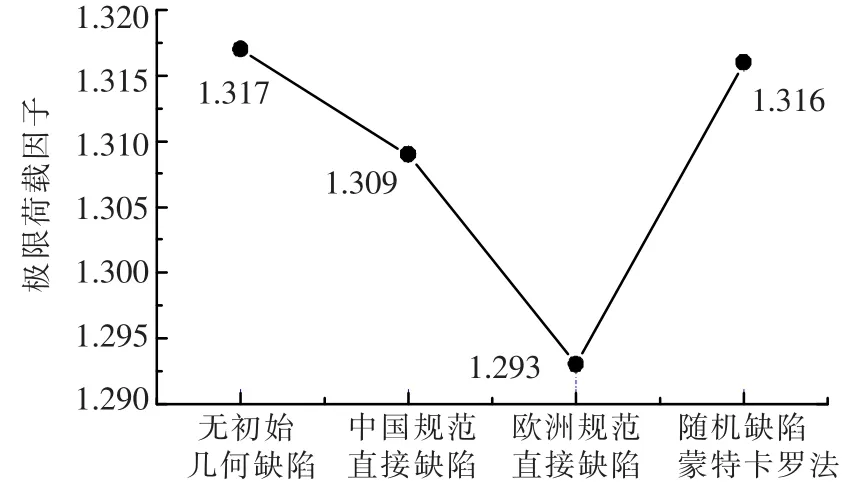
图10 极限荷载因子
统一取蒙特卡罗法统计的随机缺陷框架的极限荷载因子1.316,乘以1.0×D+1.0×L+1.0×0.6×W标准荷载组合,得到各种缺陷分布下框架各层柱顶位移(图11)和层间侧移曲线(图12),其中考虑随机缺陷的框架仍采用蒙特卡罗法统计结构变形,见图13和图14.从比较结果看,极限承载力状态下框架的二阶效应更加明显,随机缺陷框架侧移比一阶变形增加16.89%,但相比无缺陷框架侧移仅增加0.70%.
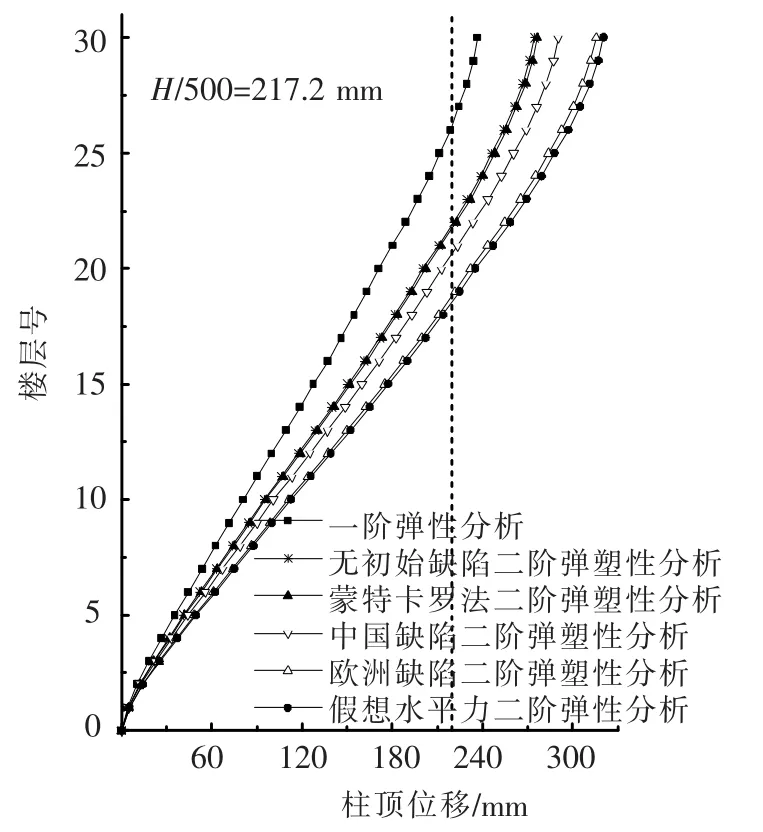
图11 框架各层柱顶位移
几种方法得出的柱顶侧移中仅一阶变形就超过了水平位移容许值8.83%,其他二阶位移更远远高出其限值(H/500)[8].因此,按承载能力极限状态设计框架会高估结构的实际承载能力,该框架的允许承载力是由正常使用极限状态的位移限值控制.
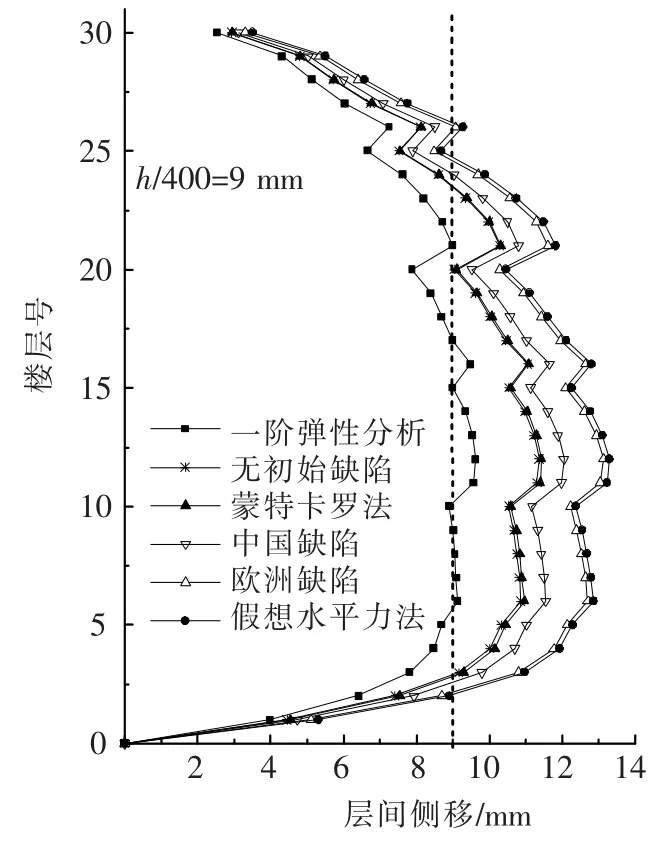
图12 框架各层层间相对位移
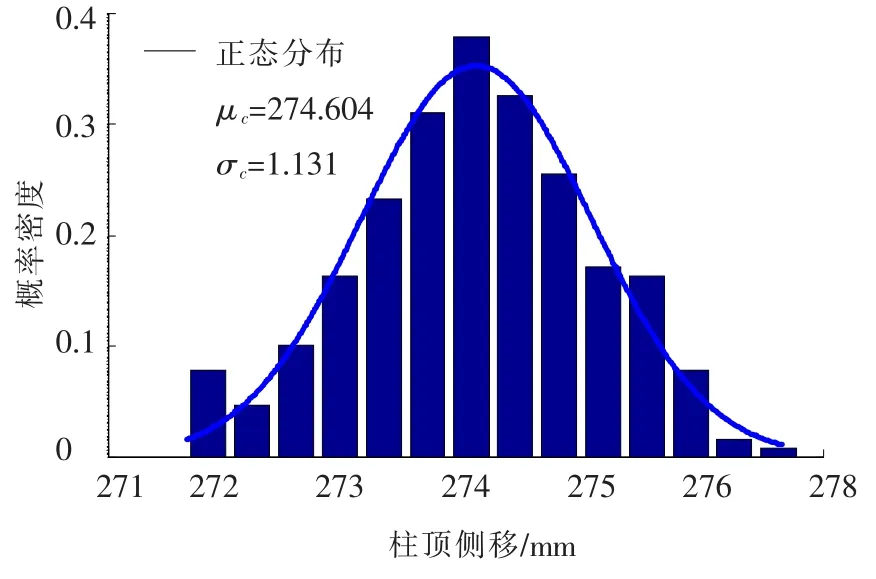
图13 屋面层柱顶侧移概率密度
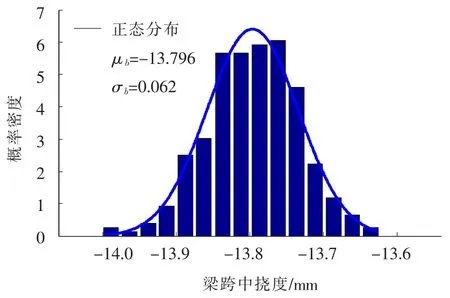
图14 屋面层跨中挠度概率密度
3 实用高等设计方法的提出
3.1 结构的适用性
近年来高层、超高层结构不断涌现,钢结构正常使用极限状态和非结构构件的适用性分析显得尤为重要.目前规范对正常使用极限状态变形限值的规定以人为经验及实际需要为主.目前各国规范多以一阶分析计算变形,但结构进行高等分析时表明,即使一阶变形在限值范围内,二阶变形也可能影响到结构的适用性或非结构构件的安全性,因此在高等分析与设计中应采用二阶变形确定是否满足正常使用极限状态的要求.
3.2 初始缺陷的随机性
蒙特卡罗法考虑的随机缺陷分布可以认为是框架缺陷的真实分布,随机缺陷框架的变形性能接近于无缺陷理想框架的计算结果.这说明真实框架初始缺陷的随机分布对结构非线性影响很小,甚至随着层数的增加,这种影响因各缺陷间的遇合作用可以忽略.因此当结构达到一定高度或层数时,高等分析与设计可以不考虑结构整体和构件的初始几何缺陷,同样能保证结构设计的真实性和安全性,并使设计过程趋于简单.
3.3 基于变形性能的高等设计方法
目前国内外关于高等分析的设计方法均基于承载能力极限状态的全过程分析,此时结构构件弹塑性充分发展,却不能保证其变形验算满足正常使用状态的要求.本文研究表明,框架的截面设计基本上受正常使用极限状态的变形性能控制.
由此提出一种实用的基于变形性能的多高层钢框架结构高等设计方法.对由正常使用极限状态控制的框架,可首先进行荷载标准组合下二阶弹塑性全过程分析,研究框架的二阶变形性能;如果此时框架变形未超过正常使用极限状态的位移限值,再对荷载基本组合下框架承载力的性能进行二阶弹塑性验算.在承载力分析中,只要基本荷载加载完成时求解收敛,结构即被认为满足承载能力的要求.该方法调换了两种极限状态的设计次序,可避免大量重复验算工作,简化设计过程.
4 结论
1)蒙特卡罗法可以预测真实框架初始缺陷的随机分布.考虑随机初始缺陷的框架柱顶位移和梁跨中挠度均呈正态分布.
2)框架二阶弹塑性分析计算的侧移比一阶分析显著增加,其二阶效应不可忽视.在高等设计中,应根据二阶变形判断结构位移是否满足正常使用极限状态的要求.
3)结构和构件初始缺陷的随机分布对结构非线性影响很小,通过概率统计确定的变形性能接近于无缺陷框架的结果,在高等设计时可不考虑.
4)提出一种实用的基于变形性能高等设计方法.首先在荷载标准组合下研究框架的变形性能,再验算基本组合下框架的承载能力.若框架变形未超过位移限值,且进行承载能力计算时求解收敛,结构即被认为同时满足两种极限状态要求.
致谢:文中结构构件缺陷实测值的统计依据杭萧钢构股份有限公司和浙江东南网架股份有限公司提供的施工质量验收记录.
[1]KIM S E,CHEN W F.Practical advanced analysis for unbraced steel frame design[J].Journal of Structural Engineering,1996,122(11):1259-1265.
[2]ZHANG Yaochun,JIN Lu,SHAO Yongsong.Practical advanced design considering random distribution of initial geometric imperfections[J].Advances in Structural Engineering,2011,14(3):387-397.
[3]日本建筑构造技术者协会.日本结构技术典型实例100选——战后50余年的创新历程[M].腾征本,腾煜先,周耀坤,等译.北京:中国建筑工业出版社,2005:170-173.
[4]American Institute of Steel Construction.AISC360-05.Specification for structural steel buildings[S].Chicago:AISC Committee,2005.
[5]European Committee for Standardization.EN1993-1-1.Design of steel structure Part1:General rules and rules for buildings[S].Brussels:Commission of European Communities,2003.
[6]British Standard.BS5950.Structural use of steelwork in buildings Part 1:Code of practice for design[S].London:British Standards Committee,2003.
[7]Hong Kong Code.Code of practice for the structural use of steel[S].The Government of the Hong Kong Special Administrative Region:Buildings Department,2005.
[8]GB 50017—2003钢结构设计规范[S].北京:中国计划出版社,2003.
[9]GB 50205—2001钢结构工程施工质量验收规范[S].北京:中国计划出版社,2002.
[10]NOWAK S N,COLLINS K R.Reliability of structures[M].New York:The McGraw-Hill Companies,2005:71-73.
[11]OLSSON A,SANDBERG G,DAHLBLOM O.On latin hypercube sampling for structural reliability analysis[J].Structural Safety,2003,25(1):47 -68.
[12]金路,张耀春,赵金友.钢框架高等分析中初始几何缺陷的考虑方法[J].建筑钢结构进展,2010,12(3):19-26.
[13]童根树.柱间水平撑杆设计方法[J].西安冶金建筑学院学报,1986,20(3):110-140.
[14]张耀春,金路,邵永松,等.考虑缺陷随机分布的钢框架变形性能研究[J].建筑结构学报,2010,31(增刊1):1-6.
