一阶线性模糊微分方程的模糊结构元解法

王 磊， 郭嗣琮

（1.辽宁工程技术大学 基础教学部，辽宁 葫芦岛 125105；2.辽宁工程技术大学 理学院，辽宁 阜新 123000）

在科学和工程中很多问题都是用模糊微分方程模型来刻画的，大部分模糊微分方程的解都要满足模糊初值条件，而模糊微分方程的研究主要是利用模糊值函数的导数。文献［1］提出了模糊导数的概念；文献［2］作了进一步的研究；文献［3］利用Hukuhara导数研究了初值问题，在此基础上文献［4］研究了解的存在唯一性。然而利用Hukuhara导数会使得解的模糊度越来越大，为了克服这一缺点，文献［5－6］提出了微分闭包的方法，将模糊微分方程转化成一簇微分闭包进行研究；文献［7－8］利用Zadeh扩展原理在一定条件下将普通常微分方程的解扩展为模糊微分方程的解，而这2种方法的缺点是没有利用模糊值函数导数。为了克服以上缺点，在Hukuhara导数的基础上，文献［9－10］提出了推广Hukuhara导数的概念，在推广Hukuhara导数的基础上文献［11］研究了二阶方程解的存在性；文献［12］研究了n阶线性方程的解；文献［13］利用等距同构映射提出了π导数的概念并研究了一阶方程的解，证明了该导数同推广Hukuhara导数是一致的；文献［14］借助于模糊数空间的嵌入定理，将模糊微分方程的模糊初值问题转化为某一Banach空间的闭凸锥中的抽象微分方程的初值问题进行研究，文献［15－16］讨论了以上不同求解方法之间的关系。上述求解方法中用到模糊数和模糊值函数都涉及λ－截集，这给运算带来了不便，文献［17］提出了模糊结构元的方法，该方法有效克服了这个困难。文献［18］利用结构元方法研究了一类模糊微分方程，在此基础上本文利用该方法研究了一阶线性模糊微分方程的模糊初值问题，证明了解的存在唯一性，并给出了方程解的模糊结构元的解析表示，说明模糊结构元方法是克服模糊微分方程解的解析表达困难的一个有效工具。

1 基本概念

作为本文的预备知识，下面简单介绍模糊结构元方法及相关结论［17］。

定义1 设E为实数域R上的模糊集，隶属函数记为E（t），t∈R。称E为R 上的模糊结构元，如果E（t）满足性质：① E（0）＝1；② 在区间［－1，0）上E（t）是单增右连续函数，在区间（0，1］上是单降左连续函数；③ 当－∞＜t＜－1或者1＜t＜＋∞时，E（t）＝0。称E为正则模糊结构元，若模糊结构元E 满足：对于∀t∈（－1，1），E（t）＞0；在区间［－1，0）上E（t）是连续且严格单调增的，在区间（0，1］上是连续且严格单调降的。

定理1 设E是R上的任意模糊结构元，又设函数f（t）在区间［－1，1］上是单调有界的，（t）是f（t）的延拓集值函数，则（E）是R 上有界闭模糊数，且（E）的隶属函数为E（f－1（t）），这里f－1（t）是f（t）关于变量t和y 的轮换对称函数（若f（t）是连续严格单调的，则f－1（t）是f（t）的反函数）。

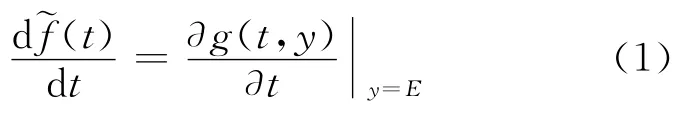
定义2 设g（t，y）＝f（t）＋ω（t）y，其中f（t）和ω（t）在T 上有界，且ω（t）非负，称g（t，y）为变量y的线性函数。易知g（t，y）是关于y在［－1，1］上的单调有界函数，由定理2，则（2）式称为T上的一个由模糊结构元E线性生成的模糊值函数，即

其中，f（t）为平移函数；ω（t）为伸缩函数。特殊地，当f（t）和ω（t）≥0都为常数时，则称其为由模糊结构元E线性生成的模糊数。

由模糊结构元E线性生成的模糊数全体用RE表示。文献［19］证明了对于任何有界模糊数或模糊值函数，均存在一个模糊结构元，使其能够由这个结构元线性生成。

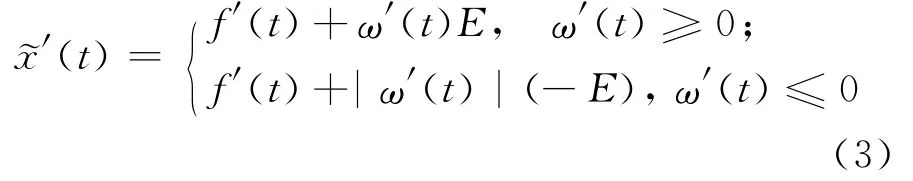
2 解的存在性和唯一性

一阶线性模糊微分方程为：

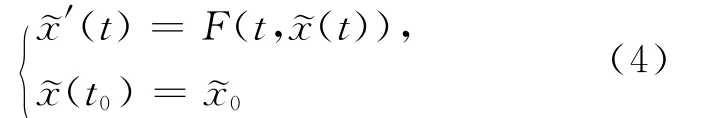
因为（4）式为线性方程，所以函数F（t，（f（t）＋ω（t）E））可以被分解成如下形式：

由（5）式可知，（4）式被表示为2个一阶线性常微分方程，则（4）式与（5）式是同解的，下面的定理说明了这一点。

定理4 对于（4）式，其中F：［t0，t0＋a］×RE→RE，若下面（1）、（2）条件满足，则（4）式与（5）式是同解的。

（1）F－ （t，f（t），ω（t）），F＋（t，f（t），ω（t））关于t为等度连续函数，即当：‖（t，f（t），ω（t））－（t1，f1（t），ω1（t））‖ ≤δ 时，有｜F±（t，f1（t），ω1（t））－F±（t，f2（t），ω2（t））｜≤ε。

（2）存在L＞0，满足：

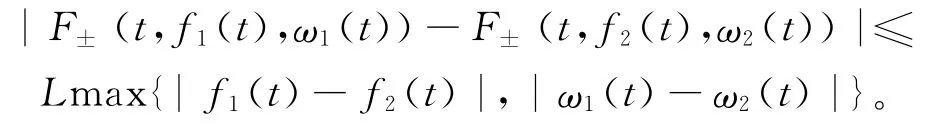
证明 首先说明（4）式与（5）式解的存在唯一性。

由常微分方程理论知条件（2）保证了（5）式解的存在唯一性。条件（1）的连续性保证了函数F（t，x（t））的连续性，又由条件（2）得：

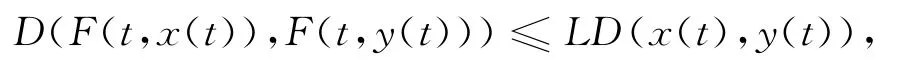
此式即为模糊微分方程的Lipschitz条件，保证了（4）式解的存在唯一性。

下面说明（4）式与（5）式为同解方程。假设˜x（t）＝f（t）＋ω（t）E为（4）式的解，将其带入（4）式即得（5）式，所以f（t）和ω（t）为（5）式的解；反之，若f（t）和ω（t）为（5）式的解，令˜x（t）＝f（t）＋ω（t）E，因为：

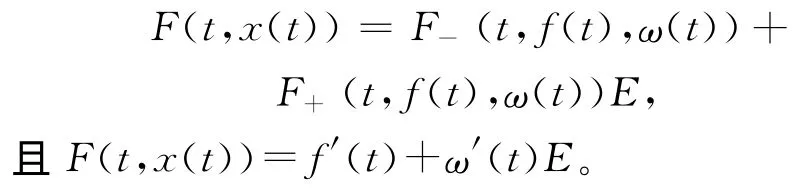
3 结构元解法与其他方法比较

首先讨论利用结构元方法与利用Zadeh扩展原理及方法之间的关系，令U 是R的子集，假设x（t，x0）是常微分方程（6）式的一个解，即

其中，x0∈U。x（t，x0）在U 上为连续函数，于是定义映射：

令Lt（x0）＝x（t，x0）是（6）式的唯一解且关于点x0是连续函数，于是对Lt作扩展得：

定理5 利用结构元方法与利用Zadeh扩展原理求解（4）式所得结果一致。

证明 由Zadeh的扩展原理解得（4）式的解为：

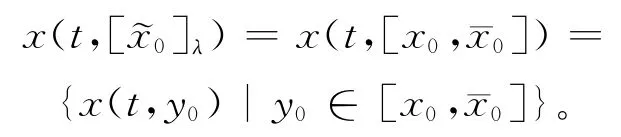
利用结构元方法解得（4）式的解为：

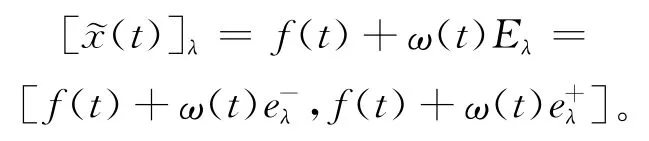
由（5）式知，f（t）和ω（t）为同一常微分方程分别在初值m和n条件下的解，而由Zadeh的扩展原理知该常微分方程在初值x0的条件下的解为x（t，x0），所以将f（t）和ω（t）分别记为f（t）＝x（t，m）和ω（t）＝x（t，n），于是：

本文借助定理5给出结构元方法同其他方法之间的关系。

定理6 利用结构元方法与利用微分闭包求解（4）式所得结果一致。

证明 文献［7］证明了利用Zadeh扩展原理与利用微分闭包求解（4）式所得结果一致，由定理5，知结论成立。

证明 文献［13］证明了利用Zadeh扩展原理与推广Hukuhara导数求得（4）式所得结果一致，由定理5，知结论成立。

定理8 利用结构元方法与利用π导数求解（4）式所得结果一致。

证明 文献［11］证明了利用π导数与推广Hukuhara导数求得（4）式所得结果一致，由定理7，知结论成立。

4 算 例

考查下面的模糊马尔萨斯人口问题：

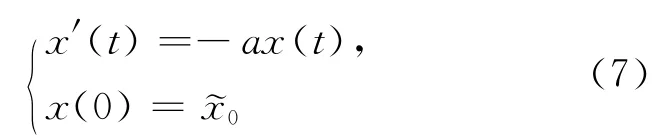
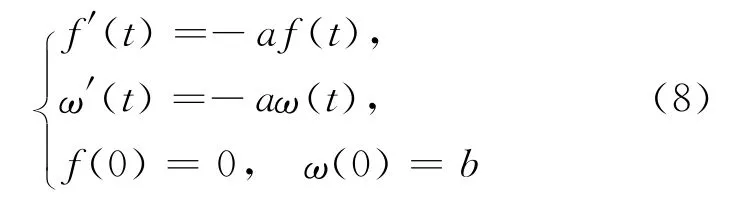
解（8）式得f（t）＝0，ω（t）＝be－at，所以˜x（t）＝be－atE，可以看出解可以解析地表示，取λ－截集得［˜x（t）］λ＝（1－λ）e－at［－b，b］，这个结果与文献［7］中利用扩展原理、文献［15］利用微分闭包、文献［10］利用推广Hukuhara导数、文献［13］利用π导数所得结果一致。在（7）式中，令a＝b＝2，将时间t＝［0，1.5］进行6等分，利用结构元方法解析给出了t在7个点处解的隶属函数，如图1所示。

图1 解的隶属函数

5 结束语

本文利用结构元方法研究了一阶线性模糊微分方程的模糊初值问题，其优点是：模糊值函数不需要重新定义导数，直接转化为2个普通函数的导数，而且方程的解可以解析地表示。文中要求ω（t）及ω′（t）非负，即伸缩函数为非负单调递增函数这一条件并不苛刻，如同文献［7，10］利用Hukuhara导数及推广Hukuhara导数求解时要求［uλ（t），vλ（t）］和 ［u′λ（t），v′λ（t）］为有效的λ－截集一样。利用结构元方法研究非线性模糊微分方程及高阶模糊微分方程是值得研究的课题。

［1］Chang L S，Zadeh L A.On fuzzy mapping and control［J］.IEEE Trans Systems Man Cybernet，1972，2：30－34.

［2］Dubois D，Prade H.Towards fuzzy differential calculus：part 3，differentiation［J］.Fuzzy Sets and Systems，1982，8：225－233.

［3］Kaleva O.Fuzzy differential equations［J］.Fuzzy Sets and Systems，1987，24：301－317.

［4］Song S，Wu C.Existence and uniqueness of solutions to the Cauchy problem of fuzzy differential equations［J］.Fuzzy Sets and Systems，2000，110：55－67.

［5］Hüllermeier E.An approach to modelling and simulation of uncertain systems［J］.International Journal of Uncertainty Fuzziness Knowledge－Based System，1997，5：117－137.

［6］Guo M，Xue X P，Li R.Impulsive functional differential inclusions and fuzzy population models［J］.Fuzzy Sets and Systems，2003，138：601－615.

［7］Misukoshi M，Chalco－Cano Y，Román－Flores H，et al.Fuzzy differential equations and the extension principle［J］.Information Sciences，2007，177：3627－3635.

［8］Allahviranloo T，Shafiee M，Nejatbakhsh Y .A note on fuzzy differential equations and the extension principle［J］.Information Sciences，2009，179：2049－2051.

［9］Bede B，Gal S G.Generalizations of the differentiability of fuzzy number value functions with applications to fuzzy differential equations［J］.Fuzzy Sets and Systems，2005，151：581－599.

［10］Bede B，Rudas I L，Bencsik A L.First order linear fuzzy differential equations under generalized differentiability［J］.Information Sciences，2007，177：1648－1662.

［11］Allahviranloo T，Kiani N A，Barkhordari M.Toward the existence and uniqueness of solutions of second－order fuzzy differential equations ［J］.Information Sciences，2009，179：1207－1215.

［12］Khastan A，Bahrami F，Ivaz K.New results on multiple solutions for nth－order fuzzy differential equations under generalized differentiability［J］.Boundary Value Problems，2009，doi：10.1155／2009／395714.

［13］Plotnikova N V.Systems of linear differential equations withπderivative and linear differential inclusions［J］.Sbornik：Mathematics，2000，196：1677－1691.

［14］Wu C X，Song S J，Lee E S.Approximate solutions，existence，and uniquencess of Cauchy problem to fuzzy differential equations［J］.Journal of Mathematical Analysis and Applications，1996，200：629－645.

［15］Chalco－Cano Y，Román－Flores H.Comparation between some approaches to solve fuzzy differential equations［J］.Fuzzy Sets and Systems，2009，160：1517－1527.

［16］Wang L，Li N.Comparation between some approaches to solve first order linear fuzzy differential equation［J］.Advances in Intelligent and Soft Computing，2010，78：95－102.

［17］郭嗣琮，苏志雄，王 磊.模糊分析计算中的结构元方法［J］.模糊系统与数学，2004，18（4）：68－75.

［18］郭嗣琮，王 磊.一类线性模糊常微分方程的模糊结构元解法［J］.辽宁工程技术大学学报，2009，28（4）：668－671.

［19］郭嗣琮.模糊数与模糊值函数的结构元线性生成［J］.辽宁工程技术大学学报，2006，25（3）：475－477.