亭子口重力坝深层抗滑稳定性分析
2011-08-29徐佳成薛维成职承杰
徐佳成,薛维成,职承杰,孙 平
(1.中国水利水电科学研究院 岩土工程研究所,北京 100048;2.长江勘测规划设计有限责任公司,湖北 武汉 430010)
重力坝深层抗滑问题是重力坝设计中的一个重要领域,其稳定分析的成果是重力坝剖面设计的主要依据[1]。据不完全统计,在我国就有92座已建、在建和设计中的大中型重力坝的坝基存在软弱结构面,其深层抗滑稳定问题受到普遍关注[2],如向家坝、三峡左岸厂房坝段、天生桥二级、铜街子、双牌、百色等水利枢纽工程都开展了深层抗滑稳定分析的研究工作[3]。
在重力坝抗滑稳定分析方法中主要有刚体极限平衡法、有限元法、地质力学模型法等,其中刚体极限平衡法发展的时间最长、理论研究及使用经验都比较丰富,目前仍然是水利行业规范中不可或缺的分析方法[4]。对坝基沿双滑面滑动的情况,水利行业混凝土重力坝规范[5]中建议采用“等K法”并给出了相应的计算公式,但对于多滑面的情况没给出明确的规定。此外,双滑面“等K法”计算式中假定的是每一滑面通过的同一种介质,当穿过多种岩层时强度参数需要做加权处理,这严重影响了该方法在理论上的严密性[2]。陈祖煜[1]基于虚功原理的基础上提出了理论体系更为严格、应用范围更为广泛的广义等K法(Sarma法),并证明了在双滑面时与等K法的等效性。自20世纪80年代以来,分项系数极限状态设计方法得到推广应用,由于分项系数是在总结了大量实例的资料和可靠度分析理论基础上所得的,因此考虑到了目标函数自变量的不确定性[2]。将分项系数极限状态设计方法应用到重力坝深层抗滑稳定中可使坝基的抗滑稳定在风险分析基础上得到改善。
亭子口重力坝坝址处发育有影响坝基深层抗滑稳定的软岩和软弱夹层,从本文分析所得到的几种滑移模式上来看滑面多为三至四段的折线且下游处的滑面穿过多种岩层,水利规范中的双滑面“等K法”显然难以满足如此复杂的计算条件。为此,本文采用适用性更广的广义等K法对亭子口重力坝表孔坝段的多种滑移模式在不同的计算工况下的深层抗滑稳定性作了验算,并与分项系数极限状态设计方法相结合从风险分析的角度探讨了该坝段的深层抗滑稳定性。此外,对重力坝深层抗滑多滑面广义计算方法中条块作用力与水平面夹角的大小对大坝深层抗滑稳定性的敏感性也作了分析。本文的分析结果表明广义等K法相比于双滑面“等K法”更适用于滑面比较复杂的坝基深层抗滑稳定性分析,与工程的实际情况也比较相符。同时,本文的稳定分析成果可为亭子口重力坝的稳定性评价提供参考依据。
1 基本原理
1.1 广义等K法计算原理Sarma法是岩质边坡稳定分析中常用的一种方法,该方法对土条进行斜分条,并假定在底滑面和倾斜界面上均达到极限平衡,据此推导出计算安全系数的公式。将该方法推广到重力坝深层抗滑稳定分析时,一般假设条块界面为垂直面且对穿越混凝土坝体部分的条块界面的黏聚力c和摩擦系数f值取为0。针对重力坝垂直条分的特殊情况,广义等K法的计算公式为[2]:
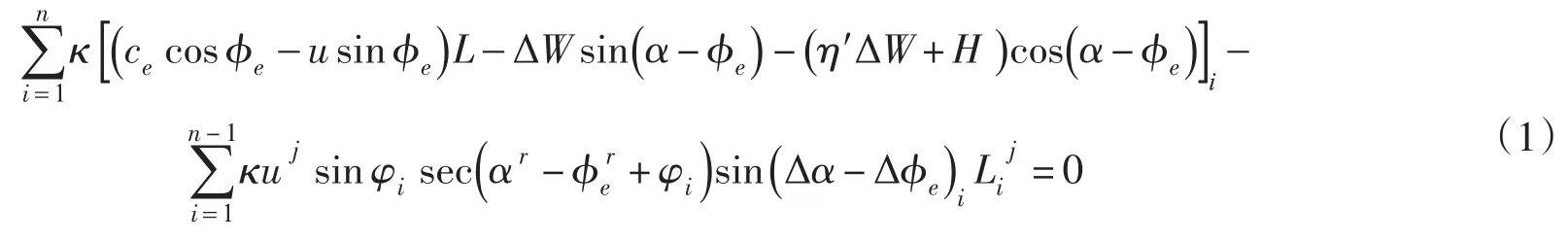
式中系数κ按下式计算:
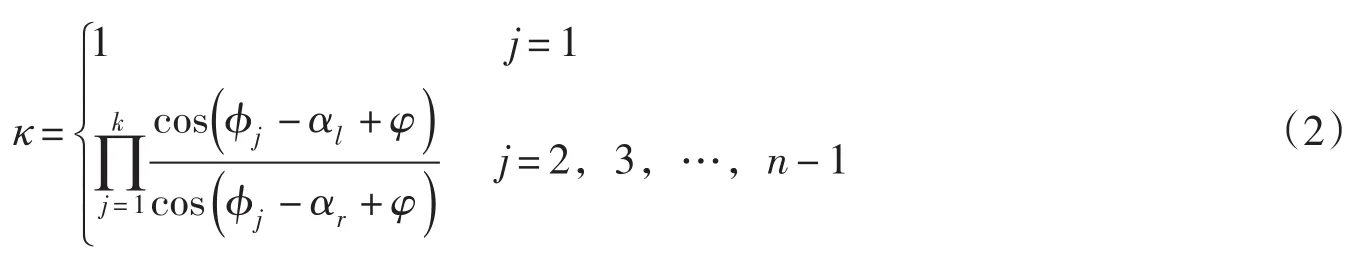
安全系数K就隐藏在式(1)中ce和φe的折减定义式中。式(1)和式(2)中各参数的含义详见文献[2]。
1.2 分项系数极限状态设计方法电力行业混凝土重力坝设计规范[6]规定使用极限状态表达式来进行结构和地基的稳定性验算,要求将建筑物抗滑稳定分析从传统的安全系数表达式改为极限状态表达式,对承载能力极限状态验算的表达式为:
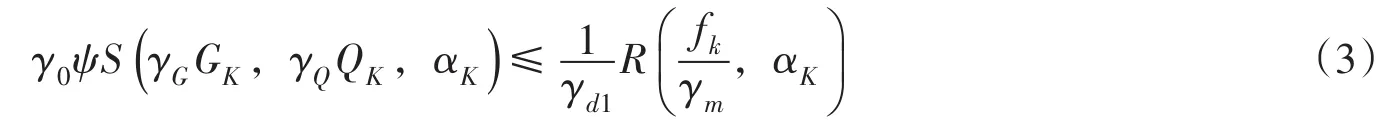
在进行重力坝抗滑稳定分析时,可以将分项系数极限状态方法的式(1)改造为使用安全系数K的表达形式:

对式(3)中的荷载和抗力各项乘上相应的分项系数μxi后,仍可按传统的极限平衡方法和强度折减意义求解安全系数K,即求解满足式(4)的K值。式(1)和式(2)中各参数的含义详见文献[6]。
2 工程概况
亭子口水利枢纽位于嘉陵江中游上段、四川省广元市苍溪县境内、苍溪县城上游约15km处,是嘉陵江干流开发中以防洪、灌溉及城乡供水、发电为主,兼顾航运等综合效益的控制性工程。该枢纽正常蓄水位458m,相应库容34.68亿m3,电站装机1 100MW。枢纽主要由大坝、电站厂房、垂直升船机和灌溉引水首部工程等组成。工程等别为Ⅰ等,工程规模为大(1)型[7]。
亭子口水利枢纽大坝为混凝土重力坝,坝顶高程465m,最大坝高116m。坝基岩体由软岩与中硬岩互层组成,分布的地层主要有白垩系下统苍溪组的砂岩、粉砂岩及黏土岩。厚层砂岩(以及)中共分布软岩31层,河床部位控制性软岩为NS2-1-5、NS2-1-8、NS2-1-9和层,软岩中软弱夹层共有31条,亭子口重力坝的典型地质剖面图如图1所示。根据坝基岩体岩层层面,层间软弱夹层或软岩,横河向与顺河向结构面,坝轴线方向的空间展布分析可知:岩层层面、软岩层或软弱夹层走向30°~60°与坝轴线夹角约40°,倾向下游约1°~5°,偏左岸,可构成坝基深层滑动的底滑面;顺河向裂隙走向330°~350°,与坝轴线方向近正交,且空间连续性好,可构成坝基深层抗滑的侧向切割面。因此亭子口水利枢纽存在以岩层层面、软岩或软弱夹层为底滑面,顺河向裂隙为侧向切割面,下游抗力体为剪出口,典型的重力坝深层抗滑稳定滑移模式,如图1所示。
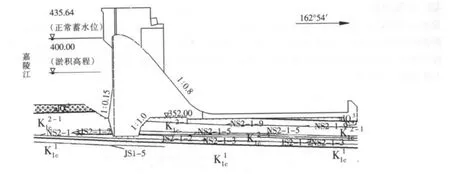
图1 亭子口重力坝典型地质剖面
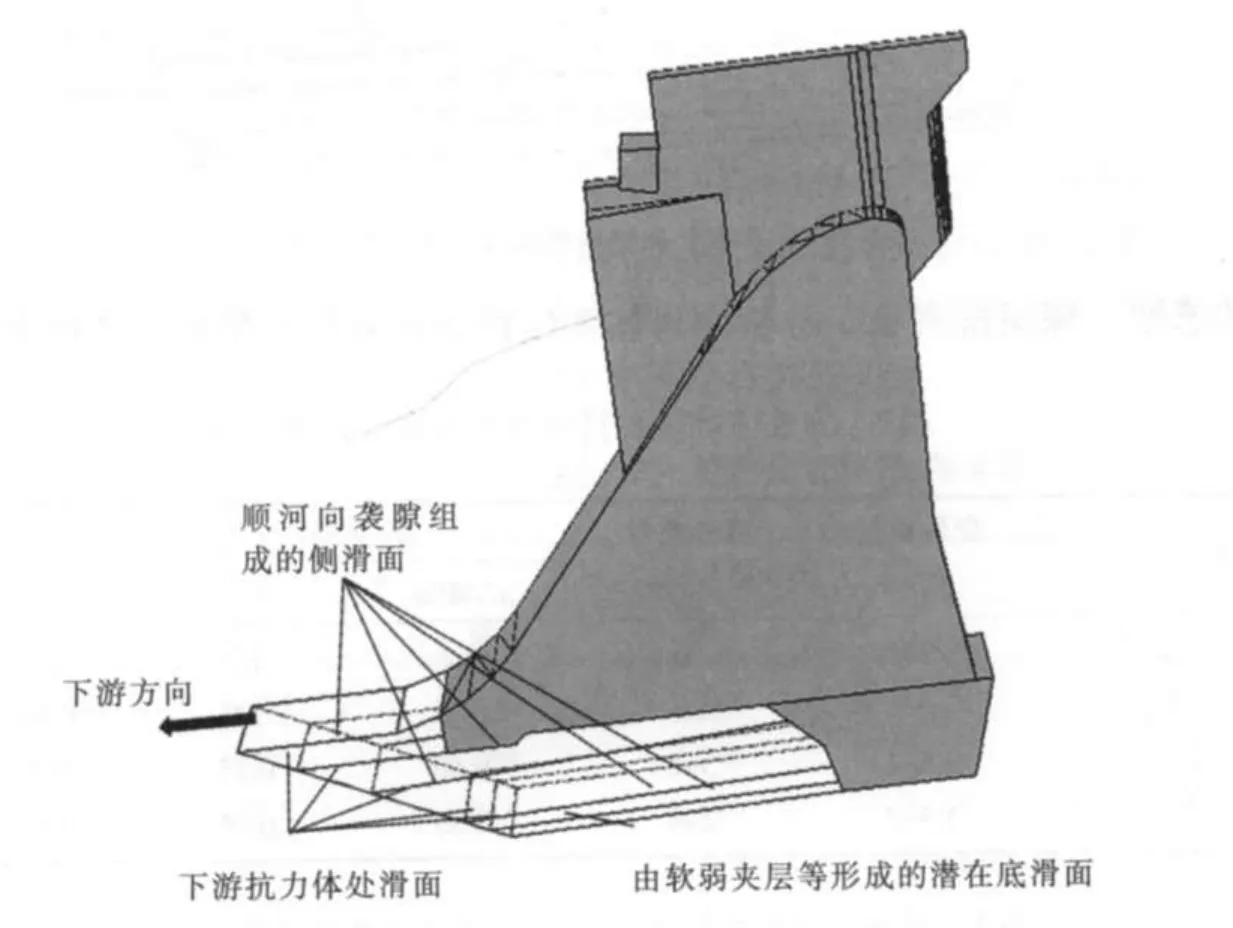
图2 亭子口水利枢纽坝基深层抗滑滑移模式示意
3 坝基深层抗滑稳定滑移模式分析
根据表孔坝段处坝基内软弱夹层与结构面发育情况,该部位的坝基深层滑动模式主要有7种,主滑面与下游基岩抗力体的组合情况见表1。

表1 亭子口水利枢纽表孔坝段坝基深层抗滑滑移模式
4 计算模型及计算条件
4.1 计算模型亭子口重力坝的二维计算模型如图3所示。模型中的上下游水压力通过上游拉裂缝充水、下游坡外水位来体现,具体方法见文献[1]。应用中国水利水电研究院开发的岩质边坡稳定分析程序EMU2010进行坝基深层抗滑稳定分析时,坝基的扬压力通过坝体和坝基中的浸润线来近似模拟,消力池底板以上的下游水体压重通过作用于消力池底板上和作用在下游水位以下坝面上的水压力来模拟,如图3。
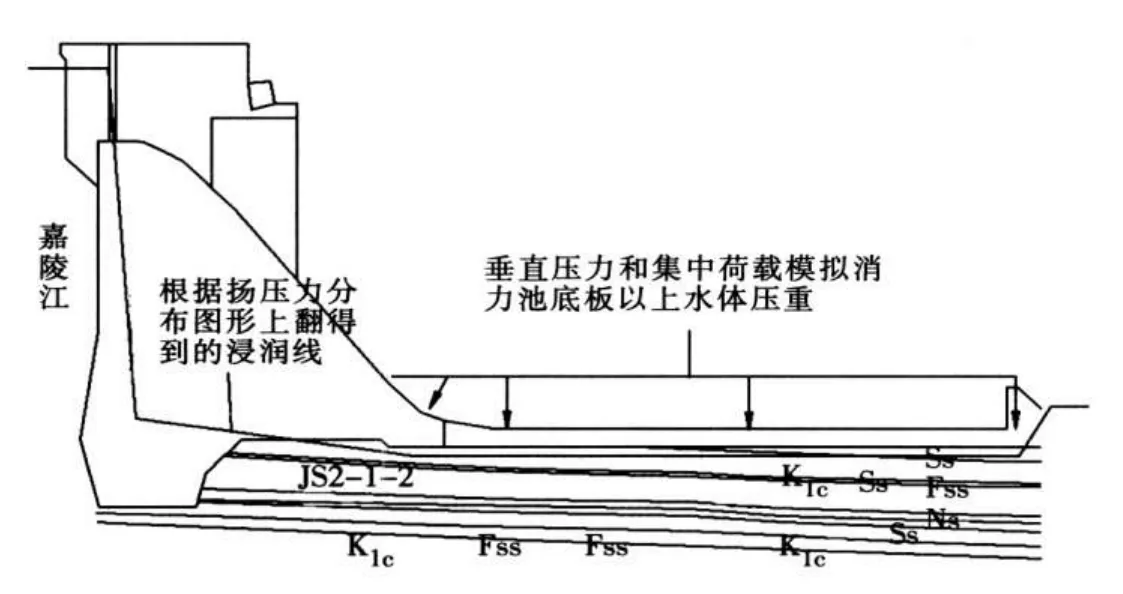
图3 亭子口水利枢纽坝基深层抗滑计算模型
4.2 计算参数的选取深层抗滑稳定分析中岩体和结构面计算采用值如表2和表3所示。

表2 坝址区岩体材料特性及力学参数建议值

表3 坝址区结构面与软弱夹层物理力学参数地质建议值
4.3 计算工况在重力坝坝基深层抗滑稳定分析中,除了近似双斜滑面的滑移模式和相应的材料物理力学性质外,水的作用对深层抗滑稳定的分析成果有着重要的影响。因此,对每一种坝基深层滑动模式,结合不同大坝运行情况,共考虑了6种计算工况,如表4所示。
5 稳定性计算成果及分析
5.1 广义等K法结算结果目前我国水利行业混凝土重力坝设计规范(SL 319-2005)[5]采用双滑面的等K法,但在多滑面的情况下,规范没有给出相应的方法。陈祖煜等[2-4]提出了基于Sarma法的广义等K法,并从理论上严格证明了在双滑面条件下等K法和Sarma法(或广义等K法)是完全等效的。广义等K法不仅理论严密,并且适合于多滑面的复杂深层抗滑稳定分析。针对亭子口重力坝表孔坝段的滑移模式,采用材料的抗剪断强度指标,并规定条块界面上强度指标c=0及条间力的倾角φ=0°,6种工况下的坝基抗滑广义等K法计算所得的稳定性计算结果见表5。
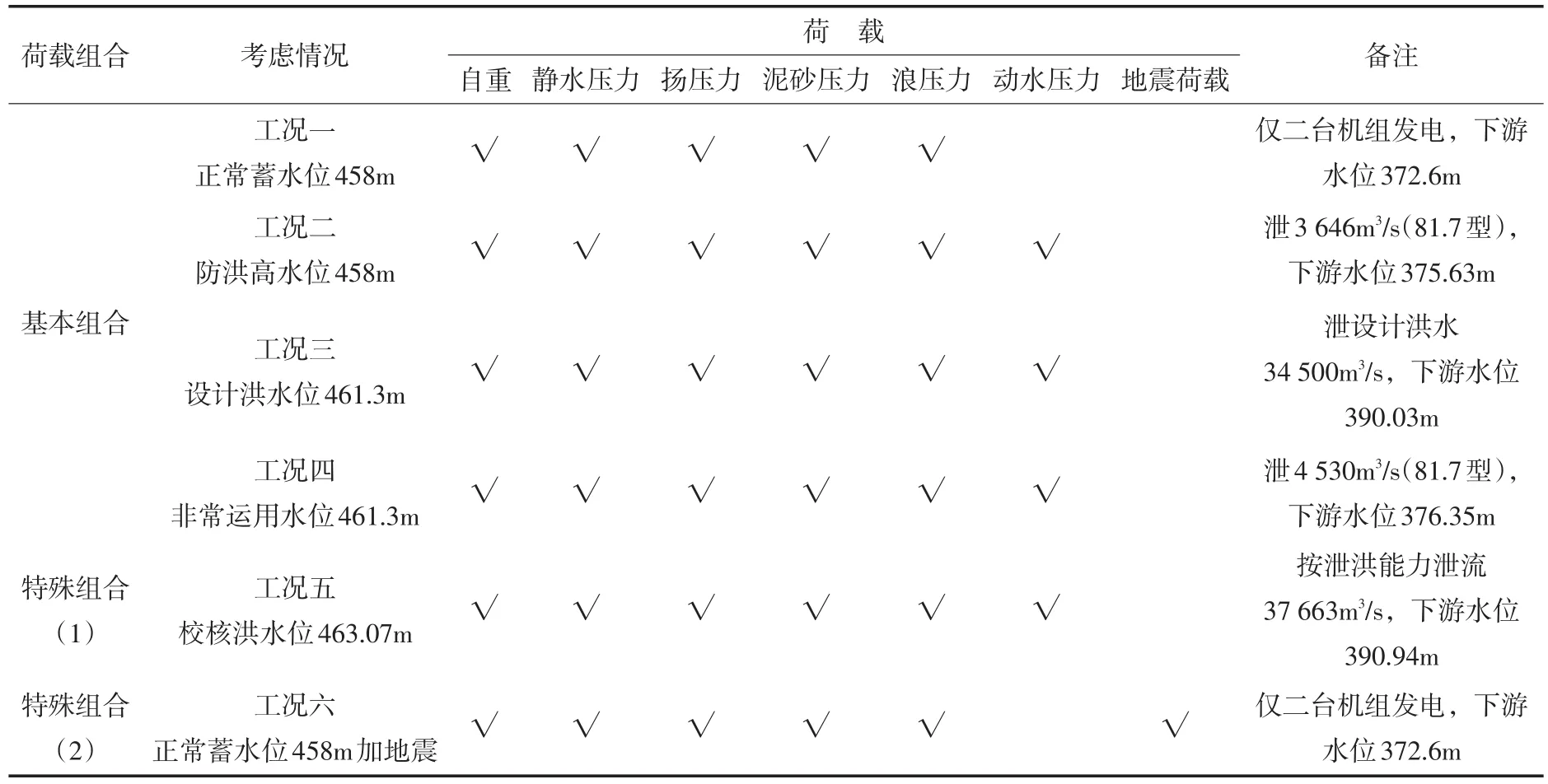
表4 亭子口重力坝深层抗滑计算工况
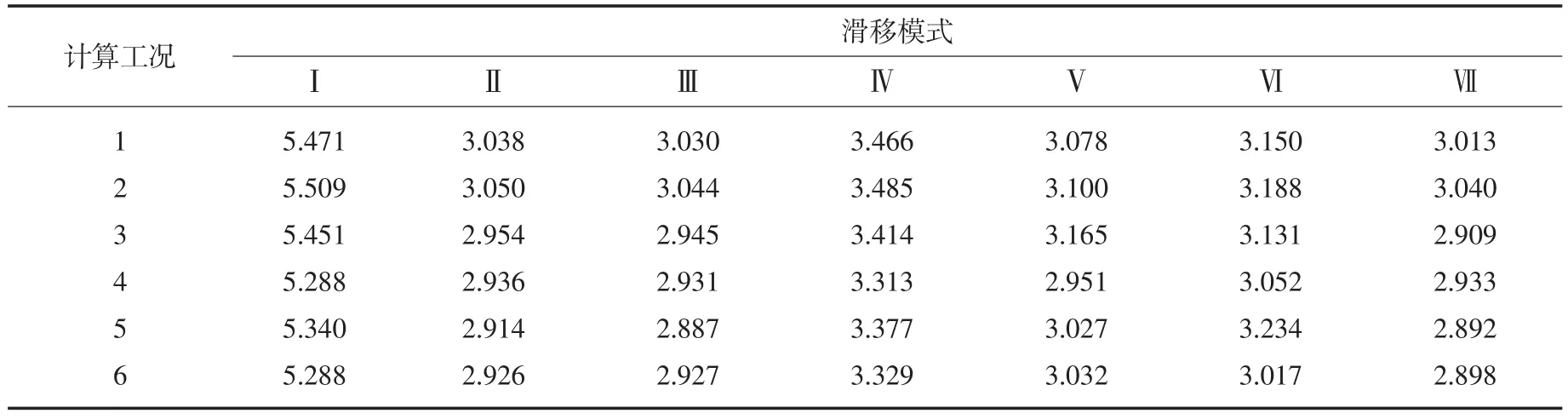
表5 表孔坝段深层抗滑稳定安全系数计算结果(等K法)
由表5可见,文中所述7种滑移模式在6种工况下(φ=0°)基本上能满足规范(SL 319-2005)中规定的基本荷载组合下大于3.0、特殊荷载组合下大于2.5的要求。需要注意的是,剪断坝体混凝土与软岩ns2-1-9顶底面组合滑动和沿坝基与泥化夹层JS2-1-2组合滑动两种滑移模式在设计洪水位、非常运用水位等基本荷载组合下最小安全系数为2.909,略小于K=3.0的标准。
5.2 水电行业规范的分项系数极限状态法计算结果电力行业的《混凝土重力坝设计规范》(DL5108-1999)[6]规定使用分项系数极限状态表达式来进行结构和地基的稳定性验算,要求将建筑物抗滑稳定分析从传统的安全系数表达式改为分项系数极限状态表达式。以文中表2和表3中提供的参数分别作为标准值,各种材料强度指标的分项系数按规范《混凝土重力坝设计规范》(DL5108-1999)选取,按照文献[2-3]建议的等结构系数法进行计算,结果见表6。
由表6的计算结果可见,亭子口重力坝表孔坝段的7种滑移模式在6种工况下的安全系数均能满足文献[2]和[3]K≥Ka=1.32的要求。
5.3 条块界面上强度指标对深层抗滑稳定分析结果的影响本文用广义等K法计算时规定了条块界面上强度指标c=0及条间力的倾角φ=0°,这一做法实际上是把重力坝处理成一系列相互之间不传递剪力的条块,是偏于保守的。为更客观的考虑条块之间的作用力,这里对条间力倾角φ的取值对亭子口重力坝表孔坝段深层抗滑稳定性的敏感性作了探讨,仅对表5中不满足规范要求的工况进行核算,计算结果见表7。
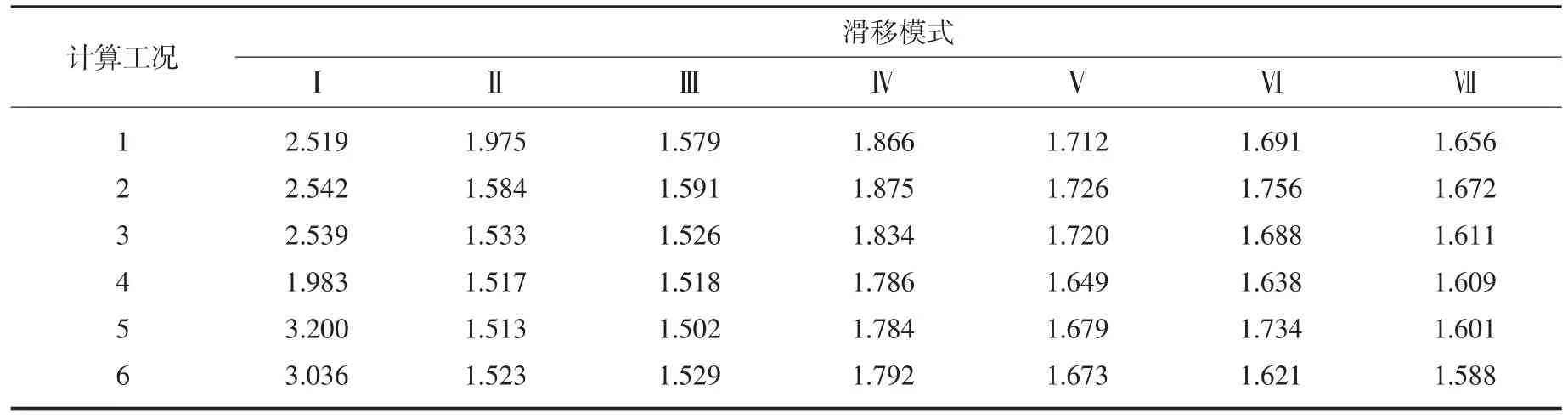
表6 亭子口重力坝表孔坝段深层抗滑稳定分项系数极限状态安全系数计算结果
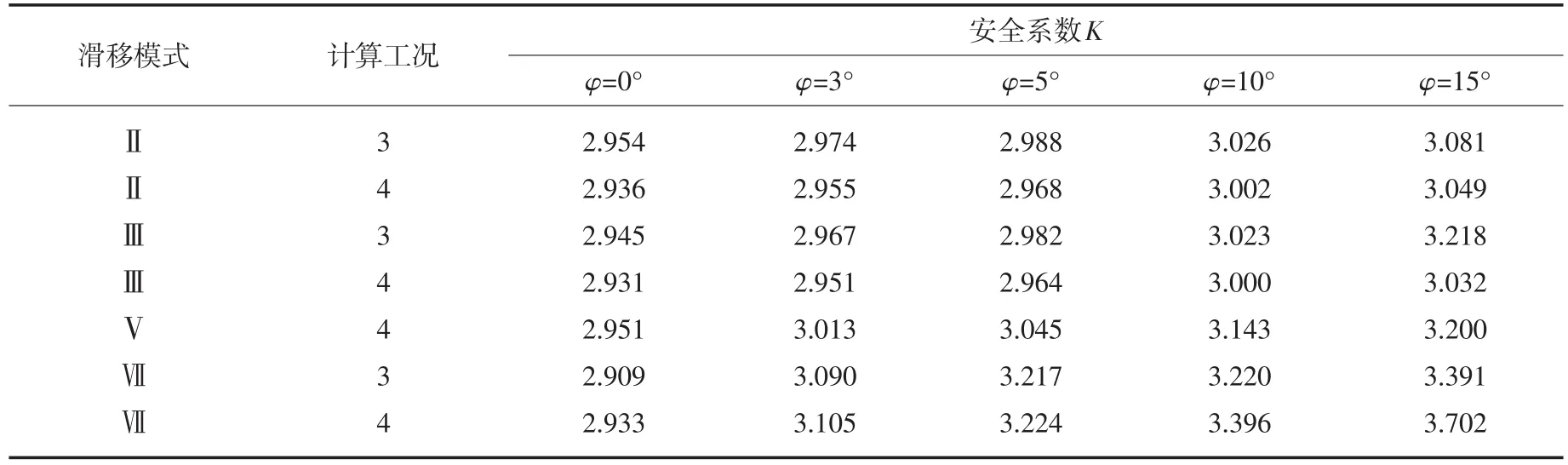
表7 条间力倾角φ对深层抗滑稳定的敏感性分析
由表7可见,亭子口重力坝表孔坝段深层抗滑稳定安全系数K随着条间力的倾角φ增大而增大;不同滑移模式下,安全系数的增长幅度也不一样;当φ从0°增加到15°时,在以上滑移模式中安全系数的增幅最大可达到20%左右;当φ等于10°时,安全系数K均能满足规范(SL 319-2005)中K≥3.0的要求。
6 结论与建议
(1)由于亭子口水利枢纽坝基部位存在倾向下游且走向与坝轴线夹角较小的软岩、岩层层面和泥化夹层,并且发育有顺河向的裂隙,因此存在重力坝深层抗滑稳定问题。从滑移模式上来看滑面多为三至四段的折线且下游处的滑面穿过多种岩层,采用广义等K法能比较好的满足该大坝复杂的计算条件。(2)根据表孔坝段的广义等K法(规定条块界面上强度指标c=0及条间力的倾角φ=0°)的稳定分析成果,当所有帷幕和排水均正常工作时,文中所述7种滑移模式在6种工况下基本上能满足规范(SL 319-2005)中规定的基本荷载组合下大于3.0、特殊荷载组合下大于2.5的要求。但剪断坝体砼与软岩ns2-1-9顶底面组合滑动和沿坝基与泥化夹层JS2-1-2组合滑动两种滑移模式在设计洪水位和非常运用水位工况下计算所得的最小安全系数为2.909,略低于K=3.0的标准。(3)按照电力行业规范(DL5108-1999)使用分项系数极限状态表达式对亭子口重力坝表孔坝段的7种滑移模式在6种工况下的验算结果表明表孔坝段的深层抗滑安全系数均能满足K≥Ka=1.32的要求。(4)广义等K法计算时条块作用力与水平面的夹角φ的取值对大坝深层抗滑稳定分析成果有明显的影响。随着条间力的倾角φ的不断增大,深层抗滑稳定安全系数不断增大,当φ从0°增加到15°时,安全系数的增幅最大可达到20%左右。根据表7的计算结果,建议在应用广义等K法对亭子口重力坝进行深层抗滑稳定核算时适当提高φ的值,本文中当φ等于10°时,安全系数K均能满足规范(SL 319-2005)中K≥3.0的要求。(5)从本文的计算结果来看,广义等K法相比于双滑面“等K法”更适用于滑面比较复杂的坝基深层抗滑稳定性分析。因此,建议对滑移模式的滑面为多段线且穿越岩层较多的坝基深层抗滑稳定性分析采用适用性更强的广义等K法。
[1]陈祖煜,汪小刚,杨健,等.岩质边坡稳定分析——原理·方法·程序[M].北京:中国水利水电出版社,2005.
[2]周建平,钮新强,贾金生.重力坝设计二十年[M].北京:中国水利水电出版社,2008.
[3]中国水利水电科学研究院.《重力坝深层抗滑稳定和处理措施研究》子题之重力坝深层抗滑稳定和处理措施有关问题研究成果报告[R].北京:中国水利水电科学研究院,2007.
[4]陈祖煜,王玉杰,徐佳成.重力坝深层抗滑稳定分析的极限平衡法[R].2010年数值物理模拟分会及岩体结构稳定性理论与方法专题研讨会,2010.
[5]中华人民共和国水利行业标准.SL 319-2005混凝土重力坝设计规范[S].北京:中国水利水电出版社,2005.
[6]中华人民共和国电力行业标准.DL 5108-1999混凝土重力坝设计规范[S].北京:中国电力出版社,2000.
[7]长江勘测规划设计研究有限责任公司.嘉陵江亭子口水利枢纽初步设计报告[R].武汉:长江勘测规划设计研究有限责任公司,2009.
