用3D画板优化蚂蚁爬行最短路线的课件制作

2011-08-28唐剑岚

中小学电教 2011年11期

☆宗晓唐剑岚

（广西师范大学数学科学学院，广西桂林 541004）

立体几何中的“蚂蚁爬行最短路线”是个经典问题，该课件的制作方法多样，但是纵观各种方法，皆是在二维的平面上解决问题，这样制作的图形缺乏立体感，教师不易操作，学生不易观看，而且方法原理复杂，学生不易理解。运用3D几何画板优化蚂蚁爬行最短路线的课件制作，操作便捷，原理简单，立体视觉化效果好。本文将通过蚂蚁爬行圆锥体这个案例来说明运用3D几何画板优化蚂蚁爬行最短路线课件的制作。

案例（如图1）：在一个有盖的圆锥形的纸杯的杯口点A处有一只蚂蚁，它的家在圆锥的侧面某点F处，求蚂蚁沿纸杯表面爬行回家的最短距离？

图1

一、题意分析

蚂蚁沿着圆锥表面爬行回家有多种路线，总结分为两大类：沿着圆锥侧面和沿着圆锥的底面。根据两点之间线段最短的原理，这两大类中，最短路线分别是路线1：｜AF｜，路线 2：｜AE｜＋｜EF｜，其中｜AF｜为平面截圆锥侧面的轨迹（如图2）。

二、制作步骤

1.制作圆锥

利用【3d基本工具】｜【正交视图定点】，在正交视图中构造圆锥底面圆心center″及点Z作为圆周上的一点，构造圆。构造正交视图中圆center″圆周上的点Y；选中点Y和三维坐标系中的点Y，构造【轨迹】。在正交视图中构造圆锥顶点C。选择三维坐标系中的线段CY和正交视图中的点Y，构造【轨迹】。隐藏点Y、Z和线段CY。

2.制作圆锥体侧面上的轨迹

（1）在正交视图中圆 center″上构造 3点 A、D、E，以及弧AE和弧上点B；构造弧AB及弧上的点G。在三维坐标系中，连接线段 CA、CD、CE、CG，运用【3d基本工具】｜【线段上的定点】，构造线段CE、CD上的点F、H。

（2）作【直线】FH，ED，交于点 I；作【直线】FA，EA，EG。连接点 I、A，交直线 EG 于点 J；连接 FJ，交线段CG于点K。选中点K和正交视图中的点G，构造【轨迹】。隐藏线段CD、所有直线及直线的交点。

（3）在正交视图中，构造弧AG，并且其上的点L；连接三维视图中的线段CL，选中CL和正交视图中的点L，构造【轨迹】。将正交视图中的点G、L与点B重合，分别【右键】｜【属性】，取消【可以被选中】和【显示标签】。

（4）在正交视图中构造【移动按钮B→E】和【移动按钮B→A】，命为“圆锥侧面展开”和“圆锥侧面恢复”。

3.计算圆锥的侧面展开图圆心角

在正交视图中【度量】弧AE和【度量】弧AB。运用【3d基本工具】｜【获取点的坐标】得到点E、C两点的空间坐标；通过空间两点间距离公式，【计算】｜母线EC｜。利用圆锥的侧面展开图的圆心角公式：锥的侧面展开图。【计算】｜CF｜，【计算】利用【缩放】｜缩放比例，构造点 F，【度量】｜AF｜。隐藏×1弧度，【计算】圆锥侧面展开的圆心角度数和圆锥侧面展开到母线CE处的圆心角度数。

4.制作圆锥侧面展开图

（1）在界面的空白处构造一点C，【平移（｜EC｜/－90°）】得到点A；将线段AC以C为圆心，【旋转（侧面展开图的圆心角）】得到点B，【旋转（母线处的圆心角度数）】到点E，【构造（扇形CAB）】，扇形CAB即是圆圆锥侧面展开图。

（2）按照在空白处构造圆锥侧面展开图的方法，在圆锥上以线段CA为起点，做圆锥的侧面展开。

5.蚂蚁爬行路线

（1）在三维坐标系中计算｜AE｜、｜EF｜。路线 1：｜AF｜，路线 2：｜AE｜＋｜EF｜，并用不同的颜色标注出。

6.制作按钮，美化界面

制作路线 1、2的【显示/隐藏】按钮，命为路线 1、2，两条路线、长度和按钮路线1、2的总的【显示/隐藏】按钮，命为蚂蚁爬行路线。把不必要出现的地方隐藏。

最后的效果如图2：

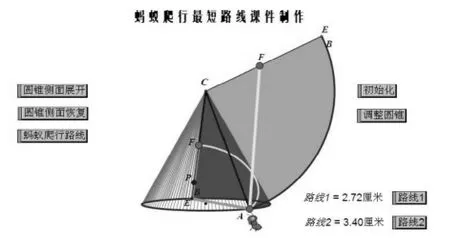
图2

三、课件操作

在操作课件时，通过按钮路线1、2直观地展示两条路线。移动线段CE上的点F来变化路线1、2的长度，其中点P是分界点，点F在线段CP上时，路线1最短，点F在线段PE上时，路线2最短。教师可以操控圆锥侧面展开/恢复按钮来展示侧面展开的过程，还可以手动拖动正交视图上的点B，动态展示圆锥的侧面展开过程，圆锥底面圆展开的弧长等于扇形的周长等。此外，通过操控扇形滑竿，可以从不同角度来观看圆锥的侧面展开。这样操作，突出教学重点和突破难点，有助于学生空间想象力的培养。