不损伤桥面更换拱桥吊杆的方法研究

王 欣 虞根淼 俞 峰

（1 兰州交通大学铁道技术学院，甘肃 兰州 730000；2 浙江正方交通建设有限公司，浙江 金华 321000）

1 引言

吊杆是中、下承式拱桥的重要构件，一般为高强钢丝或钢绞线外包防护PE组成的柔性索体。目前吊杆索体的设计年限一般约20年，但由于桥梁运营期间的超载、缺乏管养等，往往难以达到预期年限[1]。如1990年建成的四川宜宾小南门大桥在2001年11 月7 日曾出现吊杆突然断裂，桥面掉入河中，发生车毁人亡的惨剧，因而更换吊杆是这类桥梁维护的重要工作[2]。

目前，国内有几座吊杆拱桥对吊杆进行了更换，对吊杆更换技术做了一些尝试，但其方法都难以做到更换过程中维持桥面的完整。本文结合浙江省新昌县城西大桥加固改造工程对不损伤桥面更换拱桥吊杆的高要求，对不损伤桥面更换拱桥吊杆的方法进行了研究，提出一种在吊杆更换过程中保证桥面铺装不开裂的施工控制方法，实现了拱桥吊杆桥面无损更换。

2 吊杆更换过程中桥面铺装开裂分析

桥面铺装的作用是保护桥面板防止车轮或履带直接磨耗，保护主梁免受雨水侵蚀，并借以分散车轮的集中荷载。桥面铺装形成后，有一定的铺装厚度和刚度，因此会形成桥面结构连续[3]。

在吊杆更换过程中，存在吊杆力转换问题，导致该吊杆甚至相邻吊杆产生变形，从而使桥面标高上下变化。由于桥面铺装结构连续，相临吊杆之间标高变化会使桥面铺装受力，如果控制不当，会导致桥面开裂。

下面结合在吊杆更换过程中桥面标高发生变化的阶段，具体分析确定桥面铺装开裂发生的阶段以及破坏形式，为研究桥面无损更换提供依据。

阶段Ⅰ：在将原吊杆力转移到临时吊杆上时，临时吊杆逐级缓慢加载，该吊杆处横梁产生与临近横梁向上的相对位移，从而使桥面铺装在该横梁处产生转角θ。首先，桥面铺装在横梁处连续，致使其在该吊杆处产生负弯矩；其次，桥面铺装与桥面板具有粘结力，使该吊杆处一定长度范围的桥面铺装受拉。再次，对于桥面板简支的结构形式，如果相邻两孔变形不协调，桥面铺装还要承受桥面板端部提供的剪力。因此，在这个阶段桥面铺装主要是受弯，受拉，受剪破坏；当转角θ大于桥面开裂临界转角时，桥面铺装会沿横梁方向开裂。因此，必须通过设计施工控制桥面铺装的转角θ。

阶段Ⅱ：在临时吊杆按本级荷载张拉完成之后，切断原吊杆相应荷载比例的钢丝时，该吊杆处横梁在阶段Ⅰ的基础上产生向下的相对位移，桥面铺装转角θ慢慢减小。由于原吊杆与临时吊杆共同承受切断吊杆截面的荷载，因此该相对位移的大小与临时吊杆截面有关。若θ＞0，该吊杆处桥面铺装受力同阶段Ⅰ类似，并且铺装产生的转角数值较阶段Ⅰ小，不会引起桥面开裂；若θ=0，该吊杆处桥面铺装回到初始应力状态，不会引起桥面开裂；若θ＜0，该吊杆处桥面铺装产生负转角，结构受压，同样不会产生开裂。但是相临吊杆处桥面铺装产生正转角，其受力与阶段Ⅰ类似，如果向下相对位移过大，使相临吊杆处桥面铺装产生的转角大于桥面开裂临界转角，则桥面铺装会产生开裂。因此，必须控制向下相对位移的数值。由于该位移值的大小与临时吊杆截面有关，在设计时一般适当增大临时吊杆截面，有效控制该位移的大小，因此在阶段Ⅱ桥面铺装一般不会开裂。

阶段Ⅲ：当原吊杆完全拆除，逐步张拉新吊杆，并同时放松临时吊杆时，桥面标高会逐渐调整到初始标高，前期积累的相对位移值会慢慢恢复，桥面铺装转角会逐渐减小，应力逐渐降低，并最终回到初始状态。因此，在本阶段桥面铺装不会开裂。

综合上述分析，桥面无损更换的关键就是控制在阶段Ⅰ更换该吊杆处桥面铺装产生的转角θ。在更换吊杆过程中，若将θ控制在容许范围之内，桥面铺装就不会产生开裂。

3 桥面无损更换控制条件研究方法

由于在更换吊杆之前，桥面铺装已经投入使用，经过活荷载的反复作用产生了一定的变形、磨损，桥面铺装与桥面板的粘结力有所降低。桥面铺装的结构性能与设计值有了一定的差距，很难确定桥面铺装现状，精确计算出桥面开裂时的临界转角值。

依据对桥面铺装开裂分析，为了实现桥面无损更换，可以寻求一个在保证桥面不开裂时转角[θ]，以此作为控制条件进行吊杆更换设计与施工。该转角不宜过大，应与桥面开裂临界转角有一些的差距，使桥面铺装具有一定的安全系数，保证桥面不开裂。该转角也不宜太小，因为该转角是由临时吊杆按吊杆力分级加载的产生的，如果太小，会导致临时吊杆分级加载次数增加，使吊杆力转移效率降低，延长工期，造成浪费。为了合理确定桥面无损更换控制条件[θ]，引入如下假设：

(1)桥梁各部分材料处于弹性工作阶段。

(2)在设计荷载作用下，桥面铺装不发生开裂。

(3)在吊杆更换施工前，桥面铺装处于无应力状态。

(4)在吊杆更换施工过程中，桥面铺装不承受活荷载作用。

根据以上假设，可以借助该桥设计荷载与桥面上产生的桥面变形来确定控制条件[θ]，从而保证了桥面铺装不开裂，实现桥面无损更换，并具有一定的安全系数。图1 为桥面铺装转角θ的计算图示。

图中Δ 为该控制截面处桥面位移，Δ1、Δ2为相临吊杆处桥面位移，L 为吊杆间距。由此可以得出桥面铺装转角θ的计算公式。

下面结合城西大桥加固改造工程具体研究控制条件[θ]的确定。

城西大桥桥梁全宽15.2m，横向布置为：2.0m 人 行 道+ 1.1m 拱 肋+ 9.0m 行 车 道+1.1m 拱肋+2.0m 人行道。拱肋为箱形断面，高1.8m，宽1.1m，顶、底板厚0.2m，腹板厚0.18m，拱肋每3.0m 设置一道0.3m 厚横隔板；吊杆横梁采用预应力结构，高0.90m，跨中宽0.5m；吊杆间距为3m；该桥原设计荷载等级为汽车－20 级，挂车－100，人群荷载为3.0kN/m2。2001年因为桥面破损，对桥梁进行了加固，重新铺筑了桥面，并增设伸缩缝。桥面铺装层厚度0.13m，钢筋直径8mm，间距为10cm×10cm。

通过对桥梁进行移动荷载加载，发现当挂车-100 前轮作用于1＃吊杆时，桥面铺装会产生最不利转角。图2 为加载图示。图3 给出了桥面铺装在该活载作用下产生位移的折线图。

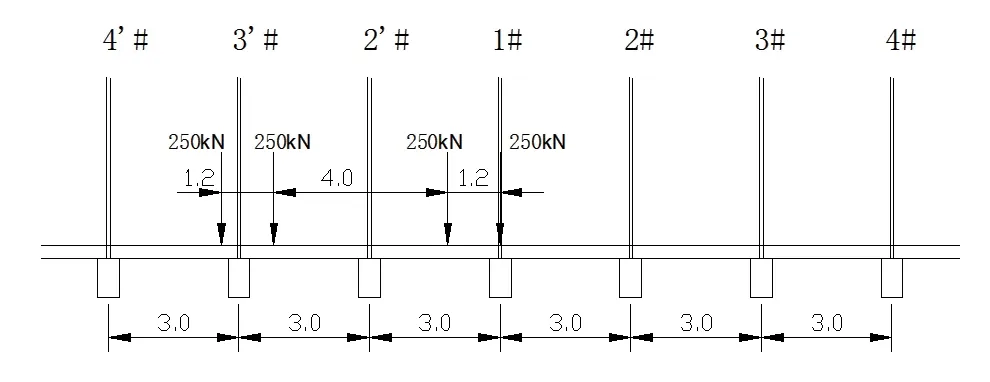
图2 桥面铺装产生最不利转角的加载图示

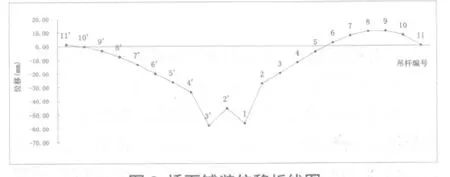
图3 桥面铺装位移折线图

由图3 可以看出，在2’＃、4’＃吊杆处桥面铺装转角较大，但是该吊杆附近桥面铺装作用于移动荷载，不能够反映在吊杆更换过程中桥面铺装受力状态，因此不作为制定控制条件依据。在2＃吊杆处桥面铺装在吊杆间距范围内没有移动荷载作用，其桥面铺装受力状态符合吊杆更换过程中的实际情况。因假设移动荷载作用时桥面铺装不开裂，所以2＃吊杆处桥面铺装产生的转角可以作为制定控制条件的依据。根据公式1，即可计算出保证桥面铺装不开裂时的转角[θ]。

4 桥面无损更换施工控制条件优化

要实现桥面无损更换，必须通过有效的施工控制来实现。根据前面分析的结果，得出了保证桥面不开裂时的控制转角[θ]。但是桥面转角在施工过程中测量困难，增大了施工控制难度，必须对控制条件进行优化。

由于桥面位移可以通过测量桥面标高得出，因此，若将控制桥面铺装转角转化为控制桥面标高变化，则会大大降低施工控制难度，确保桥面无损更换。

对公式1 进行变形，并代入保证桥面铺装不开裂的控制转角[θ]，可以得出更换吊杆处桥面标高变化与相临吊杆处桥面标高变化的关系。

吊杆处桥面标高变化与两个因素有关，即吊杆长度变形和拱肋标高变化。下面结合桥梁具体结构形式以及更换吊杆时的施工过程，分析更换吊杆处与相临吊杆处桥面标高的变化情况。

(1)在原吊杆力向临时吊杆转移的过程中，当临时吊杆缓慢加载，该吊杆力逐渐减小，吊杆长度变形减小。

(2)由于桥面板简支于吊杆横梁上，相临吊杆力变化取决于构成桥面连续的桥面铺装层，因此可以认为相临吊杆力变化很小。即便是变化，吊杆力也是减小的，吊杆长度变形减小。

(3)由于相临吊杆力变化很小，临时吊杆加载的力基本上等于该更换吊杆减少的力，并且拱肋截面抗弯惯性矩很大，因此拱肋标高变化很小，可以忽略。

基于上述分析，在临时吊杆缓慢加载的过程中，相临吊杆处桥面标高向上变化，并且产生的位移 Δ1、Δ2很小。因此，在施工过程中可以通过更换吊杆处桥面标高变化Δ 来控制。根据公式2 可知，忽略相临吊杆处桥面位移 Δ1、Δ2是偏于安全的。

至此得出桥面无损更换优化控制条件[Δ ]，其计算公式如下：根据前面对城西大桥计算分析结果，利用公式3 计算得出控制条件[Δ ]=10.78mm。在具体施工时，要求吊杆处桥面标高变化不能超过10mm。以此做为施工控制条件，城西大桥成功的完成了全部吊杆更换，并且桥面没有发生开裂，实现了桥面无损更换。

5 结语

本文就如何在拱桥吊杆更换过程中保证桥面不开裂进行了研究，主要得到以下结论：桥面铺装开裂主要发生在将原吊杆力转移到临时吊杆上，更换吊杆处桥面发生向上的位移时。如果控制不当，桥面铺装会沿横梁方向开裂，产生横向裂缝。通过分析得出了保证桥面不开裂时的控制转角[θ]，并对其进行优化，得到了桥面无损更换优化控制条件[Δ ]。结合城西大桥的相关背景，通过计算分析得出的控制桥面标高变化不超过10mm 来实现桥面无损更换，取得了良好的效果，证明了该方法是一个有效的施工控制方法，可以为同类工程提供参考。

[1]程华才，梅传江，赵永宽.吊杆拱桥吊杆更换拉锁工程的施工工艺[J].安徽建筑工业学院学报，2003,11：1-6

[2]李文琪,贺立新.对宜宾小南门桥事故的思考[J].中国公路,2002(22):47-48.

[3]马光述.桥面铺装层研究与应用国内外现状[J].价值工程.2010,1:62-63