具有MPPT功能的单级式光伏并网发电系统仿真分析

张 峥

(新疆电力设计院，新疆乌鲁木齐830002)

0 引言

光伏发电分为独立光伏系统和并网光伏系统，独立光伏系统电池费用占总费用的20%［2］，成本较高，而并网型光伏发电由于其造价低，输出电能稳定，具有广阔的发展前景［3］，也是未来发展的方向［4］。因此，本文建立了单级光伏并网系统电路，采用光伏阵列仿真模型进行了光伏发电系统仿真研究，使光伏系统输出电流相位跟踪电网电压相位满足并网要求，并在此基础上通过改变控制回路中电流大小实现了光伏阵列的最大功率跟踪。

1 单级光伏系统主电路拓扑

在光伏发电系统中，逆变器的性能是整个系统性能的关键，光伏系统可以分为单级式光伏系统和两级式光伏系统。传统的两级式系统由直流变换环节和逆变环节构成，功率点控制由直流变换环节完成，后者控制逆变及并网过程，虽然设计思路及实现相对简单，但环节较多，系统体积大，成本较高，转换效率较低。以1个能量变换环节实现并网的单级式系统只存在1级逆变结构，转换效率较高，拓扑结构简单［4－6］。光伏阵列是光伏发电系统的基础部件，其I－U，P－U特性受光照强度和工作环境温度的影响呈非线性关系。单级式单相光伏并网系统主电路结构如图1所示。它主要由光伏阵列 PV、直流侧平波电容 C1、VT1、VT2、VT3、VT4组成的双向全桥变换器和滤波环节组成。由于光伏阵列的伏安特性曲线是1个非线性曲线，因此光伏系统需要完成的2个最主要的功能就是光伏阵列的最大功率点的跟踪和并网跟踪。

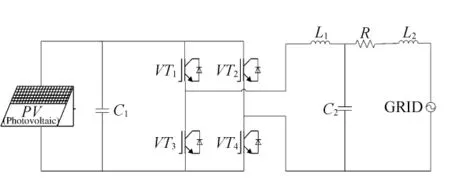
图1 单级光伏并网系统主电路结构

2 MPPT算法的比较

光伏阵列的输出特性是1个非线性曲线，其输出功率随光照和温度的变化而变化，而且在某个特定条件下其输出功率只在特定电压下保持最大功率，其输出I－U，P－U特性曲线呈非线性变化，需要在光伏控制系统中实现其最大功率的跟踪(MPPT)，保证其输出功率随光照和温度的变化而始终工作在最大功率点附近。现在主要采用的光伏阵列跟踪功率方法主要有恒电压跟踪法和最大功率跟踪方法。由于恒电压跟踪(CVT)法光伏阵列的输出电压固定在某个恒定值，光伏阵列的最大功率点摆动幅度不大，但在外界条件变化过多的情况下 CVT法将损失过多的功率，影响系统的效率［7］，因此现在更多采用MPPT方法。

2.1 光伏模型

基于matlab/simulink的光伏阵列模型主要根据数学模型建立光伏阵列模型［8］，其光伏阵列V－I输出特性的表达式为

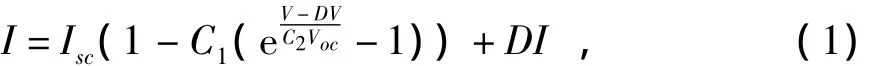
式中:Isc为短路电流;Voc为开路电压。

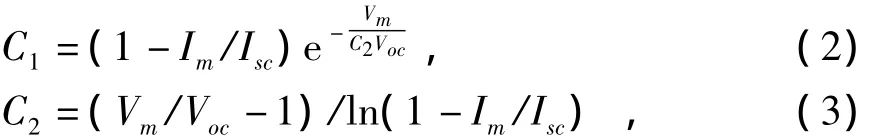
式中:Im为最大功率点电流;Vm为最大功率点电压;DI、DV分别为太阳光照辐射和温度影响参数，由光照和温度变化系数决定。

2.2 MPPT 算法

最大功率跟踪算法主要包括扰动观察法(P＆O)和导纳增量法(IncCond)以及由此改良的各种算法，其它还有短路电流法(SC)、寄生电容法(PC)、线性电流法(LC)和各种模糊控制方法［9］。扰动观察法原理比较简单，即不断的扰动电压使电压变化同时检测功率变化的方向，如果功率减小则反向扰动，否则同向继续扰动。由于这种方法需要不断的扰动电压，所以阵列输出功率会在最大功率点附近反复震荡，并有可能产生误判断。导纳增量法是根据光伏阵列最大功率点处功率对电压的导数为零的条件来进行最大功率点判断的。若电压变化量为零，电流变化量大于零，减小给定电压的幅值，反之则增大。若电压变化量不为零，则判断输出电导的变化量是否等于输出电导的负值;若电导变化量大于负电导值，减小给定电压的幅值，反之则增大幅值。该方法理论上能避免扰动观察法稳定条件下功率震荡的问题。其判断条件为［10］

导纳增量法精确度最高，由此衍生出了多种改进方法，其缺点为算法比较复杂，硬件质量要求比较高，运算时间较长，应用性得到了一定的限制。

3 系统控制策略及其过程

典型的光伏系统逆变器多数采用电压源逆变电路结构，与电网之间有缓冲电感，逆变器输出电流和输出电压之间有1个很小的夹角，输出一定的无功。逆变器输出的有功功率大小由MPPT控制。系统的控制目标是使逆变器输出电流的相位和电网电压相位保持一致，输出功率达到光伏阵列在此时刻的最大输出功率。

逆变器输出功率为

式中:USM为并网电压幅值;ISM为并网电流幅值;θ为电网电压与并网电流间的相位差。通过式(1)可知，并网电流可以被调制成与电网电压同相的正弦波，实现系统的功率因数为1。而调整ISM就可以调整逆变器的输出功率，从而可以实现最大功率的跟踪。光伏并网系统的控制框图如图2所示。

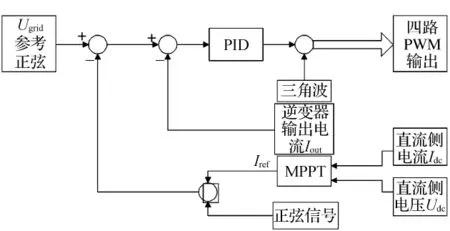
图2 光伏并网系统的控制框图

在图2中，逆变器输出电流反馈到控制主回路，与参考正弦比较后，调节输出电流的相位，控制功率因数。若直流侧功率小于最大输出功率，则增加逆变器输出电流，反之则减小。最后通过与三角波比较得到四路PWM输出。

4 系统仿真及其结果

依据上述的控制方法及主电路结构，本文利用Matlab2008b/simulink搭建了单级光伏逆变系统仿真模型，如图3所示。

在图3中，光伏阵列开路电压为430 V，短路电流为10.65 A。标准温度为28℃、标准光照为1 kW/m2时，光伏阵列最大功率点电压为400 V，最大功率点电流为10.25 A。L、C1为逆变输出滤波装置，C为直流侧电容。由于仿真中存在电网电流回馈影响直流侧电流，由此检测到的直流侧功率会失真，无法进行准确的最大功率点跟踪。所以，在光伏阵列和逆变器之间应增加抗干扰环节，才能保证MPPT输入端电流的准确。

在光照变化条件下，应用此系统进行光伏阵列并网实验，初始条件:温度为25℃，光照为0.6 kW/m2。在运行到 0.5 s时，光照突变为 1.2 kW/m2。由直流侧输出功率可以看出，光照变化后功率能够上升到光伏阵列的最大输出功率。输出电流的相位基本能够跟踪电网电压的相位，输出电流的幅值能够随着光照的升高而升高。系统可以实现并网电流与电网电压的相位跟踪，并通过改变并往电流的大小改变光伏阵列的输出功率，达到最大功率跟踪的目的，图4为系统的输出结果。

从图4中可以看到，在光伏阵列输出功率改变的情况下，系统输出的无功功率并没有显著的变化，这说明系统并网的相位跟踪是稳定的。

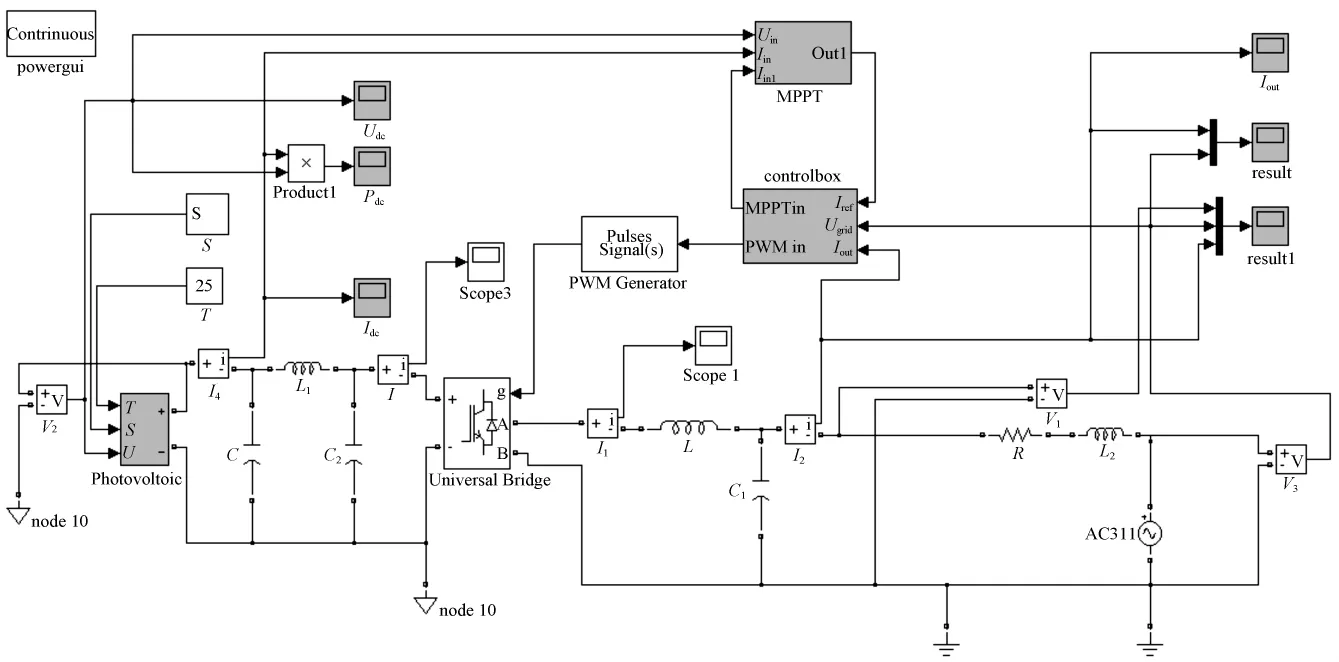
图3 系统仿真模型

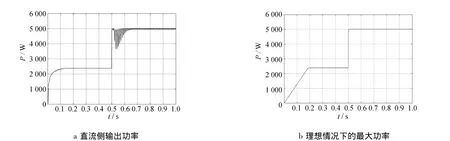
图4 系统的输出结果

5 结论

具有MPPT功能的单级式光伏并网发电系统仿真实验表明，利用Matlab2008b/Simulink建立光伏阵列模型和光伏并网系统，并网效果良好，能在外界环境改变的情况下及时调整光伏阵列的输出功率达到最大功率点，保持系统稳定。

［1］张国荣，张铁良，丁明，等.光伏并网发电与有源电力滤波器的统一控制［J］.电力系统自动化，2007，31(8):61－66.

［2］Yi Huang，Fang Z.Peng，Jin Wang，Dong－wook Yoo.Survey of the Power Conditioning System for PV Power Generation［A］.Power Electronics Specialists Conference［C］，2006.PESC ’06.37th IEEE.

［3］张超，王章权，蒋燕君.无差拍控制在光伏并网发电系统中的应用［J］.电力电子技术，2007，41(7):3 －5.

［4］王斯成，余世杰.3k可调度型并网逆变器的研制［J］.太阳能学报，2001，22(1):17－20.

［5］刘树，刘建政，赵争鸣，等.基于改进MPPT算法的单级式光伏并网系统［J］.清华大学学报(自然科学版)，2005，45(7):873－876.

［6］Zue A O，Chandra A.Simulation and stability analysis of a 100 kW grid connected LCL pho tovoltaic inverter for industry［C］//IEEE Power Engineering Society General Meeting，Montreal，Canada，2006:1 －6.

［7］赵争鸣，刘建政，孙晓瑛，等.太阳能光伏发电及其应用［M］.北京:科学出版社，2005:233 －244、116.

［8］茆美琴，余世杰，苏建徽.带有MPPT功能的光伏阵列Matlab通用仿真模型［J］.系统仿真学报，2005，17(5):1248 －1251.

［9］李晶，窦伟，徐正国，等.光伏发电系统中最大功率点跟踪算法的研究［J］.太阳能学报，2007，28(3):268 －273.

［10］叶满园，官二勇，宋平岗.以电导增量法实现MPPT的单级光伏并网逆变器［J］.电力电子技术，2006，40(2):30 －32.